Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1305

.pdf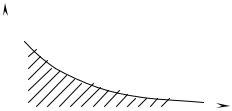

Скачиваний:

Добавлен:

30.04.2022

Размер:

953.53 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 136 7 8 9 10 11 12 13 > Следующая >>>

Если указанный предел существует, то несобственный интеграл называется сходящимся. Если предел не существует или бесконечен, то несобственный интеграл называется расхо-

дящимся.

Пример 2.7.1. Вычислить несобственный интеграл +∞∫ dx.

1 x2

Решение:

+∞dx

lim

b dx

lim

= lim

−

+1 =1.

b→+∞

∫

b→+∞

Несобственный интеграл сходится.

Пример 2.7.2

Вычислить

несобственный

интеграл

+∞

xdx

∫1

x2 +1

Решение:

+∞

xdx

= lim

∫1

x2 +

b→+∞ ∫1

x2 +1

b→+∞

=1 lim (ln(b2 +1)−ln 2)= ∞.

2 b→+∞

Предел равен бесконечности, следовательно, интеграл расходится.

Геометрическая интерпретация сходящегося несобствен-
ного интеграла при			f (x)≥ 0 - площадь бесконечно длинной
криволинейной трапеции (рис 4).
	y		y = f (x)
	y



	O	a	x
	O	a	x
			Рис. 4
			50

Большинство свойств определённого интеграла (кроме оценки и теоремы о среднем) для несобственных интегралов сохраняются.

Если f(x) непрерывна на промежутке (−∞,b], то аналогичным образом может быть определен несобственный интеграл первого рода на промежутке (−∞,b]:

∫b	f (x)dx = alim→−∞ ∫b	f (x)dx .
−∞	N

Если f(x) непрерывна на всей числовой оси, то

∞	f (x)dx =	lim	c	f (x)dx +	lim	M	f (x)dx .
∫			∫			∫
−∞		N→−∞ N			M →∞ c

∞

В этом случае интеграл ∫ f (x)dx сходится, если сходятся

−∞

оба интеграла в правой части.

2.8. Несобственные интегралы второго рода

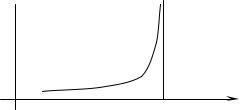
Пусть функция f (x) определена и непрерывна на промежутке[a,b), а в точке b терпит разрыв II рода (рис. 5).

y = f (x)

O a

Рис. 5

b−ε

Тогда, если существует конечный предел lim ∫ f (x)dx ,

ε→0 a

( ε >0), то его называют несобственным интегралом второго

рода и обозначают ∫ f (x)dx . Если предел не существует или

бесконечен, то несобственный интеграл второго рода называется расходящимся.

Аналогично определяется интеграл с особенностью подынтегральной функции на нижнем пределе. Пусть f (x) не-

прерывна на промежутке (a,b], а при x = a имеет разрыв II рода, тогда

b		b
∫ f (x)dx =	εlim→0	∫ f (x)dx.
a		a+ε

Если функция y = f (x) испытывает разрыв второго рода во внутренней точке c отрезка [a,b], то несобственный интеграл второго рода определяется формулой

b			c−ε			b	f (x)dx .
∫	f (x)dx =	lim	∫	f (x)dx +	lim	∫	f (x)dx .
a		ε→0	a		ε→0 c+ε

Несобственный интеграл слева сходится, если сходятся каждый из несобственных интегралов, расположенных справа.

Если f (x)≥ 0 , то несобственный интеграл второго рода

∫ f (x)dx интерпретируется геометрически как площадь беско-

нечно высокой криволинейной трапеции.

∫1

Пример 2.8.1. Вычислить несобственный интеграл

dx . 1− x

Решение:

= lim

∫b

= − lim 2

= lim 2(

−1)= 2 .

1− x

1−b

1− x

b→1−0

1− x

b→1−0

Вопросы для самопроверки

1.Сформулируйте определение определенного интеграла.

2.Каков геометрический смысл определенного интегра-

ла?

3. Что является достаточным условием интегрируемости функции?

4. Перечислите свойства определенного интеграла.

5. Выведите формулу Ньютона – Лейбница.

6. Как производится замена переменной в определенном интеграле?

7.Формула интегрирования по частям.

8. Что собой представляет несобственный интеграл первого рода?

9. Дайте определение несобственного интеграла второго

рода.

10. Каков геометрический смысл несобственных интегралов первого и второго рода?

Задачи для самастоятельного решения

Вычислить определенные интегралы

1	xdx		1 ).
1. ∫	xdx	(Ответ:
1. ∫	2	(Ответ:
0	(x2 +1)		4

2. ∫ln2 xdx (Ответ: e − 2 ).

1 e

3.	∫		dx		(Ответ:		π ).
3.	∫				(Ответ:		π ).
	1	x	1−ln2	x			2
	1
	1	1	+ x dx			π		3
4.	∫	1		(Ответ:		π	+1−	3	).
4.	∫	1		(Ответ:		6	+1−		).
	0	1	− x			6		2
	0
							53

	4			xdx
	4												(Ответ: 3							2 ).
5.	∫
5.	∫
	1			2 + 4x														2
	π							dx											π
6.	∫							dx						(Ответ:					π						).
			3 + 2cos x
																				5
	0																			5
	π																							2 ).
7.	∫sin x cos2 xdx (Ответ:																							2 ).
	0																							3
	0
	π
8.	∫2 sin3 xdx (Ответ: 2 −																			π ).
	0																			2
	0

		3																π
9.	∫arctgxdx (Ответ:																	π					−ln 2).

																		3
	0																	3
		1																e2 −5 ).
10.			∫x2e−x dx											(Ответ:				e2 −5 ).
		−1																			e
		−1
		2							dx													π ).
11.		∫							dx							(Ответ:
11.		∫			2											(Ответ:
		1 x						− 4x +5														4
		2
		2				x2 −1 dx																					− π ).
12. ∫															(Ответ:
																								3
																								3
		1								x														3
		1
		0								dx
13.			∫							dx							(Ответ: ln 2 ).
13.			∫														(Ответ: ln 2 ).
		−2					x2 + 2x +9
		π
		∫4						dx																		arctg			).
14.														(Ответ:								2
																						2						2
												2																2
		0 1+sin											x							2
		π								x								5π ).
15.		∫sin6								x	dx			(Ответ:
15.		∫sin6							2		dx			(Ответ:
		0							2									16
		0
																						54

π2 sin 1

16. ∫ 2x dx (Ответ: 1).

0π1 x

Вычислить несобственные интегралы

	∞	(x2 dx+ 49) (Ответ:		π
17.	∫0			π	).
17.	∫0			14	).
	∞		1 ).
18.	∫e−3x dx (Ответ:		1 ).
	0		3
	0

∞ dx

19.∫1 x2 + x (Ответ: ln 2 ).

20.∞∫1+xln x dx (Ответ: интеграл расходится).

21. ∫		xdx	(Ответ: 1).

	1− x2
0	1− x2

1 ln xdx

22.∫ x2 (Ответ: 1).0

3. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

3.1. Площадь плоской фигуры в декартовых координатах

Если	f (x) ≥ 0	на отрезке [a,b], то площадь криволиней-
ной трапеции вычисляют по формуле
			b
		S = ∫ f (x)dx.
			a
Если	f (x) ≤ 0	на [a,b], то
		S = −∫b	f (x)dx = ∫b	f (x)	dx .
				f (x)	dx .

		a	a

Если f(x) принимает на [a,b] значения разных знаков, то

S = ∫ f (x) dx

Пример 3.1.1. Вычислить площадь фигуры, ограниченной линиями: y = x2x+1, y = 0, x =1, x = 3 (рис. 6).

Решение:

xdx

1ln(x2

+1)

(ln10 −ln 2)=

1 ln 5.

S = ∫

x +

y =

2 +1

			x
O	1 x	3	x

Рис. 6

Площадь фигуры, ограниченной линиями		y =ϕ1 (x),
y =ϕ2 (x), x = a , x = b ,	если выполняется	условие
ϕ2 (x)>ϕ1 (x), может быть вычислена по формуле:
b
S = ∫(ϕ2	(x)−ϕ1 (x))dx.

Пример 3.1.2. Вычислить площадь фигуры, ограниченной линиями y = x2 −3x − 4, y = x +1. (рис. 7).

Решение:

y y = x +1

-1 0	5	x
y = x2
	−3x − 4

Рис. 7

Для нахождения абсцисс концов отрезка интегрирования приравняем y = x2 −3x − 4 и y = x +1. В результате получаем

квадратное уравнение x2 − 4x −5 = 0 ,										решая которое находим
x1 = −1 и x2	= 5 . Тогда
5			5	(− x									x3				5
5			5
S = ∫(x +1−(x	2	−3x − 4))dx = ∫					2								2
	2						2	+			−			+ 2x	2			=
								+	4x +5)dx =		−	3		+ 2x		+5x	−1	=
−1			−1									3					−1
= −	125		+50 + 25 −		1	+ 2				= −42 +		78		= 36 .
= −		3	+50 + 25 −		3	+ 2			−5	= −42 +		78		= 36 .
		3			3
						57

3.2. Площадь фигуры, ограниченной кривой, заданной параметрическими уравнениями

Рассмотрим случай, когда криволинейная трапеция ограничена кривой, заданной уравнениями в параметрическом виде:

x =ϕ(x)	, t1 ≤ t ≤ t2 , прямыми x = a и x = b и осью Ox ,
	, t1 ≤ t ≤ t2 , прямыми x = a и x = b и осью Ox ,
y =ψ(x)
где ϕ(t1 ) = a,	ϕ(t2 ) = b .
Формулу для вычисления площади криволинейной тра-
	b

пеции можно получить из формулы S = ∫ ydx , выполнив заме-

ну переменной x =ϕ(x),				a
				′
		dx =ϕ (t)dt, y =ψ(t):
			t2
	S = ∫ψ(t)ϕ′(t)dt .
			t1
Пример 3.2.3. Вычислить площадь фигуры, ограничен-
	x = a cost	,	0 ≤ t ≤ 2π .
ной эллипсом		,	0 ≤ t ≤ 2π .
	y = bsin t
Решение:
Вычислим четверть площади эллипса,						когда x меняется
от 0 до a , в то время как t			меняется от π		до	0 .
			2
			y
			b
					t	= 0
			O		a		x
					a

		Рис. 8
			58

											π
1 S =	a	0					0
1 S =	∫ydx =	∫bsin t(a cost)′dt = −∫absin2 tdt = ab∫2 sin2 tdt =
4	0	π					π				0
	0	π					π				0
		2					2
π						π
2	1−cos 2t			ab	sin 2t	π		ab π			πab
2	1−cos 2t		dt =	ab	sin 2t	2	=	ab π	−0	=	πab	,	S =πab.
= ab∫	2		dt =	t −	2		=		−0	=	4	,	S =πab.
0	2			2	2	0		2 2			4
0						0

3.3. Площадь криволинейного сектора в полярной системе координат

Полярная система координат образуются точкой O , называемой полюсом, полярной осью, представляющей собой луч, выходящий из полюса. Произвольная точка на плоскости характеризуется полярным радиусом ρ , равным расстоянию

от полюса O до точки, а также полярным углом ϕ . Полярный

угол отсчитывается от полярной оси против часовой стрелки и меняется в пределах от 0 до 2π .

Для выяснения связи полярных и декартовых координат совместим с полюсом начало системы декартовых координат, а ось Ox - с полярной осью (рис.9). Рассмотрим точку M ,

имеющую декартовы координаты (x, y) и полярные координаты (ρ,ϕ).

Из треугольника на рис. 9 следуют формулы перехода от полярных координат к декартовым координатам и наоборот:


x = ρ cosϕ,	ρ =	x2 + y2 ,
y = ρsinϕ,	tgϕ =	y	.

		x

<<< < Предыдущая 1 2 3 4 56 / 136 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022952.42 Кб2Учебное пособие 1300.pdf
#
30.04.2022952.61 Кб3Учебное пособие 1301.pdf
#
30.04.2022952.68 Кб5Учебное пособие 1302.pdf
#
30.04.2022953.4 Кб2Учебное пособие 1303.pdf
#
30.04.2022953.41 Кб2Учебное пособие 1304.pdf
#
30.04.2022953.53 Кб4Учебное пособие 1305.pdf
#
30.04.2022953.58 Кб1Учебное пособие 1306.pdf
#
30.04.2022955.36 Кб2Учебное пособие 1307.pdf
#
30.04.2022957.09 Кб6Учебное пособие 1308.pdf
#
30.04.2022958.63 Кб4Учебное пособие 1309.pdf
#
30.04.2022292.6 Кб1Учебное пособие 131.pdf