
Линейная алгебра. метод. указания и контрольные задания по курсу математики. Акчурина Л.В., Колпачев В.Н
.pdfМинистерство образования и науки РФ
Государственное образовательное учреждение высшего профессионального образования
Воронежский государственный архитектурно-строительный университет
ЛИНЕЙНАЯ АЛГЕБРА
Методические указания и контрольные задания по курсу математики
Воронеж 2011
2
УДК 51.07
Составители Л.В. Акчурина, В.Н. Колпачев, Е.И. Ханкин, С.В. Артыщенко
Линейная алгебра: метод. указания и контрольные задания по курсу математики / Воронеж. гос. арх.-строит. ун-т; сост.: Л.В. Акчурина, В.Н. Колпачев, Е.И. Ханкин, С.В. Артыщенко
– Воронеж, 2011. – 54 с.
Методические указания содержат краткие теоретические сведения по операциям с матрицами и решению систем линейных уравнений, нахождению собственных чисел и собственных векторов линейных преобразований, решение типовых задач, а также индивидуальных заданий для студентов очной формы обучения. Приведены 28 вариантов заданий.
Предназначены для студентов всех специальностей. Ил. 1. Библиогр.: 5 назв.
УДК 51.07
Печатается по решению редакционно-издательского совета Воронежского государственного архитектурно-строительного университета
Рецензент – В.П. Авдеев, д.т.н., проф. кафедры математического моделирования и вычислительной техники Воронежского государственного архи- тектурно-строительного университета
3
Введение
В последние годы все больше возрастает роль линейной алгебры в различных разделах математики и техники. При изучении студентами строительных специальностей таких дисциплин как строительная механика, строительные конструкции, теплотехника, математическое моделирование и др., существенно используются линейные преобразование и действия над матрицами.
Настоящие методические указания предназначены для того, чтобы помочь студенту всех форм обучения овладеть приемами и методами решения задач по теме: “Линейная алгебра”, а также обеспечить самостоятельность выполнения контрольных работ. Характер и объём заданий подходит как для аудиторной, так и внеаудиторной самостоятельной работы студентов.
Материал методических указаний содержит:
1.Краткие теоретические сведения;
2.Решения типовых задач;
3.Варианты контрольных заданий.
Студенту перед каждым практическим заданием рекомендуется:
1.Изучить по учебнику и по конспекту лекций теоретический материал по соответствующему разделу темы “Линейная алгебра”;
2.Запомнить теоретические сведения (определения, формулы, теоремы), разобрать решения типовых примеров и, по возможности, самостоятельно воспроизвести эти решения.
4
1. ОПЕРАЦИИ НАД МАТРИЦАМИ Прямоугольная таблица из чисел аij (i 1,2,...m; j 1,2,...n ) вида
a |
a |
... |
a |
|
11 |
12 |
|
1n |
|
a21 |
a22 |
... |
a2n |
|
А = |
|
... |
... |
|
... ... |
|
|||
|
am 2 |
... |
|
|
am1 |
amn |
|||
состоящая из m строк и n столбцов, называется матрицей размера m n . Элемент матрицы аij располагается в i-ой строке и j -ом столбце. Строки и столб-
цы матрицы называются ее рядами. Под двумя параллельными рядами понимают две строки или два столбца матрицы.
|
a |
0 |
... |
0 |
|
|
1 |
0 |
... |
0 |
|
|
||
|
|
11 |
a22 |
... |
0 |
|
|
|
0 |
1 |
... |
0 |
|
|
Квадратные матрицы |
|
0 |
|
, |
|
|
называются диаго- |
|||||||
|
|
... |
... |
0 |
|
|
|
... |
... |
... |
|
|||
|
... |
|
|
... |
|
|
||||||||
|
|
0 |
0 |
... |
|
|
|
|
0 |
0 |
... |
1 |
|
|
|
|
ann |
|
|
|
|
||||||||
нальной и единичной E , соответственно.
Матрица, полученная из исходной путем замены каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной, и
|
|
|
|
a |
a |
21 |
... |
a |
m1 |
|
|
|
|
|
11 |
|
|
|
|
||
обозначается |
T |
: |
T |
a12 |
a22 |
... |
am2 |
|
||
A |
A |
= |
|
|
... ... |
. |
||||
|
|
|
|
... ... |
|
|||||
|
|
|
|
a |
a |
2n |
... |
a |
mn |
|
|
|
|
|
1n |
|
|
|
|
||
Суммой (разностью) матриц Am n aij и Bm n bij , имеющих одинаковые размеры, называется матрица Сm n сij , кого же размера что и исходные,
каждый элемент которой равен сумме (разности) соответствующих элементов матриц A и B : сij aij bij ( сij aij bij ), где i 1,2,...m; j 1,2,...n .
Произведением матрицы Am n aij на число называется матрица
Bm n bij такая, что bij aij , где i 1,2,...m; j 1,2,...n . Очевидно, что на числоможет быть умножена матрица произвольного размера.
Произведением матриц Am n aij и Bk p bij называется матрица Сm p сij , каждый элемент которой сij равен сумме произведений элементов i- ой строки матрицы A на соответствующие элементы j -ого столбца матрицы
n
B , т.е. сij ais bsj . Важно отметить, произведение матриц вводится лишь в
s 1
том случае, если количество столбцов первой из перемножаемых матриц равно количеству строк второй из перемножаемых матриц, т.е n k .
Матрицы A и B называются перестановочными, если A B B A .
|
|
|
|
|
|
|
|
|
5 |
|
k 1 квадратной матрицы A назы- |
||||
Целой положительной степенью Ak |
|||||||||||||||
вается произведение |
|
A A ... A. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
1 |
3 |
4 |
||
Пример 1. Даны матрицы А = |
2 |
1 |
4 |
; B = |
5 |
7 |
8 . |
||||||||
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
||||
Найти матрицу X , удовлетворяющую условию X 0,5 A B 0,5 . |
|||||||||||||||
Решение. Из условия X 0,5 A B 0,5 |
следует, что |
X 2A B . Согласно оп- |
|||||||||||||
ределению имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 4 6 |
|
1 3 |
4 |
3 7 10 |
|
|
|
|
|
||||||
|
4 2 8 |
|
|
5 7 |
8 |
|
|
9 9 16 |
|
|
|
|
|
||
X 2A B = |
|
+ |
|
= |
|
|
|
|
|
||||||
|
6 4 6 |
|
|
1 2 |
4 |
|
|
7 6 10 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Пример 2. |
Найти произведения |
AB , |
BA и |
ВС матриц А = |
4 , В = |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
||||
2 4 1 и С |
2 1 |
4 . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||
Решение. Согласно определению произведения матриц, имеем |
|
|||||||||||||||||
1 |
|
|
|
|
|
1 |
2 |
1 4 |
1 1 |
2 |
4 1 |
|
|
|||||
|
4 |
|
|
|
|
|
|
4 |
2 |
4 4 |
|
|
|
8 |
16 4 |
|
|
|
AB = |
2 |
4 1 = |
4 1 |
|
. |
|
|
|||||||||||
|
3 |
|
|
|
|
|
|
3 |
2 |
3 4 |
3 |
|
|
6 12 3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
BA = 2 |
4 |
1 |
4 |
= (2 1 + 4 4 + 1 3) = (2 + 16 + 3) =( 21). |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнивая результаты, замечаем, что в данном примере A B В A |
|
|||||||||||||||||
|
|
|
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|||
ВС = 2 |
|
|
2 1 |
|
4 |
|
|
|
|
|
|
2 2 4 1 1 2 |
2 3 4 4 1 3 = |
|
||||
4 1 |
|
= 2 1 4 2 1 3 |
|
|
||||||||||||||
|
|
|
|
3 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 13 10 |
25 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2. ОПРЕДЕЛИТЕЛИ, ИХ СВОЙСТВА И ВЫЧИСЛЕНИЕ |
|
||||||||||||||
Определение 1. Определителем n-го порядка, соответствующим квадрат- |
||||||||||||||||||
|
|
|
|
|
a |
|
a |
... |
a |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
11 |
|
|
12 |
|
1n |
|
|
|
|
|
|
|
ной матрице А = |
a21 |
|
a22 |
... |
a2n |
|
называется число, которое может быть вы- |
|||||||||||
|
|
|
... |
... |
... |
, |
||||||||||||
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
an1 |
|
an2 |
... |
ann |
|
|
|
|
|
|
|||
числено по элементам матрицы по формуле:
6
n
det A = ( 1)k 1 a1k M1k ,
k 1
где М1к – минор элемента a1k , полученный из исходной матрицы вычеркивани-
ем первой строки и k–го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Определение 1. Минором Мij элемента аij определителя n-го порядка на-
зывается определитель (n–1)-го порядка, получаемый вычеркиванием i-ой строки и j-го столбца, на пересечении которых стоит этот элемент.
Определение 2. Алгебраическим дополнением Аij элемента аij определи-
теля n-го порядка называется его минор, умноженный на 1 i j : Аij 1 i j Mij .
Например, для матрицы 2-го порядка
|
a11 |
a12 |
|
= ( 1)1 1 a M |
11 |
( 1) |
2 1 a M |
12 |
a M |
11 |
a M |
12 |
a a |
22 |
a a |
21 |
. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
a21 |
a22 |
|
|
|
11 |
|
|
|
12 |
|
|
|
11 |
|
|
12 |
|
|
11 |
|
12 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Например, для матрицы 3-го порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
a11 |
a13 |
|
a13 |
|
( 1)1 1 a M |
|
|
|
2 1 a M |
|
( 1)3 1 a M |
|
a M |
|
a M |
|
a M |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
a |
21 |
a |
22 |
|
a |
23 |
|
11 |
( 1) |
12 |
13 |
11 |
12 |
13 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
11 |
|
|
12 |
13 |
|
||||||||||||
|
a31 |
a32 |
|
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
a22 |
a23 |
|
a21 |
|
a23 |
|
a21 |
|
a23 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
= a |
a |
|
a |
|
|
= |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
11 |
a |
|
a |
|
|
12 |
a |
|
|
a |
13 |
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
33 |
|
|
|
31 |
|
|
33 |
|
31 |
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|||
a11a22a33 a13a21a32 a12a23a31 a12a21a33 a13a22a31 a11a23a32 .
Последняя формула вычисляет значение определителя разложением по первой строке. Можно написать такие же формулы для второй и третьей строки, а так же и для столбцов матрицы. Нужно отметить то, что при использовании этого правила для матрицы 4-го порядка миноры Мij будут детерминантами матриц 3-го порядка и т.д.
Замечание. Для вычисления определителя 3-го порядка может быть рекомендовано правило Саррюса (правило треугольника):
со знаком “+” берутся произведения элементов главной диагонали матрицы и элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали (это произведения a11a22 a33 , a13a21a32 , a12a23a31 -
они не меняют знака в сумме); со знаком “–” - три члена, расположенные аналогичным образом относи-
тельно побочной диагонали (это произведения a12 a21a33 , a13a22 a31 , a11a23a32 - они
меняют свой знак в сумме на противоположный). Схематически это правило изображается так:
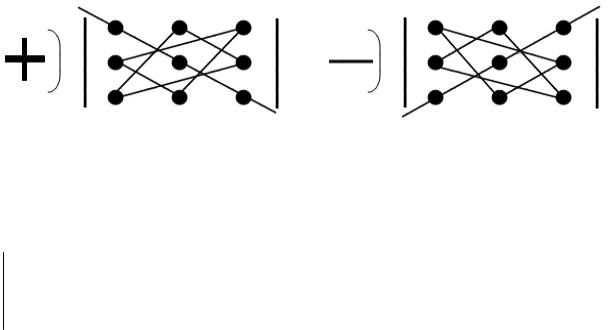
7
Рис. 1. Правило треугольника |
|
|
|
|
1 |
1 |
2 |
|
|
|
3 |
2 |
1 |
|
Пример 1. Вычислить определитель матрицы |
. |
|||
|
1 |
4 |
3 |
|
|
|
|||
1 |
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
2 |
|
1 |
|
2 |
1 |
|
1 |
|
3 |
1 |
|
2 |
|
3 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||
3 |
2 |
1 |
|
|
|
|
|
|
= –1(6 – 4) – 1(9 – 1) + 2(12 – 2) = 10. |
|||||||||
1 |
4 |
3 |
|
|
|
4 |
3 |
|
|
|
1 |
3 |
|
|
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Основные свойства определителей
1.Величина определителя не меняется при транспонировании.
2.Если в определителе переставить любые две строки (два столбца) местами, то значение определителя изменит знак на противоположный.
3.Общий множитель у всех элементов какой-нибудь строки (столбца) можно вынести за знак определителя.
4.Если определитель имеет две пропорциональные строки или два пропорциональных столбца, то он равен нулю.
Следствие 1. Если все элементы какой-либо строки (столбца) определителя равны нулю, то и определитель равен нулю.
Следствие 2. Если определитель имеет две одинаковые строки (два одинаковых столбца), то он равен нулю.
5.(Теорема о разложении определителя по строке). Определитель равен произведению элементов любой его строки (столбца) на их алгебраические дополнения.
6.Сумма произведений элементов какой-либо строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю.
7.Если все элементы какой-либо строки определителя представить в виде сумм двух чисел, то значение определителя будет равно сумме определителей, полученных из первоначального определителя заменой соответствующей строки на строки, состоящие из первых и вторых слагаемых, соответственно. Аналогичное правило справедливо и для столбцов определителя.
8.Значение определителя не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же произвольное число.
8
2.Основные методы вычисления определителей n-го порядка
1.Метод понижения порядка (разложение определителя по элементам ря-
да). Прежде чем применять метод понижения порядка, полезно, используя основные свойства определителей, обратить в нуль все, кроме одного, элементы его некоторой строки или столбца.
Пример. Вычислить определитель
|
1 |
2 |
0 |
3 |
|
|
|
|
|||||
|
2 |
5 |
1 |
4 |
|
. |
|
1 |
2 |
3 |
1 |
|
|
|
2 |
4 |
1 |
2 |
|
|
Решение. Применяя свойство 8, преобразуем определитель так, чтобы его 3-й столбец имел три нуля, например, за счет строчки 4. Для этого прибавим ко второй строке 4-ю, а к 3-ей строке прибавим 4-ю, умноженную на 3. Имеем:
|
1 |
2 |
0 |
3 |
|
1 |
2 |
0 |
3 |
|
|
|
|
||||||||
|
2 |
5 |
1 |
4 |
|
4 |
9 |
0 |
6 |
|
|
1 |
2 |
3 |
1 |
|
7 |
14 |
0 |
7 |
|
|
2 |
4 |
1 |
2 |
|
2 |
4 |
1 |
2 |
|
Применим формулу разложения определителя по 3-ему столбцу |
||||||||||
a13 A13 a23 A23 a33 A33 a43 A43 0 A13 0 A23 0 A33 ( 1) A43 |
||||||||||
( 1) A ( 1) ( 1)4 3 M |
|
M |
|
|
|
1 |
2 |
3 |
|
14. |
|
|
|
|
|||||||
43 |
43 |
|
4 |
9 |
6 |
|
||||
43 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
7 |
14 |
7 |
|
|
2. Метод приведения определителя к треугольному виду. Определителем треугольного вида называется определитель, все элементы которого, лежащие по одну сторону от главной диагонали, равны нулю. Значение определителя, в таком случае, равно произведению элементов его главной диагонали.
|
1 |
2 |
3 |
4 |
|
|
|
|
|||||
Пример. Вычислить определитель |
1 |
3 |
4 |
4 |
|
. |
|
1 |
1 |
7 |
4 |
|
|
|
1 |
2 |
5 |
9 |
|
|
Решение. Применяя свойство 8, обнулим сначала элементы первого столбца (за исключением a11 ), потом второго столбца (за исключением a22 ) и
т.д.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
1 |
3 |
4 |
4 |
|
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
7 |
0 |
1 |
1 |
0 |
7 |
0 |
1 |
1 |
0 |
|
|
|
1 |
1 |
7 |
4 |
|
0 |
3 |
4 |
0 |
|
0 |
0 |
7 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
|
|
|
1 |
2 |
5 |
9 |
|
0 |
4 |
2 |
5 |
|
0 |
0 |
6 |
5 |
|
0 |
0 |
6 |
5 |
|
0 |
0 |
0 |
5 |
|
тогда значение определителя равно
7 a11 a22 a33 a44 7 1 1 1 5 35 .
3. ОБРАТНАЯ МАТРИЦА
Квадратная матрица А называется невырожденной, если значение её определителя не равно нулю, в противоположном случае матрица называется вырожденной.
Матрица А 1 называется обратной к |
квадратной матрице |
А, если |
А 1 А АА 1 Е, где Е– единичная матрица. |
Для невырожденной |
матрицы |
А аij , где i, j 1,2,..., n , существует единственная обратная матрица |
|
|
|
|
|
|
|
|
A |
A |
... |
A |
T |
|
|
|
|
|
|
|
11 |
12 |
|
1n |
|
|
А |
1 |
|
1 |
|
|
A21 |
A22 |
... |
A2n |
, |
|
|
|
|
|
|
|
... |
... |
|
|||
|
det |
A |
|
|
|||||||
|
|
|
... ... |
|
|
||||||
|
|
|
|
|
|
A |
A |
... |
A |
|
|
|
|
|
|
|
|
n1 |
n 2 |
|
nn |
|
|
где Aij - есть алгебраические дополнения элементов aij |
матрицы |
||||||||||
рица A - вырождена ( det A 0 ), то обратной к ней не существует. Пример 1. Найти матрицу А 1 , обратную к матрице
|
1 |
1 |
0 |
|
|
2 |
3 |
4 |
|
A |
. |
|||
|
1 |
2 |
2 |
|
|
|
Решение. Вычисляем det A 10 0 , значит A - не вырождена и ет. Найдем алгебраические дополнения элементов матрицы A :
A . Если мат-
А 1 существу-
A ( 1)1 1 |
|
3 4 |
|
|
2 ; |
A ( 1)1 2 |
|
2 |
4 |
|
8 ; A ( 1)1 3 |
|
2 |
3 |
|
7 и т. д. |
|||||||||
|
|
|
|
|
|
||||||||||||||||||||
11 |
|
2 |
2 |
|
|
|
|
12 |
|
|
1 |
2 |
|
|
13 |
|
|
|
1 |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A21 2; A22 2 ; A23 3; A31 4 ; A32 4 ; A33 1. |
|
|
|
|
|
|
|
||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
Т |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
8 |
|
7 |
|
|
|
0,2 |
0,2 |
0,4 |
|
||||||
|
|
|
A |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
3 |
|
|
0,8 |
0,2 |
0,4 |
. |
|||||||
|
|
|
|
|
|
10 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
4 |
1 |
|
|
|
|
0,7 |
0,3 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|||||||||||
Пример 2. Найти матрицу X из матричного уравнения XA B , где
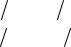
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
3 |
7 |
|
B |
|
0 |
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
, |
|
|
|
|
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
Решение. Из матричного уравнения XA B найдем X , для этого умножим обе |
|||||||||||||||||||||||||
части уравнения слева на А 1 : |
XAA 1 BA 1 , |
тогда X BA 1 , где обратная к A |
|||||||||||||||||||||||
|
|
|
|
A 1 |
|
1 |
|
|
2 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
матрица имеет вид |
|
|
|
|
|
. Поэтому |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
13 |
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
X BA |
1 |
0 |
2 |
|
1 |
|
|
2 |
7 |
|
|
|
1 |
|
|
2 |
6 |
2 13 |
6 13 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
13 |
|
1 |
|
|
|
|
|
|
|
3 |
4 |
|
|
|
|||||||
|
|
1 |
1 |
|
3 |
|
|
13 |
|
3 13 |
4 13 |
||||||||||||||
|
|
|
|
4. |
|
РАНГ МАТРИЦЫ. БАЗИСНЫЙ МИНОР |
|||||||||||||||||||
Выделим в произвольной прямоугольной матрице |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
a ... |
a |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
12 |
|
|
|
1m |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 ... |
a2m |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
А = |
|
... ... |
... |
, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
an 2 ... |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
an1 |
anm |
|
|
|
|
|||||||||
k произвольных столбцов и k произвольных строк, где k min n, m . Определи-
тель k-ого порядка, составленный из элементов матрицы A , расположенных на пересечении выделенных строк и столбцов, называется минором k-ого порядка матрицы A .
Рангом матрицы A называется наибольший порядок минора отличного от нуля, их может быть несколько.
Базисным минором является всякий отличный от нуля ее минор, порядок которого равен рангу данной матрицы.
Основные методы вычисления ранга матрицы
Метод приведения к трапециевидной форме заключается в том, что с по-
мощью элементарных преобразований, которые не изменяют ранга матрицы, она приводится к виду
b |
b |
b |
... |
b |
... |
b |
|
|
|
|
11 |
12 |
13 |
|
1r |
|
1n |
|
|
|
0 |
b22 |
b23 |
... |
b2r |
... |
b2n |
|
|
... ... |
... ... ... |
... ... |
|
|
|||||
|
0 |
0 |
0 |
... |
b |
... |
b |
|
, |
В |
|
||||||||
|
0 |
0 |
0 |
... |
rr |
... |
rn |
|
|
|
0 |
0 |
|
|
|||||
|
0 |
0 |
0 |
... |
0 |
... |
0 |
|
|
|
|
|
|||||||
|
0 |
0 |
0 |
... |
0 |
... |
0 |
|
|
