Тригонометрия. учебное пособие для иностранных граждан слушателей подготовительного отделения. Некрасова Н.Н., Горяйнов В.В

ВВЕДЕНИЕ

Тригонометрия родом из астрономии и геометрии более чем двухтысячелетней давности. Эта область знания выросла из практики, в процессе решения конкретных задач в астрономии, мореплавании и составлении географических карт. Она получила развитие, начиная с Клавдия Птолемея, составившего первые таблицы синусов, основывающиеся на его теореме о соотношении диагоналей и сторон четырехугольника, вписанного в окружность.

Тригонометрический материал широко востребован в вузовском курсе математики: изучение колебаний маятника, электрического тока, волновой теории света не возможны без знания тригонометрических функций.

Настоящее пособие предназначено для студентов-иностранцев, обучающихся на подготовительном факультете. Цель пособия – ознокомить учащихся с русской математической лексикой, сформулировать фундаментальные умения и навыки, необходимые при дальнейшем изучении курса математики и смежных предметов.

В учебном пособии приведены таблицы, графики функций, методические указания к решениям, значительное количество подробно решенных задач (как типовых, так и повышенной сложности), а также упражнения, адресованные учащимся для самостоятельного решения.

Основные понятия и факты соответствующего материала изложены в доступной языковой форме, его последовательность определяется спецефическими особенностями повторительного курса в условиях различного уровня первоночальной математической подготовки иностранных учащихся. В целом, пособие ориентировано на адаптационный этап преподавания математики на русском языке как иностранном.

Авторы выражают благодарность кандидату физ.-мат. наук, доценту А.Б. Кущеву, внимательно прочитавшему рукопись. Его ценные замечания и рекомендации помогли улучшить содержание пособия.

5

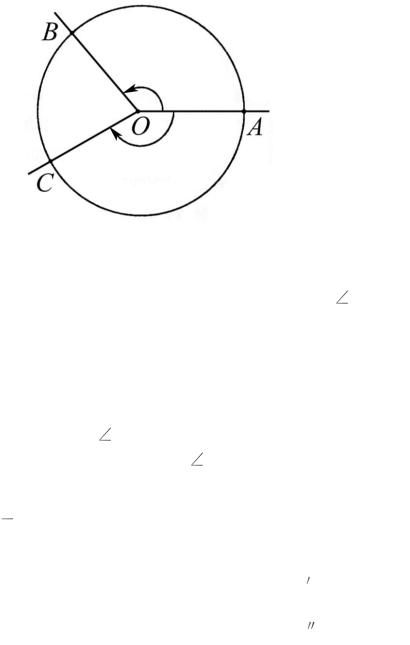
1. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПЛОСКОГО УГЛА

1.1. Градусное измерение углов

Пусть луч, выходящий из точки O, занимает исходное положение OA. Сделав определенный поворот из этого исходного положения против часовой стрелки, он займет положение OB (рис. 1).

Рис. 1. Плоский угол AOB

Лучи OA и OB образуют плоский угол AOB (обозначается AOB ).

Фигура, состоящая из двух различных лучей с общей начальной точкой и ограниченная ими часть плоскости, называется плоским углом.

Угол называется положительным, если он образован поворотом луча

Если стороны угла образуют прямую, то такой угол называется развернутым. Значение развернутого угла равно1800.

6

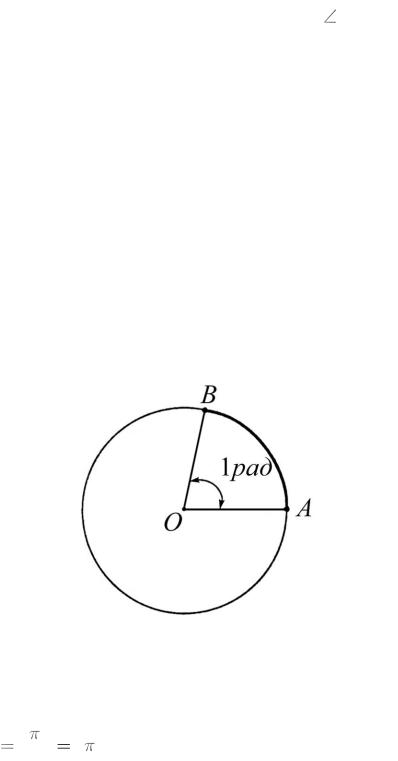
Если луч сделает полный оборот (т.е. займет прежнее место), то описанный им угол называется полным. Значение полного угла равно 3600.

При вращении луча от начального положения OA до любого конечного положения (рис. 1), он может совершить несколько полных положительных или отрицательных поворотов. Т.е. углы по абсолютной величине могут быть сколько угодно большими, и для того, чтобы задать угол AOB , недостаточно знать его начальную и конечную стороны, а нужно указать еще тот поворот, который переводит луч из положения OA в положение OB .

Таким образом, плоский угол может принимать любые положительные и отрицательные значения.

Два угла называются равными, если их значения равны.

1.2. Радианное измерение углов

Угол, равный 1 радиану - это угол, опирающийся на дугу окружности,

длина которой равна радиусу этой окружности.

Радианная мера любого угла AOB есть отношение длины дуги OA , описанной произвольным радиусом из центра O и заключенной между сторонами угла, к радиусу OA этой дуги (рис. 2).

Рис. 2. Радианное измерение угла

Если радиус этой окружности совершит полный оборот, то получится

7

Использование радианной меры углов позволяет придать многим формулам более простой вид.

Полезно запомнить наиболее часто встречающиеся углы, которые представлены в табл. 1.

2. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ОСТРОГО УГЛА

2.1. Определения функций

Рассмотрим единичную окружность, т. е. окружность с центром в начале координат и радиусом равным единице. Осями координат плоскость и

9

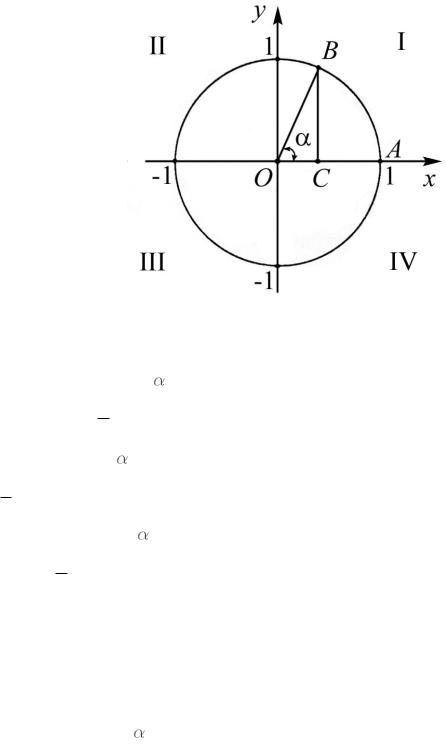
Рис. 3. Единичная окружность с центром в начале координат

Котангенсом угла называется отношение абсциссы точки B к ее ординате: ctg xy .

Секансом угла называется отношение единицы к абсциссе точки B :

sec 1x .

Косекансом угла называется отношение единицы к ординате точки

B : cosec 1y .

Подставляя значения x и y , получим

следовательно, единственное значение любой тригонометрической функции этого угла.

Так как радиус окружности равен 1, то значение синуса числового аргумента читаем на оси ординат единичной окружности, а значения косинуса числового аргумента – на оси абсцисс единичной окружности.

10