Методическое пособие 668

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Пример. Найти

s i n , t g ,еслиc t известноg

Пример. Найти

s i n , t g ,еслиc t известноg

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

3.68 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

	ctgx ctg(x k),		k Z,
для всех	x из области определения функции;

5)	нули функции: ctgx 0 при x 2 k,			k Z;
6) промежутки знакопостоянства:
	ctgx 0 при x ( k;			k),
	ctgx 0 при x ( k;		2	k),
	k Z, ctgx 0 при x ( k;				k),		k Z;
		2
7) монотонность: функция убывает в интервалах
	k;	k ,	k ;
8)	функция непрерывна и	имеет производную					при любом значении
аргумента из области определения функции:			(ctgx)				1	.

						sin2 x
						sin2 x

4. ОСНОВНЫЕ СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ

4.1. Соотношения между тригонометрическими функциями одного и того же угла

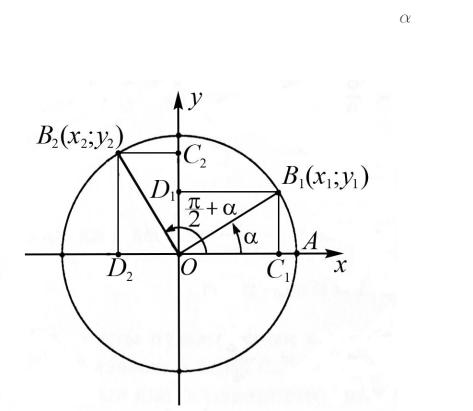
Пусть при повороте радиуса OA единичной окружности вокруг точки

O на угол	получен радиус	OB (рис.12).
На единичной окружности x			cos	, y	sin , где x	абсцисса точки
B , а y	её ордината. Так как точка B			принадлежит единичной окружности
с центром в начале координат,		то ее координаты удовлетворяют уравнению
		x2	y2	R2.		(6)
Подставляя значения x,		y,	R , получим
		sin2 x	cos2 x		1.	(7)

Равенство (7) называют основным тригонометрическим тождеством,

оно справедливо при любых значениях угла .

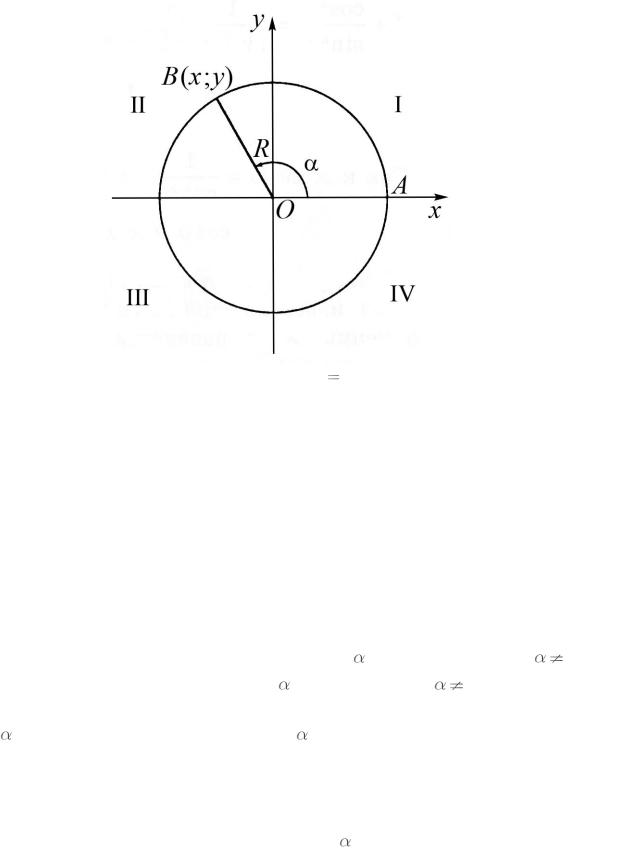
Рис. 12. Окружность с радиусом R

1 и центром O(0; 0)

Как мы уже знаем, tg =

ctg =

подставляя

значения

и y

получим

sin

;

(8)

cos

ctg

cos

;

(9)

sin

tg ctg 1.

(10)

Равенство (8) верно при всех значениях

, при которых c o s

0 а,

равенство (9) верно при всех значениях

, при которых sin

Равенство (10) показывает, как связаны между собой тангенс и котангенс

угла . Оно верно при всех значениях

, при которых

tg и ctg

имеют

смысл.

Выведем формулы, выражающие соотношения между тангенсом и косинусом, а также между котангенсом и синусом одного и того же угла.

Разделим обе части равенства (7) на cos2					получим
	sin2	1
		1		,	т. е.
	cos2	1	cos2	,	т. е.
		22

1 tg2

(11)

cos2

Разделив обе части равенства (7)

на sin2

получим

cos2

, т. е.

sin2

1 ctg2

(12)

sin2

Так как sec

cosec

, то

cos

sin

cos sec 1 и

cosec sin 1.

Если известна одна из тригонометрических функций то, используя полученные выше равенства, можно вычислить все остальные тригонометрические функции угла (с учетом того, в какой четверти лежит заданный угол).

Пример.			Найти					cos			, tg			, ctg								если				известно,			что
sin	3	,		3		.
sin	5	,	2			.
	5		2
Решение.			Найдем cos . Из равенства (7) выразим
								cos2 1 sin2 ,
т.к. угол		лежит в III четверти, то его косинус отрицателен. Значит,

																				9			4	.
				cos				1 sin2									1			9			4
				cos				1 sin2									1
																				25	5
Зная синус и косинус угла									,		можно найти его тангенс и котангенс:
							sin				3				4			3		ctg					1		4
			tg										:						;									.
			tg				cos				5		:		5			4	;						tg		3	.
							cos				5				5			4							tg		3
Ответ: cos					4		; tg		3	;		ctg				4	.
Ответ: cos							; tg		4	;		ctg					.
			5						4							3

Решение. Из равенства (7) получим

										sin2 1 cos2 .
С учетом того, что угол													лежит в IV											четверти,											а синус в этой четверти
отрицателен, то получим:

																								2
																				1										8								2		2
											2									1										8								2		2
	sin					1 cos										1																									.
	sin					1 cos										1														9								3			.
																					3									9								3
		sin
	tg						2 2						1	2								ctg								1										1		2	.
							2 2				:		1					2;												1										1		2
											:							2;												tg
		cos					3					3																		tg								2		2		4

			2		2																									2		.
Ответ: sin			2		2			; tg 2								2; ctg														2
Ответ: sin								; tg 2								2; ctg
					3																					4
Пример. Найти sin								, cos					, ctg				, если tg 10																				и			.
																																						2
Решение. Из равенства (11) получим
				cos2								1										1								1				.
				cos2																														.
											1 tg2							1		100 101
Угол лежит во						II		четверти, поэтому его косинус отрицателен. Значит,

									cos							1									1			.
									cos																			.
												101											101
Из равенства (8) получим
																										1										10
		sin tg cos ( 10)																																					.


																										101										101
Из равенства (10) получим													ctg					1									1		.
Из равенства (10) получим													ctg					tg								10			.
																		tg								10
Ответ: cos					1				; sin						10				; ctg												1		.
Ответ: cos									; sin										; ctg											10			.
					101							101																		10

называют формулами приведения.

4.2.1. Формулы приведения для синуса и косинусов угла 2

1. Докажем, что для любого α выполняются равенства

					sin .
	sin		cos , cos		sin .
		2		2
	Повернем радиус	OA единичной		окружности на		угол	и на угол
	, при этом, радиус OA займет положения OB1				и OB2	(рис. 13).
2	, при этом, радиус OA займет положения OB1				и OB2	(рис. 13).
2

Рис. 13. Синус и косинус углов 2

Опустим из точки B1 перпендикуляры B1C1 и B1D1 на оси координат. Получим прямоугольник OD1B1C1 . Повернем этот прямоугольник вокруг начала

координат на угол 2 . Тогда точка B1 перейдет в точку B2 , точка C1 перейдет в точку C2 на оси OY , точка D1 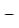в точку D2 на оси OX . Очевидно, что

B1C1 B2C2		и OC1 OC2 . Обозначим координаты точки		B1	через x1 и	y1 ,	а
координаты точки B2 через x2 и y2 . Тогда x1 y2			и	x2 y1.
	Так как окружность единичная, то x1 cos y1		sin ,					,
	Так как окружность единичная, то x1 cos y1		sin ,		x2 cos			,
					2
y2
y2	sin	. Сделав несложные подстановки, получим
	2

		cos ,
sin		cos ,
	2

		sin.
cos		sin.
	2

2. Докажем, что для любого выполняются равенства

		cos ,
sin		cos ,
	2

		sin.
cos		sin.
	2

Представим разность			в виде суммы		( ) , тогда
	2			2


sin		sin
2		2

cos		cos
2		2

( ) cos( ) cos;

( ) sin( ) sin.

4.2.2.Формулы приведения для синуса и косинуса углов

1.Докажем, что для любого выполняются равенства

	sin( ) sin, cos( ) cos .
При повороте радиуса		OA единичной окружности на угол и на угол
точка	A перейдет	соответственно в точки B1 и B2 , которые

симметричны относительно начала координат (рис. 14). Абсциссы и ординаты точек, симметричных относительно начала координат, равны по модулю и противоположны по знаку.

Отсюда следует, что

sin( ) sin и cos( ) cos .

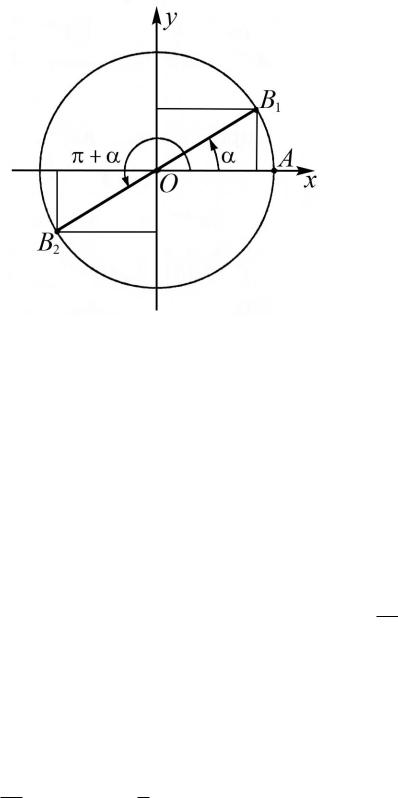
Рис. 14. Синус и косинус углов

2. Докажем, что для любого выполняются тождества

sin( ) sin,	cos( ) cos .
Представим разность в	виде суммы ( ) . Подставим это

значение в полученные выше формулы, получим

sin( )=sin[ +( α)]= sin( α)=sinα; cos( α)=cos[ (α)]= cos( α)= cosα.

4.2.3.Формула приведения для синуса и косинуса углов 32

1.Докажем, что для любого выполняются равенства

	3
sin		cos
sin	2	cos
	2

		3
и	cos		sin .
и	cos		sin .
		2

Представим 32 + в виде π2 (π α) и применим последовательно

полученные выше формулы:

3
sin		+	sin

	2			2

(π ) cos( ) cos ;

2. Представив

в виде

( ) , нетрудно получить, что

3π

sin

cos

и cos

sin .

4.2.4. Формулы приведения для синуса и косинуса углов 2

При изменении угла на целое число оборотов значения синуса и косинуса не изменяются:

sin(2 ) sin и cos(2 ) cos .

Справедливы также формулы:

sin(2 ) sin и cos(2 ) cos ,

так как sin 2 () sin() sin и cos 2 ( ) cos( ) cos .

4.2.5. Формулы приведения для тангенса и котангенса

Эти формулы можно получить с помощью формул приведения для синуса и косинуса:


tg	2

ctg( + )=


	sin	2		cos
					ctg ,
				sin

cos		2

	cos( )		cos		ctg .
	sin( )		sin

Все формулы приведения сведем в табл. 3.

Таблица 3

Формулы приведения

название функции не изменяется

название функции

изменяется

на сходное

(ко-функцию)

sin x

sin

cos

cos x

cos

sin

tgx

ctg

ctgx

ctg

По табл. 3 легко проследить закономерности, имеющие место для формул приведения. Так как все тригонометрические функции имеют период, сформулируем общее правило, по которому можно записать любую формулу приведения не пользуясь табл. 3:

1. перед приведенной функцией ставится тот знак, который имеет приводимая функция в соответствующей четверти, если считать, что угол α

является углом первой четверти;
2. если угол	откладывается от		горизонтальной оси ( k ) , то
название исходной функции сохраняется;			если угол откладывается от
	2k 1
вертикальной оси		- то название исходной функции меняется на
вертикальной оси		- то название исходной функции меняется на
	2

"кофункцию" (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).

3
Пример. Упростим выражение tg		.

	2

3
Решение. Угол		лежит в третьей четверти. Тангенс угла этой
Решение. Угол		лежит в третьей четверти. Тангенс угла этой
2
четверти положителен.	Согласно второму правилу,		название функции
		3
изменяется с тангенса на котангенс. Следовательно, tg			ctg .
изменяется с тангенса на котангенс. Следовательно, tg			ctg .
		2
		29

Пример. Упростим выражение cos( ) .

Решение. Угол ( ) лежит во второй четверти. Косинус угла этой

четверти отрицателен. Согласно второму правилу, название функции сохраняется. Следовательно, cos( ) cos .

4.3. Тригонометрические функции суммы и разности двух углов

4.3.1. Косинус суммы и косинус разности двух углов

Повернем радиус OA единичной окружности вокруг точки O на угол и на угол (рис. 15). Получим радиусы OB и OC .

Рис. 15. Поворот единичного радиуса на углы		и

Найдем скалярное	произведение векторов OB	и OC . Абсцисса	и
ордината точки B равны	x1 и y1 , абсцисса и ордината точки C равны x2		и

y2 .Векторы OB и OC имеют такие же координаты, как и координаты точек B и C .

Вычислим скалярное произведение векторов OB (x1 , y1 ) и

OC (x2 , y2 ) с заданными координатами по формуле

ОB ОС x1 x2 y1 y2 .

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20223.5 Mб4Методическое пособие 663.pdf
#
30.04.20223.5 Mб1Методическое пособие 664.pdf
#
30.04.20223.51 Mб17Методическое пособие 665.pdf
#
30.04.20223.56 Mб10Методическое пособие 666.pdf
#
30.04.20223.65 Mб4Методическое пособие 667.pdf
#
30.04.20223.68 Mб3Методическое пособие 668.pdf
#
30.04.20223.71 Mб3Методическое пособие 669.pdf
#
30.04.2022730.62 Кб22Методическое пособие 67.doc
#
30.04.2022340.58 Кб6Методическое пособие 67.pdf
#
30.04.20223.72 Mб5Методическое пособие 670.pdf
#
30.04.20223.72 Mб8Методическое пособие 671.pdf