Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методическое пособие 668

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

3.68 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

arccos x

arccos(

arcsin x;

arc tgx

arctg(

arcc tgx

arcsin

;

arcctgx

arcctg(

arc tgx

arccos

Для вычисления значений обратных тригонометрических функций при отрицательных значениях аргумента используют следующие тождества:

arcsin(

arcsinx;

arccos(

arccos x;

arc tg(

arctgx;

arcctg(

arcctgx.

arccos

Например: arccos

Для любого числа x 0;1 справедливы тождества:

arcsin x arccos 1 x2 ;

arccos x arcsin

1 x2

(x 0).

Для любого числа x 0; справедливы тождества:

arctgx arcctg

arcsin

arccos

(x 0).

1 x2

Приведем несколько примеров вычисления значений обратных

тригонометрических функций.

Пример. Вычислить значение выражения

2arcsin

arcctg 1 arccos

arccos 1 .

Решение. Пользуясь табличными значениями аргументов тригонометрических функций, получим

																3
		3		arcsin		3				arcctg 1		arcctg1=				3
arcsin									;								;
arcsin		2				2		3	;						4	4	;
		2				2		3							4	4

	1		arccos		2
arccos	1				2		;			arccos	1		arccos1	0 ;
					2	4

		2
										61

Подставим полученные значения в заданное выражение:

					3						1			2	3							5
	2																						.
	2		3		4									3		4						6	.
			3		4			4 2						3		4				4 2		6
Ответ:	5	.
Ответ:		.
6
Пример. Вычислить:
									;									arcsin
			1				3										1				2 2
1) sin			1	arcctg			3						2) sin				1				2 2			;
1) sin				arcctg									2) sin											;
			2													2					3
			2				4									2					3

						3		1				3							arctg2 arctg3.
3) tg			5arctg							arcsin				;		4)
3) tg			5arctg							arcsin				;		4)
					3			4				2

Решение
		3	x , тогда	ctgx	3			x
1) Пусть	arcctg					. Требуется найти	sin		.
1) Пусть	arcctg					. Требуется найти	sin		.
		4			4			2

Известно, что sin														x					1 cos x							, где			x		- угол			в I четверти, тогда													sin	x	0 и
Известно, что sin																										, где					- угол			в I четверти, тогда													sin		0 и
														2									2			2																					2

sin		x			1 cos x							. Найдем										значение cos x по формуле																				c o sx				c t gx				или
sin		2		2								. Найдем										значение cos x по формуле																				c o sx								или
		2		2																																									1 c t g x
																																															2
							3							3
																		3
cos x				4										4				3		(угол x во II четверти).

				1				9			5							5
											5

											4

				16

																										3
																											1
																	1 cos x
			Значит,							sin			x				1 cos x											5				8	4						2		.


											2										2					2					10		5						5

																		2			2									sin x			2			2
			2) Пусть							arcsin														x		, тогда												,
			2) Пусть							arcsin								3						x		, тогда									3			,
																		3																	3

																																								2
		x			1 cos x											1 cos x																			2		2			2				8	1
sin																									, где cos x 1																		1				(cos x 0)
sin		2		2																	2				, где cos x 1											3							1	9	3		(cos x 0)
		2		2																	2															3								9	3

					1				1
	x								1						2						1

sin						3																		.

		2		2											6						3
		2		2											6						3
																										62

3) Так как

tg 5 6


arctg		3			и arcsin			3		, то имеем:
		3		6			2		3

	1					5			3
			tg					tg			tg		tg		1.
	4								4			4		4
		3				6 12

		4) Пусть arctg2+arctg3=x , тогда
		tgx tg(arctg2+arctg3)=										tg(arcctg2)+tg(arctg3)						2 3	1.
		tgx tg(arctg2+arctg3)=										tg(arctg2) tg(arctg3)						2 3	1.
										1		tg(arctg2) tg(arctg3)					1	2 3
Так как arctg2<					и			arctg3<						, то		arctg2+arctg3< ,
		4			2		4						2			2
т.е.		x ,	тогда x			3			.
т.е.		x ,	тогда x						.
	2						4
		Ответ:	1)	2	; 2)		1				; 3)-1;		4)	3	.
														4

			5				3

8. ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ

Простейшими тригонометрическими уравнениями называются уравнения

sin х a,

cos x a,

tg x a,

ctg x a.

8.1.Решение уравнения sin x a

1.Функция y sin x является ограниченной, так как область изменения синуса – промежуток 1;1 , поэтому если a 1, то уравнение решений не

имеет.

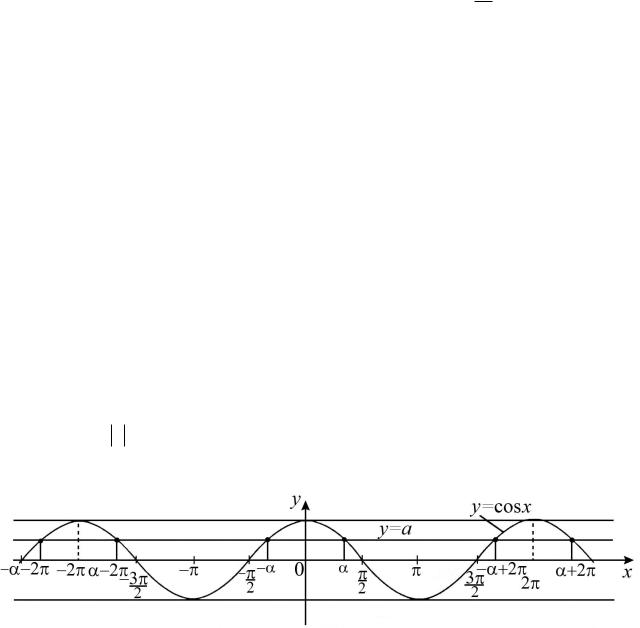
2. Прямая y a пересекает синусоиду бесконечное количество раз (рис.24). Это означает, что при a 1 уравнение sin x a имеет бесконечное количество корней. Так как функция y sin x имеет период 2 , то достаточно найти все решения в пределах этого периода.

Рис. 24. Графики функций y a и y sin x

Из рис. 24 видно, что при	a	1	на отрезке 0;2 есть два числа, синус

которых равен a : это arcsin a		и	arcsin a . Все другие решения
уравнения sin x a получаются		из	двух найденных углов прибавлением
периода.
Итак, пусть arcsin a − будет			решением уравнения sin x a при		a	1.

Тогда все решения этого уравнения определяются по формулам
x arcsin a 2 k,	x arcsin a 2 k,где k Z .
Эти две формулы можно объединить в одну:
x 1 k arcsin a k,k Z .				(48)

3. Рассмотрим частные случаи уравнения sin x a .

a)sin x 1. Прямая y 1 и синусоида имеют бесконечное количество

общих точек (рис. 24). В пределах одного периода x		,	учитывая
периодичность синуса, запишем все решения уравнения sin x 1:	2


x 2 2 k,k Z .			(49)

б) sin x 1. Прямая y 1 и синусоида имеют бесконечное количество общих точек (рис. 24). В пределах одного периода x 2 , с учетом периода синуса, получим все решения уравнения sin x 1:


		x 2 2 k,k Z .									(50)
в) Из рис. 24 видно,	что прямая				y 0			(ось Ох) и синусоида имеют
бесконечные количество общих точек. Решением уравнения будут
0, , 2 , 3 ,..., общая формула которых,						имеет вид:
			x k,k Z.								(51)
Пример. Решим уравнения: а) sin 3x						1	;	б) sin 2x 0;	в) sin	x	1 0.
Пример. Решим уравнения: а) sin 3x							;	б) sin 2x 0;	в) sin		1 0.
						2			2
Решение. а) По формуле (48) получим
3x	1	k		1
			arcsin		k			,k Z.
			arcsin		k			,k Z.
				2
			64

Так как

	1
arcsin			, то
arcsin			, то
	2	6

3x 1	k		k,k Z;
3x 1			k,k Z;
		6

Учитывая, что 1	k		1	k


		18

x 1		k


				18
1			1 k 1
1	18		1 k 1
	18

k ,k Z. 3

18 , получим

x 1 k 1

,k Z;

б) по формуле (51) получим

2x k,k Z;x

,k Z;

в)

преобразуем уравнение к виду

sin

1 и воспользуемся формулой

(49). Получим

2 k,k Z;x 4 k,k Z.

8.2. Решение уравнения cos x a

Функция y cos x является ограниченной. Следовательно, при

уравнение cos x a корней не имеет.

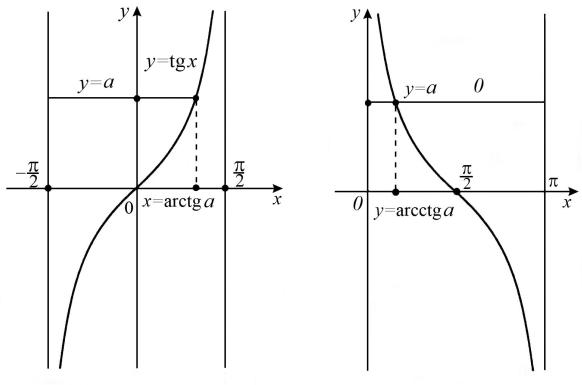
2. При a 1 уравнение имеет бесконечное количество корней. Из рис. 25

видно, что в пределах одного периода уравнение cos х a имеет два корня:

и .

Рис. 25. Графики функций y a и y cos x

Все решения уравнения cos х a записываются двумя формулами:

х 2 k,x 2 k,k Z.

Эти две формулы можно объединить в одну, учитывая, что arccos c : x 2 k arccos a 2 k, k Z.

Таким образом, все решения уравнения cos x a записываются формулой

	x arccos a 2 k, k Z.	(52)
3. Рассмотрим частные случаи уравнения cos х a .
а) cos х 1. Прямая	y 1 и косинусоида имеют бесконечное количество

общих точек (см. рис. 25). В пределах одного периода x 0 и x 2 . С учетом периодичности косинуса запишем все решения уравнения cos х 1:

	х 2 k,k Z;	(53)
б) cos х 1. Прямая	y 1 и косинусоида имеют	бесконечное

количество общих точек (рис. 25). В пределах одного периода x . С учетом периодичности косинуса запишем все решения уравнения cos х 1. Получим

	х 2 k,k Z;	(54)
в) cos х 0. Прямая	y 0 (ось Ох) и косинусоида имеют бесконечное

количество общих точек (рис. 25).

Все решения уравнения cos х 0 с учетом записываются так:


					х 2 2 k,k Z ,
или

					х	2 k,k Z .
Пример. Решить уравнения:
а) cos 2х	1	;	б) cos	х	1;	в) cos8х 1;
а) cos 2х	2	;	б) cos	5	1;	в) cos8х 1;
	2			5

периодичности косинуса

(55)

(56)

	4х		0.
г) cos	4х		0.
		4

Решение.

а) Корни уравнения cos 2х 12 получим, используя формулу (52):

Вычислив
Вычислив	arccos

				1
	2х arccos				2 k,k
	2х arccos				2 k,k
				2
1		arccos	1				2


2			2			3	3

получим

2х

2 k , откуда

k,k Z;

б) используя формулу (53), запишем

2 k , откуда х 10 k,k Z;

в)

используя

формулу

(54),

запишем

8х 2 k,

откуда

k ,k Z;

k , откуда x

г) по формуле (56) запишем

8.3. Решение уравнений tgx a и ctgx a

Область изменения

тангенса и

котангенса

– все

множество R

действительных чисел. Поэтому уравнения tgx a и ctgx a имеют решения при любом a.


В пределах одного периода (у функций tgx a и				ctgx a он равен )
прямая	y a	пересекает тангенсоиду только один раз,		т.е. уравнение tgx a
имеет	одно	решение в пределах одного	периода. Это – угол x arctg a
(рис. 26, а). Для уравнения ctgx a это угол			x arcctg a (рис. 26, б).

а)		б)
Рис. 26.	Графики функций y a ,	y tg x и y ctg x
	67

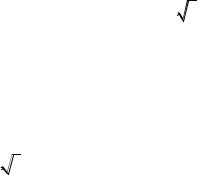
Все остальные решения получаются прибавлением периода, т.е.:

x arctg k, k Z;		(57)
x arcctg k, k Z.		(58)

Пример. Решить уравнения: tgx 1;	ctgx	3	.

		3

Решение. Используя формулы (57) и (58), получим

x arctg ( 1) k arctg1 k k,k Z. 4

x arcctg	3	k		k,k Z.
	3		3

9.СПОСОБЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Впредыдущем разделе приведены формулы корней простейших тригонометрических уравнений sin x a , cos x a , tgx a и ctgx a . К этим

уравнениям сводятся также другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение формул преобразования тригонометрических функций.

9.1. Простейшие тригонометрические уравнения

Пример. Решить уравнения:

1) cos 2x 0;

2) cos3x 1;

3) cos

;

4) cos

1,5 .

Решение.

cos2x 0,

n Z ;

cos3x 1,

3x 2 n ,

2 n

n Z ;

cos

;

arccos

2 n, n Z

или

2 n ,

откуда

4 n,

n Z ;

cos

1,5 - уравнение не имеет

корней, так как

cos

Ответ:					1)		x			n , n Z ;					2) x			2 n	, n Z ;
Ответ:					1)		x			n , n Z ;					2) x				, n Z ;
									4		2				3			3
					3) x					2	4 n, n Z ;				4) корней нет.
					3) x					3	4 n, n Z ;				4) корней нет.
										3
Пример.				Решить уравнения:
								x	1		2) 2sin x				3) sin x(2sin x 1) 0 .
	1)				sin			x		;				3 ;
	1)				sin					;				3 ;
							2
Решение.
1)	sin	x	1	,		x			2 n ,				x 4 n,		n Z ;
1)	sin		1	,					2 n ,				x 4 n,		n Z ;
	2				2				2

	2sin x							sin x			3	,	x ( 1)n arcsin			3	n, n Z или
2)					3 ,						3					3
2)					3 ,
											2				2
													x ( 1)n n, n Z .
														3
3) sin x(2sin x 1) 0 ,											откуда sin x 0				или 2sin x 1 0 , т.е.						sin x	1	.
3) sin x(2sin x 1) 0 ,											откуда sin x 0				или 2sin x 1 0 , т.е.						sin x	2	.
																						2
Из уравнения sin x 0									имеем x n, n Z .						Из уравнения sin x					1	получим
Из уравнения sin x 0									имеем x n, n Z .						Из уравнения sin x						получим
																		2
x ( 1)n n, n Z .
	6
Ответ: 1)					x 4 n, n Z ;									2)	x ( 1)n			n, n Z ;
															3

3) x n, x ( 1)n 6 n, n Z .

				Пример. Решить уравнения:
										1)		tg3x = 0 ;					2)		tg		x		1;			3)
										1)		tg3x = 0 ;					2)		tg				1;			3)
																				2
				Решение.
1)		tg3x=0,						3x= n ,					x		n	,	n Z ;
1)		tg3x=0,						3x= n ,					x		3	,	n Z ;
															3
2)			tg		x	1,			x	n ,					x			2 n, n Z ;
2)			tg			1,				n ,					x			2 n, n Z ;
				2				2		4							2
						x												x							1
3)			ctg			x				3		,	откуда				tg	x							1


						2		4											2			4				3
	x						n ,				x			5	n ,			откуда						x			5
							n ,			2			12		n ,			откуда						x
2			4			6				2			12													6
				Ответ: 1) x								n , n Z ;					2)		x					2 n,
												3											2

x
x			3 .
ctg
ctg
	2	4

иx n , 2 4 6

2 n, n Z .

n Z ; 3) x 56 2 n, n Z .

9.2. Решение уравнений, сводящихся к квадратным
Пример. Решить уравнение sin2 x sinx 2 0.
Решение. Это	уравнение является квадратным	относительно	sin x .
Обозначив sin x t,	1 t 1 получим уравнение t2 t 2 0 . Его		корни
t1 1,t2 2 . Таким	образом, решение исходного уравнения сводится к
решению простейших уравнений:
	sinx 1, sinx 2.

Уравнение sinx 1 имеет корни x 2 2 k,k Z;		уравнение sin x 2

не имеет корней.

Ответ: x 2 k,k Z. 2

Пример. Решим уравнение 3cos2 x sin x 1 0.

Решение. Приведем данное уравнение к одной тригонометрической

функции: sin x .

Используя основное тригонометрическое тождество,

согласно

которому cos2 x 1 sin2 x, получим

3(1 sin2 x) sin x 1 0,

3sin2 x sin x 2 0.

Обозначив

sin x

получим,

3t2 t 2 0,

откуда

Решение исходного уравнения сводится к решению простейших уравнений

sin x 1

sin x

Уравнение sin x 1 имеет корни x

2 k,k Z;

Уравнение sin x

имеет корни

(

1)k arcsin

Ответ: x 2 k, x ( 1)k arcsin

Пример. Решим уравнение 2sin2 x 3cos x 0.

Решение.

Используя тождество

sin2 x 1 cos2 x,

получим:

2(1 cos2

x) 3cos x 0,

2cos2 x 3cos x 2 0.

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20223.5 Mб4Методическое пособие 663.pdf
#
30.04.20223.5 Mб2Методическое пособие 664.pdf
#
30.04.20223.51 Mб17Методическое пособие 665.pdf
#
30.04.20223.56 Mб10Методическое пособие 666.pdf
#
30.04.20223.65 Mб4Методическое пособие 667.pdf
#
30.04.20223.68 Mб3Методическое пособие 668.pdf
#
30.04.20223.71 Mб3Методическое пособие 669.pdf
#
30.04.2022730.62 Кб22Методическое пособие 67.doc
#
30.04.2022340.58 Кб6Методическое пособие 67.pdf
#
30.04.20223.72 Mб5Методическое пособие 670.pdf
#
30.04.20223.72 Mб8Методическое пособие 671.pdf