
Методическое пособие 668
.pdf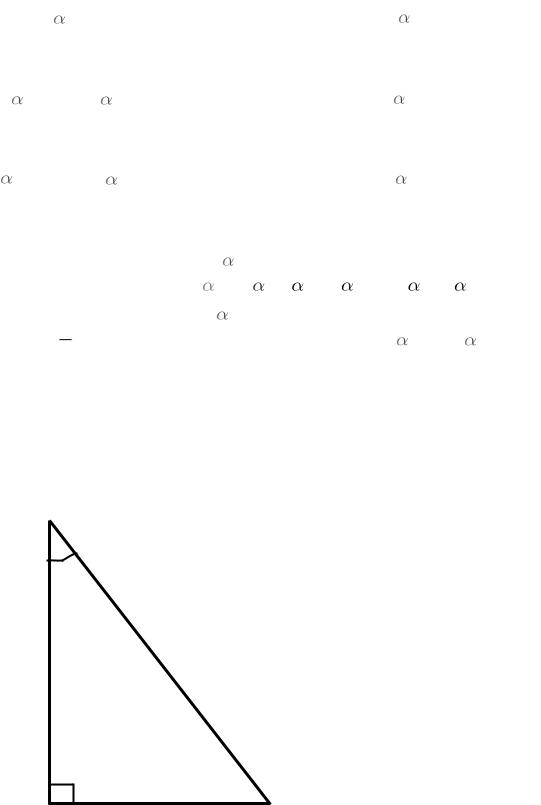
Функции sin и cos определены при любом значении угла , так как для любого угла поворота радиуса единичной окружности можно найти соответствующие значения x и y .
Функции |
tg |
|
и |
sec |
имеют |
смысл |
при |
любом |
, |
кроме |
||||||||
90 ,270 ,450 ,... так как для этих углов дроби |
|
y |
и |
1 |
|
не имеют смысла. |
||||||||||||
|
x |
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Функции |
ctg |
и |
|
cosec |
имеют |
смысл |
при |
любом |
, |
кроме |
||||||||
0 ,180 ,360 ,... для которых не имеют смысла дроби |
x |
и |
1 |
. |
|
|
||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
y |
|
|
||
Каждому |
допустимому значению |
угла |
соответствует единственное |
|||||||||||||||
значение тригонометрических функций |
(sin |
, cos |
, tg , |
ctg , cosec |
sec ). |
|||||||||||||
Как видно из рис. 3, функции |
s i n |
и cos |
|
могут принимать значения, |
||||||||||||||
принадлежащие отрезку |
[ |
1;1], |
а областью значений функций |
tg |
и ctg |
|||||||||||||
является множество всех действительных чисел.
2.2. Соотношение сторон и углов в прямоугольном треугольнике
Из определения тригонометрических функций были выведены формулы соотношения сторон и углов в прямоугольном треугольнике рис. 4.
А
b
катет
С
Рис. 4.
c
гипотенуза
катет |
|
a |
В |
Прямоугольный треугольник
Косинус острого угла прямоугольного треугольника равен отношению
прилежащего катета к гипотенузе |
cos = |
b |
. |
|
|||
|
|
c |
|
|
11 |
|
|

Синус острого угла прямоугольного треугольника равен |
отношению |
||||||||
противолежащего катета к гипотенузе sin = |
a |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
c |
|
|
|
|
|
|
|
Тангенс острого угла прямоугольного треугольника равен |
отношению |
||||||||
противолежащего катета к прилежащему катету |
tg = |
a |
. |
|
|
||||
|
|
||||||||
|
|
|
|
|
b |
|
|||
Котангенс острого угла прямоугольного треугольника равен |
отношению |
||||||||
прилежащего катета к противолежащему катету ctg = |
b |
. |
|
||||||
|
|
||||||||
|
|
|
|
|
|
|
a |
|
|
Выражая из этих формул a, b, c получим, |
|
|
|
|
|
|
|||
a c sin; |
b c cos ; |
a b tg . |
|
||||||
2.3.Значения тригонометрических функций
Втабл. 2 приведены точные значения тригонометрических функций острых углов. Прочерк сделан в тех случаях, когда функция не имеет смысла.
Таблица 2
Значения тригонометрических функций для некоторых углов
|
0 |
|
|
|
30 |
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
60 |
|
|
|
|
90 |
180 |
270 |
360 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
6 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
3 2 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
sin |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
1 |
0 |
1 |
0 |
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
cos |
1 |
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
-1 |
0 |
1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
0 |
1 |
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
0 |
- |
0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctg |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
0 |
- |
0 |
- |
|||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения значений тригонометрических функций углов, кратных 90 , например 180 , 270 , 450  и т.д., можно использовать единичную окружность.
и т.д., можно использовать единичную окружность.
12
Пример. Найти значения тригонометрических функций для углов 180 и
270 .
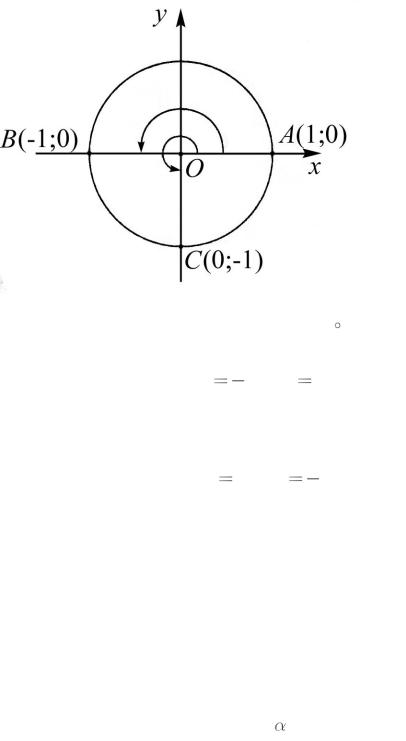
Решение. При повороте на 180 вокруг точки O единичный радиус OA переходит в радиус OB , а при повороте радиуса OA на 270 - в радиус OC (рис. 5).
Рис. 5. Определение углов кратных 90 |
|
|
|
|
|
|
|||||||||
Так как точка B имеет координаты |
x |
1 и y |
0 , то |
|
|
|
|||||||||
sin180 0, |
cos180 1, |
tg180 = |
y |
|
|
0 |
|
0. |
|||||||
x |
1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
Так как точка C имеет координаты |
x |
0 и y |
|
1, то |
|
|
|
||||||||
sin 270 1, |
cos 270 0, |
|
ctg270 = |
x |
|
|
0 |
|
|
0. |
|||||
|
|
|
1 |
||||||||||||
|
|
|
|
|
y |
|
|
|
|||||||
Отметим, что функции ctg180 и tg270 не имеют смысла.
2.4. Знаки тригонометрических функций
Знаки тригонометрических функций угла |
в каждой из четвертей |
приведены на рис. 6. |
|
13 |
|

Знаки синуса и |
Знаки косинуса |
Знаки тангенса |
и косеканса |
и секанса |
и котангенса |
Рис. 6. Знаки тригонометрических функций в координатных четвертях
2.5. Четность и нечетность тригонометрических функций
Функции sin , tg , ctg , cosec |
– нечетные, а функции cos , sec |
– |
|
четные. |
|
|
|
Таким образом, справедливы следующие формулы: |
|
||
sin( ) sin ; |
tg( ) tg; |
|
|
ctg( ) ctg; |
cosec( ) cosec; |
(4) |
|
cos( ) cos; |
|
sec( ) sec . |
|
Например, cos( 400 ) cos40 ; |
|
tg( 60 ) tg60 . |
|
2.6. Периодичность тригонометрических функций
Равномерное движение точки P по единичной окружности,
изображенной на рис. 7 – процесс периодический.
14

Рис. 7. Периодичность движения точки P
Координаты x и y точки P при равномерном вращении будут меняться
(на единичной окружности x |
|
cos , |
y |
sin |
). |
|
|
|
||
Поскольку тригонометрические функции определены с помощью |
||||||||||
координат вращающейся точки, то все они являются периодическими. |
|
|||||||||
Наименьший положительный период (его называют основным периодом) |
||||||||||
функций sin , |
cos , |
sec , |
cos ec |
равен |
T 2 . |
|
|
|
||
Наименьший положительный период функций tg |
и ctg |
равен T |
. |
|||||||
Поэтому |
для всех |
из |
области |
определения |
функции |
справедливы |
||||
формулы: |
|
|
|
|
|
|
|
|
|
|
|
sin sin( 2 k); |
cos cos( 2 k); |
|
|
||||||
|
sec sec( 2 k); |
cosec cosec( +2 k); |
|
(5) |
||||||
tg tg( k); |
ctg ctg( k), k 1,2, |
|
|
|||||||
В приведенных |
выше |
формулах, |
k |
0 если точка двигается против |
||||||
часовой стрелки и k |
0 если точка двигается по часовой стрелке. |
|
||||||||
Например, sin30° sin(30°+360°) sin(30° 360°) =sin(30° 2 360°) sin(30° 2 360°) …
tg45° tg(45°+180°) tg(45° 180°) tg(45° 2 180°) tg(45° 2 180°) …
15

Пример. Найти sin 7650 и cos( 1170)0 .
Решение. Используя формулы (5), получим
sin 7650 sin(2 3600 450 ) sin 450 |
2 |
; |
|
2 |
|||
|
|
cos( 1170)0 cos( 3 3600 900 ) cos( 900 ) cos900 0.
3. ОСНОВНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ И ИХ ГРАФИКИ
3.1. Свойства функции y sin x и ее график
На рис. 8 изображен график функции y sin x, который называют
синусоидой.
Рис. 8. График функции y sin x
Отметим основные свойства функции y sin x :
1)область определения 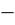 множество R всех действительных чисел;
множество R всех действительных чисел;
2)область изменения (множество значений) - отрезок 1;1 , значит
y sin x - функция ограниченная;
3) |
функция - нечетная, т.е. sin(x) sin x для всех |
x R; |
|||
4) |
функция - периодическая, с наименьшим периодом T 2 : |
||||
|
sin x sin(x 2 k), |
x R, k Z; |
|
||
5) |
нули функции: sin x 0 при |
x k, |
k Z; |
|
|
16

|
6) |
промежутки знакопостоянства: sin x 0 при |
x (2 k; 2 k), |
||
k Z, |
sin x 0 при |
x ( 2 k; 2 2 k), |
k Z; |
|
|
|
7) |
монотонность: |
|
|
|
|
функция возрастает от 1 до 1 на отрезках |
|
|||
|
|
|
2 k; |
|
|
|
, |
k , |
||
|
|
|
|
|
|
2 k |
||||
|
|
|
2 |
|
2 |
|
|
|
|
|
функция убывает от 1 до 1 на отрезках |
|
|
|
|||||||
|
|
|
|
3 |
|
|
|
|
||
|
|
|
2 k; |
|
|
2 k |
, |
k ; |
||
|
|
|
|
|||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
8) наибольшее значение функции: sin x 1 в точках |
x |
|
2 k, |
k Z , |
|
|
2 |
||||
наименьшее значение функции sin x 1 в точках |
x |
|
2 k, |
k Z; |
|
2 |
|||||
9) функция непрерывна и имеет производную при любом значении аргумента: (sin x) cos x.
3.2. Свойства функции y cos x и ее график
График функции y cos x называют косинусоидой. Он показан на рис. 9.
Рис. 9. График функции y cos x
Свойства функции y cos x :
1)область определения - множество R всех действительных чисел;
2)область изменения (множество значений) - отрезок 1;1 , значит
17

y cos x - функция ограниченная; |
|
|
|
|
|
|
|
|
||||||
|
3) |
функция - четная, т.е. cos(x) cos x для всех |
x R; |
|
|
|||||||||
|
4) |
функция - периодическая, с наименьшим периодом T |
2 : |
|
||||||||||
|
|
|
|
|
|
cos x cos(x 2 k), |
x R, k Z; |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) |
|
нули функции: cos x 0 при |
x |
2 k, |
k Z; |
|
|
|
|||||
|
6) |
промежутки знакопостоянства: |
cos x 0 для всех |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
x |
|
|
|
2 k; |
|
2 k , k Z, cos x 0 |
при x |
|
2 k; |
|
2 k |
, k Z; |
||
|
|
|
|
|
||||||||||
|
|
2 |
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
7) монотонность: |
|
|
|
|
|
|
функция возрастает от |
1 до 1 на отрезках |
|
|
|||
2 k; |
2 k , |
k , |
|
|
||
функция убывает от 1 до 1 на отрезках |
|
|
|
|||
2 k; |
2 k , |
k ; |
|
|
||
8) наибольшее значение функции: cos x 1 в точках x 2 k, |
k Z, |
|||||
наименьшее значение функции cos x 1 в точках x 2 k, |
k Z; |
|||||
9) функция непрерывна и имеет производную при любом значении |
||||||
аргумента: (cos x) sin x. |
|
|
|
|
|
|
3.3. Свойства функции y tgx и ее график |
|
|
||||
График функции y tgx |
называют тангенсоидой (рис.10). |
|
|
|||
Отметим основные свойства функции y tgx : |
|
|
||||
1) область определения |
множество R всех действительных чисел, |
|||||
|
|
|
|
|
|
|
кроме чисел вида x 2 k, |
k Z; |
|
|
|
|
|
2) множество значений - множество R всех действительных чисел,
значит y tgx - функция неограниченная;
18

|
Рис. 10. График функции |
y tgx |
|
|||||||||
3) |
функция - нечетная, т.е. |
tg(x) tgx |
для всех |
x из области |
||||||||
определения функции; |
|
|
|
|
|
|
|
|
|
|
|
|
4) |
функция - периодическая, с наименьшим периодом T |
: |
||||||||||
|
|
|
tgx tg(x k), |
k Z, |
|
|
||||||
для всех x из области определения функции; |
|
|
|
|||||||||
5) |
нули функции: tgx 0 |
|
при |
x k, |
k Z; |
|
|
|||||
6) |
промежутки знакопостоянства: |
|
|
|
|
|||||||
|
tgx 0 |
при x ( k; |
|
k), k Z, |
|
|||||||
|
2 |
|
||||||||||
|
tgx 0 |
при |
x ( |
|
k; |
k), |
k Z; |
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
7) |
монотонность: функция возрастает в интервалах |
|
||||||||||
|
|
|
|
k; |
|
k |
|
k ; |
|
|||
|
|
2 |
2 |
, |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
19 |
|
|
|
|
||
8) функция непрерывна и имеет |
производную |
при |
любом значении |
||
аргумента из области определения функции: (tgx) |
1 |
|
. |
|
|
|
|
|
|||
|
|
|
|||
|
|
cos2 x |
|
||
3.4. Свойства функции |
y ctgx и ее график |
||||
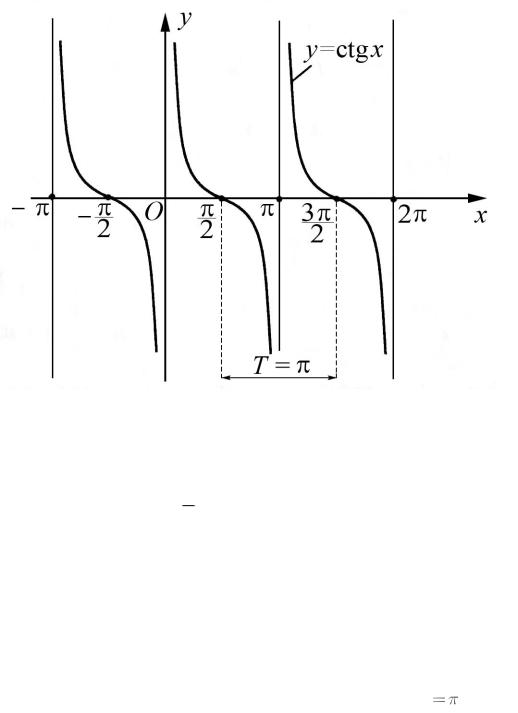
График функции y ctgx называют котангенсоидой, |
она изображена на |
||||
рис. 11. |
|
|
|
|
|
|
Рис. 11. |
График функции |
y ctgx |
|
|
Отметим основные свойства функции y ctgx |
|
||||
1) область |
определения |
множество |
R всех действительных чисел, |
||
кроме чисел вида |
x k, |
k Z; |
|
|
|
2) множество значений - множество |
R всех действительных чисел, |
||||
значит y ctgx - функция неограниченная; |
|
|
|||
3) функция - нечетная, |
т.е. ctg(x) ctgx для всех |
x из области |
|||
определения функции; |
|
|
|
|
|
4) функция - периодическая, с наименьшим периодом T |
: |
||||
|
|
|
20 |
|
|
