Методическое пособие 598

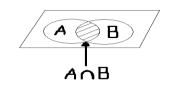
Пусть n A есть количество элементов множества A . Для

определения количества элементов объединения двух множеств применяют формулу:

Она легко объясняется с помощью диаграммы Эйлера-Венна.

Рис. 9. Диаграмма Эйлера-Венна для пересечения двух множеств

Используя формулу (17), можно определить количество элементов объединения любого числа множеств. В частности, для трёх множеств получим:

n A B С n A B C n A n B Cn A B C n A n B n C n B C

n A B A C n A n B n C n B Cn A B n A C n A B A C

n A n B n C n B C n A B n A Cn A B A C n A n B n C n A Bn A C n B C n A B C .

Выведенную формулу также можно пояснить с помощью диаграммы Эйлера – Венна.

61

Рис. 10. Диаграмма Эйлера-Венна для пересечения трёх множеств

Если имеется n слагаемых, то аналогичную формулу можно доказать методом математической индукции.

Теорема 1. Пусть A1, A2 , …, An - некоторые множества

Выражение (18) допускает обобщение. Допустим, что заданы множество Sn из n опеределённых элементов и множество,

включающее k свойств p1, p2 , ..., pk , которые элементы множества Sn могут как иметь, так и не иметь. Возьмём произвольное подмножество свойств pi1 , pi2 , ..., pir . Количество элементов, удовлетворяющих всем r этим свойствам, примем как n pi1 , pi2 , ..., pir . Случай, когда элемент не удовлетворяет

свойству pi , будем записывать как pi .

Вычислим количество элементов, не удовлетворяющих совокупности требуемых свойств. Рассмотрим вначале такие очевидные случаи.

62

1)Допустим, есть одно свойство p , тогда n p n n p .

2)Пусть есть конечное количество свойств p1, p2 , ..., pk ,

n p1, p2 , ..., pk n k n pi .

i 1

3)Предположим, что элементы удовлетворяют наборам

разных свойств. При этом имеет место теорема, подобная теореме 1.

Теорема 2. Предположим, что заданы множество Sn из n определённых элементов и множество, включающее k

1 i j l k

Замечание. Данная теорема 2 справедлива для всякого набора свойств элементов множества Sn , которым они могут как удовлетворять, так и не удовлетворять. Это означает, что

Пример. В комнате находятся несколько человек, владеющих как минимум одним из трёх языков. Шесть владеют английским, шесть – немецким, семь – французским. Четыре владеют английским и немецким, три – немецким и французским, два – французским и английским. Один человек владеет водновременно тремя языками. Какое количество человек находится в комнате? Вычислть, сколько из них владеют только английским языком

Решение. Обозначим через pА свойство владеть английским языком, pН и pФ – свойства, означающие владение

соответственно немецким и французским языками. Поскольку общее количество людей образуют те, кто владеет как минимум одним языком; не владеющих ни одним языком нет. Используя формулу (18), получим:

n n pA n pН n pФ n pA , pН n pA , pФ

n pН , pФ n pA , pН , pФ 6 6 7 4 2 3 1 11.

Количество людей, владеющих только английским языком, есть n pA , pН , pФ . Применим формулу (20):

n pA , pН , pФ n pA n pA , pН n pA , pФ

n pA , pН , pФ 6 4 2 1 1.

Аналогично можно просто найти ответы и на другие вопросы подобного характера.

Учет весов элементов в формуле включений и исключений

Очередные усложнения метода имеют отношение к вводу весов элементов. При этом веса представляют собой числовые характеристики элементов заданных множеств.

64

При этом

Сумму весов для всех имеющихся подмножества из r эле-

членов,

2 pi1 , pi2 p1, p2 p1, p3 ... pk 1, pk

i1 , i2

тов, каждому из которых приписан определённый вес, и множество, включающее k свойств, при этом сумма k 0 весов

элементов, для которых не имеет место ни одно из этих свойств, вычисляется как

Примеры применения метода включений и исключений

Метод включений и исключений используется во всех случаях, когда возникает проблема разбиения дискретных множеств при условии, обладают или нет его элементы заданными свойствами.

67

Пример 1. Задача о беспорядках или задача о встречах

Предположим, что есть конечное упорядоченное множество натуральных чисел 1, 2, ..., n. Они могут образовывать

перестановки a1, a2 , ..., an , количество которых равно n!. В

этой совокупности перестановок есть такие, в которых ни один из элементов не сохранил своего исходного места:

ai i, i 1, n. Подобного вида перестановки называются бес-

порядками. Определим их количество.

Совокупность n элементов исследуется относительно множества свойств pi элементов оставаться на своих местах. Предположим, что k элементов фиксированы, в этом случае количество n k таких перестановок составит n k !. Количество способов, возможных для выделения k фиксированных элементов из всего числа n элементов, составит Сnk . При

этом количество беспорядков, в которых ни один элемент не остался на том иместе, в котором он был вначале, вычисляется подобно выражению (23):

Здесь квадратными скобками обозначена целая часть данного выражения.

Пример 2. Задача о числе перестановок,

в которых остаются на своих местах k элементов

Здесь из n элементов k должны оставаться на своих первоначальных местах. Количество способов, которыми

можно выбрать эти k фиксированных элементов, равно Cnk . Другие n k элементов могут образовывать беспорядки, их количество вычислим по формуле (25). В этом случае, при-

Вопросы для повторения

1.Комбинаторика. Правила суммы и произведения.

2.Перестановки, размещения, сочетания.

3.Перестановки с повторениями. Сочетания с повторения-

ми.

4.Выборка. Выборка с возвращением. Размещение с повторениями. Теорема о числе размещений с повторениями.

5.Бином Ньютона. Биномиальные коэффициенты. Треугольник Паскаля. Свойства биномиальных коэффициентов. Теорема о числе подмножеств конечного множества и следствие из неё. Формула бинома Ньютона для произвольного действительного показателя. Полиномиальная формула. Полиномиальные коэффициенты.

69

6.Подходы для изучения комбинаторных объектов и чисел. Метод рекуррентных соотношений.

7.Производящие функции. Производящая функция для сочетаний с ограниченным числом повторений.

8.Однородные и неоднородные линейные рекуррентные соотношения.

9.Экспоненциальные производящие функции.

10.Метод включений и исключений.

Задачи для самостоятельного решения

1. Какое количество трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5, причём каждая из них может входить в число не более одного раза?

2.Каково количество пятизначных чисел, делящихся на 5?

3.Какое количество двузначных чисел с обеими чётными цифрами?

4.Пассажир поместил багаж в автоматической камере хранения, а когда пришёл получать вещи, оказалось, что забыл номер замка ячейки. На ум ему лишь приходит, что имелись числа 45 и 58. Для получения доступа надо верно ввести комбинацию из пяти цифр. Сколько существует способов перебора номеров, чтобы открыть ячейку камеры?

5.На турнире по гимнастике две команды имели равное число участников. В результате итоговая сумма баллов, набранных всеми спортсменами, оказалась равной 156. Какое количество спортсменов участвовало в турнире, при условии, что любой соревнующийся был оценён 8 или 9 баллами?

6.Имеется царство, в котором любые два жителя различаются составом зубов. Найти максимальное количество жителей царства (наибольшее число зубов у человека равно 32)?

7.В состав роты входят три офицера и сорок солдат. Каково количество способов выделения наряд, состоящего из одного офицера и трёх солдат?

70