Методическое пособие 598

2.3.Линейные рекуррентные соотношения

2.3.1.Метод рекуррентных соотношений

Комбинаторика содержит целый ряд подходов к ис-

следованию объектов и чисел, используемых в ней.

1)Подход, основанный на применении теории мно-

жеств, подразумевает определение количества элементов, содержащихся в конечных совокупностях. Чтобы решить такие вопросы, требуется дополнительная информация, что означает необходимость знания мощностей некоторых подмножеств. Сюда относится, в частности, теорема и формула включений и исключений.

2)Алгебраический подход. Его основу составляет применение вспомогательных, легко выводимых тождеств, используемых в комбинаторике, для определения необходимых пользователю чисел комбинаторики. В качестве примера использования алгебраического подхода можно привести метод рекуррентных соотношений.

3)Использованиение формул обращения. Они опре-

деляют связи, существующие между разными комбинаторными числами, их можно получить по-разному.

4)Метод производящих функций. Применяется для перечисления чисел, используемых в комбинаторике, и определения комбинаторных тождеств.

Вкачестве примера применения алгебраического под-

хода рассмотрим метод рекуррентных соотношений. Его суть заключается в нахождении решения задачи комбинаторики с n объектами находится как решение подобной задачи с

41

меньшим количеством объектов с использованием некоторого соотношения, которое называется рекуррентным (от англ. recurrence – возвращение). Применяя данное соотношение, требуемую величину вычисляют, принимая во внимание, что для малого числа предметов решение задачи, как правило, очевидно, и просто находится.

2.3.2. Метод производящих функций

Производящей функцией последовательности ak на-

зывается частичная сумма (сумма при n ) степенного ряда

n

f a (t) ak t k .

k 0

Подход к применению метода производящих функций состоит в следующем: нужно найти все члены некоторой последовательности ak . Используя рекуррентное соотноше-

42

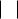
В этом случае производящей функцией последовательности биномиальных коэффициентов является 1 t n , таким обра-

В случае at 1 получим бесконечно убывающую геометри-

Степенные производящие функции, представляемые в

n

виде fa (t) ak t k , соответствуют совокупностям последо-

k 0

вательностей, члены которых представляют собой биноминальные коэффициенты Сnk , а также функции от них.

43

Зададим такие действия для множества степенных про-

изводящих функций fa (t) .

cn an bn a0 b0 , a1 b1,... c0 , c1,... , суммой произ-

k 0

Произведением (по-другому, свёрткой) последователь-

ностей an и bn именуется последовательность

dn anbn d0, d1, ... , здесь

k 0

Числа dk определяются в результате перемножения рядов по формулам (4):

44

Нулём для множества производящих функций fa t

служит производящая функция fa t 0; ей отвечает после-

довательность из нулей 0, 0, 0, ..., 0, ... .

Единицей для множества производящих функций

fa t служит производящая функция fa t 1; ей отвечает единичная последовательность 1, 0, 0, ..., 0, ... e.

Обратным по отношению к операции сложения (по-

другому, противоположный) элемент для множества произ-

k 0

a0 , a1, ..., ak , ... .

Обратным элементом по отношению к операции ум-

ножения для совокупности производящих функций служит

~

функция fa 1 t ak tk , ей отвечает последовательность

k 0

45

an 0, 0, 0, ...,0, ... .

Применяя формулы (4), получим систему:

Искомыми величинами служат в ней a0 , a1, ..., an , их число совпадает с числом уравнений системы.

Умножение производящей функции на число R опреде-

ляется как

k0

2.3.3.Производящая функция для сочетаний

сограниченным числом повторений

Предположим, что элемент xk появляется в сочетаниях из n элементов по m элементов с повторениями 0,1, 2,..., j раз, в этом случае производящая функция имеет вид:

i 1

46

Для того, чтобы вычислить только количество соответ-

Пример. Предположим, что заданы сочетания из объектов 1, 2, 3, при этом не исключена возможность появления 1 и 2 в двух и менее случаях, 3 может встретиться один раз или вообще не появиться. Найдём производящую функцию с по-

мощью выражения (6):

f (t) 1 x1t x12t2 1 x2t x22t2 1 x3t 1 x1 x2 x3 t

x12 x1x2 x1x3 x2 x3 x22 t 2

x12 x2 x12 x3 x1x22 x1x2 x3 x22 x3 t3

x12 x22 x12 x2 x3 x1x22 x3 t 4 x12 x22 x3t5 .

Коэффициент a1 3 здесь есть число сочетаний из трёх эле-

ментов по одному с двумя и менее повторениями; a2 5 – из трёх элементов по два с двумя и менее повторениями; a3 5 –

- из трёх элементов по три при условии появления первого и второго элементов в двух и менее случаях, при этом третий элемент может встретиться один раз или вообще не появить-

47

ся. Если не полагать x1 x2 x3 1, , тогда, в частности, ко-

эффициент при t3 , то есть x12 x2 x12 x3 x1x22 x1x2 x3 x22 x3 , даёт такой набор сочетаний с возможными повторениями: 112, 113, 122, 123, 223. Подобным образом, коэффициент при t 4 представляет собой число сочетаний из трёх элементов по четыре с повторениями, если такое возможно: 1122, 1123, 1223; коэффициент при t5 – число сочетаний из трёх элементов по пять с возможными повторениями: a5 x12 x22 x3: 11223.

2.3.4. Однородные и неоднородные линейные рекуррентные соотношения

именуется характеристическим многочленом для возвратной

Используя выражение (10), можно находить очередной член последовательности по предшествующим k членам. В том случае, когда известны начальные значения a0 , a1, ..., ak 1,

можно найти остальные члены последовательности. Соотно-

шение (10) называется однородным линейным рекуррентным соотношением. Для определения общего члена an из форму-

лы (10) используется такой способ. Применяют вспомогательный полином L(t) 1 c1t c2t2 ... cktk и находят произ-

производящая функция последовательности an . Степень

C t не превосходит k 1, поскольку коэффициенты при

tn k , n 0,1, 2,..., будут нулевыми (см. уравнение (8)). В этом случае fa (t) CL tt . Чтобы определить вид формулы общего

члена an , , нужно найти коэффициент при t n в разложении в степенной ряд производящей функции fa (t).

Пример 1. Найти формулу общего члена последовательности an , удовлетворяющей рекуррентному соотноше-

нию an 2 4an 1 3an 0, a0 2, a1 1, n 0, 1, 2,.... .

Решение. Здесь k =2, р1 = - 4, р2 = 3.

49

Выпишем заданное рекуррентное соотношение в виде

(10): an 2 4an 1 3an , n 0, 1, 2, ...; c1 4; c2 3. Вспомога-

тельный полином будет иметь вид: L t 1 4t 3t2.

С t fa t L t ak t k 1 4t 3t 2

k0

a0 a1t ... ant n ... 1 4t 3t 2

a0 a1t ... ant n ... 4a0t

a3 4a2 3a1 t3 L an 4an 1 3an 2 t n

an 1 4an 3an 1 t n 1 an 2 4an 1 3an t n 2

L a0 a1 4a0 t 2 1 4 2 t 2 7t.

A и B найдём методом неопределённых коэффициентов.

50