
Методическое пособие 598
.pdfСвойства планарных графов.
1.Любой подграф планарного графа планарен.
2.Для того, чтобы граф был планарен, необходимо и достаточно, чтобы любая компонента связности данного графа представляла собой планарный граф.
Гранью планарного графа именуется совокупность точек плоскости, всякая пара которых может быть соединена плоской кривой, не пересекающей рёбер данного графа.
Границей грани именуется совокупность вершин и рёбер, имеющихся в данной грани.
~
К примеру, у графа G, изображённого на рис. 53, восемь граней: 1 , 2 , …, 8 . Неограниченная грань 1 назы-
вается внешней, другие грани 2 , …, 8 – внутренними.
Обозначим n, m, f – соответственно количество вер-
шин, рёбер и граней планарного графа.
Теорема Эйлера. Для любого связного планарного графа справедливо утверждение:
n m f 2. |
(39) |
Гомеоморфизм графов. |
|
Рассмотрим операцию подразбиения ребра в |
графе |
G S,U . В результате разбиения ребра (x, y) U образует-
ся |
|
граф |
|
G |
|
|
|
|
, |
|
|
|
|
у |
|
|
которого |
||
|
|
|
S , U |
|
|
|
|
|
|
|
|||||||||
S S |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
xy , U |
U \ |
|
|
x, y |
|
|
|
|
x, xy |
|
, |
|
xy, y |
|
, |
таким об- |
||
разом, вместо ребра |
(x, y) |
получается |
|
(x, y) |
– цепь длины |
||||||||||||||
два.
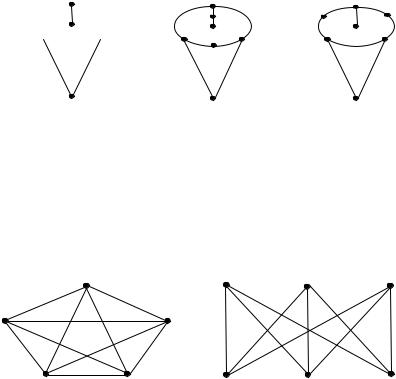
Два графа именуются гомеоморфными при условии, что они оба могут быть построены из одного и того же графа подразбиением его рёбер. На рис. 54 представлены заданный
граф G и два гомеоморфных графа G1 и G2 .
151
G |
G1 |
G2 |
x y
y
Рис. 54. Гомеоморфизм графов
Теорема Понтрягина – Куратовского.
Для того, чтобы граф был планарен, необходимо и достаточно, чтобы он не имел подграфов, гомеоморфных K5 или
K3,3.
K5 |
K3,3 |
Рис. 55. Полные графы
Эквивалентная форма критерия планарности.
Теорема. Для того, чтобы граф был планарен, необходимо и достаточно, чтобы в нём не существовало подграфов, стягиваемых (другими словами, образуемых в результате последовательности отождествлений вершин, связанных рёбра-
ми) к графам K5 или K3,3.
Для непланарных графов определяются характеристики, характеризующие ту или иную степень непланарности. В том случае, когда граф непланарен, то для его графического пред-
152
ставления вычёркивают некоторые рёбра (помещают их на другую плоскость).
Минимальное количество рёбер, в результате вычёркивания которых образуется планарный граф, именуется числом планарности, другими словами, искажённостью sk(G) гра-
фа G.
Теорема. Для числа планарности полного графа верно
утверждение: |
|
sk(G) C2 3n 6, n 3. |
(40) |
n |
|
Толщиной t(G) непланарного графа G именуется ми- |
|
нимальное количество планарных подграфов графа G, |
в ре- |
зультате объединения которых получается заданный граф. Толщина графа равна наименьшему количеству плоскостей l,
при котором граф G распадается на плоские части G1 , G2 ,
..., Gl . Толщина планарного графа равна 1.
Теорема. Для толщины связного n, m – графа верны оценки:
|
m |
|
|
m 3n 7 |
|
|
|
|
t(G) |
|
|
1, |
t(G) |
|
|
, |
(41) |
|
|
|||||||
3n 6 |
|
|
|
3n 6 |
|
|
|
|
где квадратными скобками обозначены целые части данных выражений.
3.7.2. Алгоритм укладки графа на плоскости
Критерии планарности на практике обычно сложны и не позволяют получить информацию о том, как осуществлять укладку графа на плоскости, в том случае, когда он планарен. Данные причины послужили поводом для появления алгоритмов, проверяющих граф на планарность и конструирующих его плоскую укладку. Опишем один из них. Данный алгоритм предлагает процедуру последовательного добавления
~
к некоторому уложенному подграфу G графа G новой цепи
153
L, оба конца которой входят в G. Затем в качестве подграфа
~
G берётся произвольный простой цикл графа G и процедура добавления новых цепей продолжается до получения плоского графа, изоморфного G, или добвление новой простой цепи на определённой стадии будет невозможно, что говорит о непланарности заданного графа G. Определим некоторые понятия. Предположим, что есть какая-то плоская укладка под-
~
графа G графа G.
~ |
~ |
~ |
Сегментом Gi по отношению к G |
S, U именуется |
|
|
|
|
подграф графа G (S,U ) одного из двух видов: |
|
|
~ |
|
~ |
1) ребро u x, y U , такое, что u U , x, y S; |
||
~ |
|
|
2) компонента связности графа G \ G, |
дополненная все- |
|
ми рёбрами графа G, инцидентными вершинам выбранной |
||
компоненты, и концами этих рёбер. |
|
|
Вершина u сегмента Gi именуется контактной при ус-
~
ловии, что u S .
|
~ |
Граф G – плоский, значит, он разделяет плоскость на |
|
грани. |
Допустимой гранью для сегмента Gi по отношению к |
~ |
~ |
G именуется грань графа G, включающая все контактные |
|
вершины сегмента Gi . Пусть Gi – совокупность допустимых граней Gi . Для непланарных графов может оказаться,
что Gi .
Воьмём простую цепь L сегмента Gi , соединяющую
две разные контактные вершины и не имеющую иных контактных вершин. Данного вида цепи именуются -цепями.
154
Любая -цепь допускает укладку в каждую грань, допустимую для данного сегмента.
Два сегмента G1 и G2 именуются конфликтующими в том случае, когда:
1)x1 x2 ;
2)найдутся две -цепи L1 G1 и L2 G2 , которые без
пересечений нельзя уложить вместе ни в какую грань .
~
Предположим, что G – плоская укладка некоторого подграфа графа G. Для каждого сегмента Gi по отношению
~
к G определяем совокупность допустимых граней. При этом возможны такие три варианта.
1. Имеется сегмент Gi , для которого Gi . Тогда
заданный граф G непланарен.
2. Для какого-то сегмента Gi найдётся единственная
допустимая грань . При этом можно поместиь всякую - цепь сегмента Gi в грани . В этом случае грань разделит-
ся на две грани.
3. Gi 2 для Gi . Тогда можно поместиь -цепь в
произвольной допустимой грани.
Алгоритм укладки планарного графа G на плоскость содержит такие шаги:
Шаг 1. Берём произвольный простой цикл C графа. Данный цикл допускает укладку на плоскости и принимается
~
G C.
~
Шаг 2. Определяем все грани графа G и все сегменты
~
Gi по отношению к G . В том случае, когда совокупность сегментов пуста, переходим к шагу 7.
155
Шаг 3. Для любого сегмента Gi находим множество допустимых граней Gi . Если существует сегмент Gi , для которого Gi , то заданный граф G непланарен; окон-
чание работы алгоритма, в противном случае переходим к шагу 4.
Шаг 4. В том случае, когда найдётся сегмент Gi, для которого возможна единственная допустимая грань , перехо-
дим к шагу 6, в противном случае к шагу 5. |
|
|
Шаг 5. |
Для сегмента Gi , у которого |
Gi 1, берём |
любую допустимую грань. |
|
|
Шаг 6. |
Любая -цепь сегмента Gi |
располагается в |
~ |
~ |
|
грани , G заменяется на G L и осуществляется переход к шагу 1.
~
Шаг 7. Произведена укладка G графа G на плоскости.
Окончание работы алгоритма. |
|
Пример 1. |
G |
|
х1 |
х2 |
х3 |
х4 |
х8 |
х7 |
х6 |
х5 |
Рис. 56. Неорграф
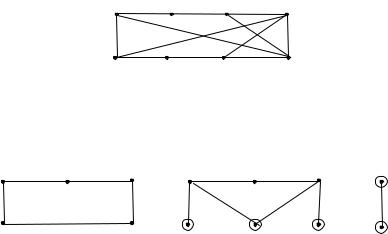
Шаг 1. Берём простой цикл C х1, х2 , х3 , х4 , х5 , разде-
~
ляющий плоскость на две грани 1 и 1 . Примем G C.
~ |
х |
|
х |
х |
|
х |
|
х |
|
х |
|
|
х3 |
G |
|
|
|
|
|
|
|||||||
|
1 |
2 |
3 |
G: |
|
8 |
|
7 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
G: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х5 |
х4 |
х1 |
х4 |
х5 |
х |
|
|
|
5 |
||||
|
Рис. 57. Простой цикл и сегменты |
|
|
|||
|
|
|
|
|||
|
|
156 |
|
|
|
|
|
~ |
Шаг 2. На рис. |
57 показан граф G C и сегменты G1 , |
|
~ |
G2 заданного графа |
по отношению к G . Контактные вер- |
шины заключены в кружки. Gi 1, 2 , i 1, 2.
Шаг 3. Gi , i 1, 2.
Шаг 4. Не существует сегмента, для которого нашлась бы единственная допустимая грань.
|
Шаг 5. Каждая - цепь допускает укладку в 1 или в |
2 . Возьмём для укладки грань 1. |
|
|
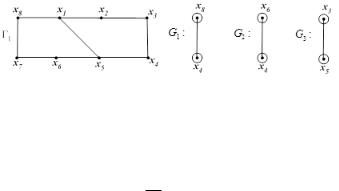
Шаг 6. Пусть L x1, x8 , x7 , x6 , x5 . Расположим данную |
|
~ |
-цепь в 1. Образуется новый граф G и его сегменты G1 , |
|
G2 , G3. Возникает и новая грань 3.
~
G
Рис. 58. Укладка и сегменты
Возвращаемся к шагу 1.
Шаг 1. Образовалось три новых сегмента: G1 , G2 , G3.
Шаг 2. G1 1 , G2 1 , G3 1, 3 .
Шаг 3. Gi , i 1,3.
Шаг 4. G1 G2 1 , переходим к шагу 6.
Шаг 6. |
|
– цепь L1 х4 , х8 расположим в грани Г1, |
– цепь L2 |
х4 , х6 тоже расположим в той же грани. В |
|
|
|
157 |

~
итоге образуется новый граф G . У него 5 граней и один сегмент.
~
G
Рис. 59. Укладка и сегмент
Шаг 1. G1 – ребро x3 , x5 .
Шаг 2. G1 3 . Шаг 3. G1 .
Шаг 4. G1 3 , переходим к шагу 6.
Шаг 6. – цепь L1 х3 , х5 расположим в грани 3.
~
Полученный граф G представляет плоскую укладку заданного планарного графа.
~
G
Рис. 60. Плоская укладка
158
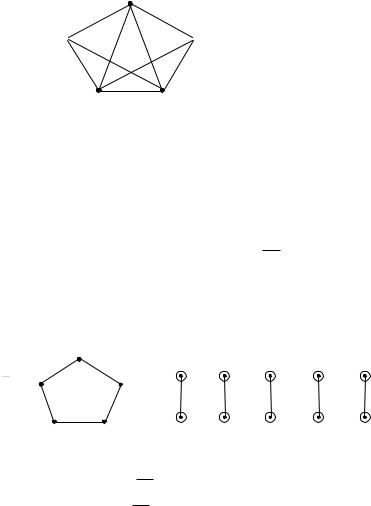
Пример 2.
х3 K5
х2
 х4
х4
х1 х5
Рис. 61. Полный граф K5 .
Попробуем произвести плоскую укладку графа K5 .
Поскольку достоверно, что граф непланарен, алгоритм должен окончить работу на шаге 3.
Шаг 1. Берём простой цикл C xi , i 1, 5 , G~ C.
~
Шаг 2. У графа G две грани: 1 , 2 и пять сегментов, изображённых на приведённом здесь рисунке.
|
|
|
|
х3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
х1 |
х1 |
х2 |
|
х2 |
х3 |
G : |
х |
2 |
|
х4 |
G1 |
: |
G : |
G3 : |
G4 : |
G5 : |
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Г1 |
|
|
|
|
|
|
|
|
|
|
|
|
х |
1 |
х |
|
х3 |
х4 |
х5 |
|
х5 |
х5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
Рис. 62. Простой цикл и сегменты |
|
|
|
||||||
Шаг 3. Gi 2, i 1,5. |
|
|
|
|
|
|
|
||||
Шаг 4. Г (Gi ) 1,i 1,5. |
|
|
|
|
|
|
|
||||
Шаг 5. Берём для G1 и G5 |
грань 2 |
как допустимую. |
|
||||||||
159
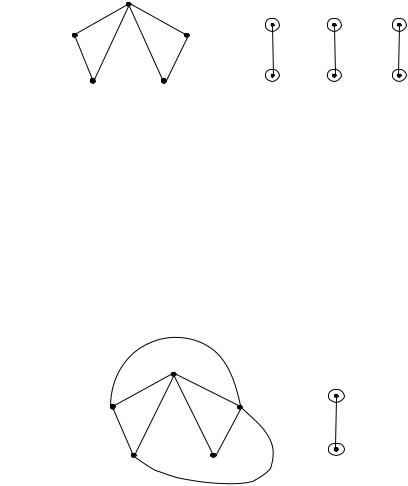
|
|
Шаг 6. -цепи |
|
|
|
L1 х1, х3 и |
L2 |
х3 , х5 добавим к |
||||||||
|
|
~ |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
графу G . Образуется новый граф G и три сегмента G1 , |
G2 , |
|||||||||||||||
G3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х3 |
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
х4 |
|
х1 |
|
х2 |
х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
: |
х2 |
|
Г |
|
Г |
|
|
|
|
|
|
||||
|
G : |
|
|
|
|
2 |
|
|
4 |
|
G1 |
: |
G : |
G3 : |
|
|
|
|
|
|
|
|
|
Г3 |
|
|
|
|
|
|
2 |
|
|
|
|
Г |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
1 |
|
|
|
|
х |
|
х4 |
|
х4 |
х5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
Рис. 63. Укладка и сегменты
~
Шаги 1-2. У графа G четыре грани: 1 , 2 , 3 , 4 .
Шаг 3. G1 1 , G2 1 , G2 1 .
Шаг4. Для G1 |
|
и |
G2 берём грань 1. |
||||||
Шаг 6. – цепи L1 х1, х4 и |
L2 |
х2 , х4 расположим |
|||||||
в грани 1 |
|
|
|
|
~ |
|
|
|
|
и добавим к G . |
|
|
|
|
|||||
|
~ |
|
|
|
|
|
|
|
|
Шаг 1. G и сегмент G1 изображены на рис. 64. |
|||||||||
|
|
|
|
Г5 |
х3 |
|
|
|
|
|
|
|
|
|
|
|
|
х2 |
|
|
|
|
|
|
|
|
|
|
|
G:: |
х2 |
Г2 |
|
Г4 |
х4 |
G : |
|||
|
|
|
|
|
Г3 |
|
|
|
1 |
|
Г |
1 |
|
|
|
Г6 |
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
х |
1 |
|
|
|
х |
|
х5 |
|
|
|
|
|
|
||||
|
|
|
|
|
5 |
|
|
||
Рис. 64. Укладка и сегмент
160
