
Методическое пособие 598
.pdfx1 x2 x3 x4 x5 x6
|
x1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
|
x2 |
|
0 |
0 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|||||||
|
x |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
|
P |
3 |
|
|
|
|
|
|
|
|
|
|
x4 |
0 |
0 |
0 |
0 |
0 |
0 |
|
* |
|
|
x |
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
* |
|
x6 |
|
||||||||
Символом * помечены вершины из множества N0 . Удаляя строки 4 и 6, а также столбцы 4 и 6, получим:
|
x1 |
x2 |
x3 |
x5 |
|
|
|
x1 |
0 |
0 |
0 |
0 |
* |
||
|
|
|
|
|
|
|
|
P x2 |
0 |
0 |
1 |
0 |
. |
||
x |
|
1 |
0 |
0 |
1 |
|
|
3 |
|
|
|
|
|
|
|
x5 |
|
0 |
0 |
0 |
0 |
|
* |
Символом * помечены вершины из множества N1. Удаляя строки 1 и 5, а также столбцы 1 и 5, получим:
|
|
|
x2 |
x3 |
|
|
P |
x2 |
0 |
1 |
|
|
|
x3 |
|
|
|
. |
||
|
|
0 |
0 |
|
* |
|
Символом * помечена вершина из множества N2 . Удаляя строку 3 и столбец 3, получим:
x2
P x2 0 *.
Символом * помечена вершина из множества N3.
111
Построив множества N0 , N1, N2 , N3 , определим значения порядковой функции or x , x X , (на рис. 35 они от-
мечены около вершин). |
|
|
|
Определение. Предположим, что |
g x функция, ста- |
||
вящая в соответствие любой вершине |
xi X |
целое число |
|
g xi 0. Функция g x |
именуется функцией Гранди для |
||
орграфа G, при условии, |
что в любой вершине |
xi значение |
|
g xi есть минимальное из целых неотрицательных чисел, не
входящих в множество g xj : xj xi и g xi 0, когда
xi .
Иначе говоря, g xi представляет собой минимальное из неотрицательных чисел, не соответствующих никакой из вершин xi .
Функция Гранди широко используется при доказательстве многих теорем в теории графов, помимо этого, вычисление некоторых характеристик графа приводит к нахождению значений этой функции.
Пример 2. Определим функцию Гранди для орграфа G из примера 1. Разделим совокупность вершин орграфа на
уровни: N0 x4 , x6 , N1 x1, x5 , N2 x3 , N3 x2 .
Используя определение функции Гранди, получим:
g x4 g x6 0, g x1 g x5 1. Аналогично, |
для верши- |
|||||||||||
ны x3 N2 |
получим: |
|
|
x3 x1, x4 , x5 , |
при |
|
|
этом |
||||
g x4 0, g x1 g x5 1, |
и, |
значит, |
g x3 2. |
Подобным |
||||||||
образом для вершины |
x N |
3 |
получим: |
x x , x , x , |
||||||||
|
|
|
2 |
|
|
|
2 |
3 |
4 |
6 |
||
при этом |
g x |
g |
x 0, |
|
g x 2, |
и, |
значит, |
g x |
|
1. |
||
|
4 |
|
6 |
|
|
3 |
|
|
2 |
|
|
|
112
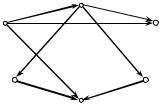
На рис. 36 представлен орграф G , возле всех вершин которого проставлены значения функции Гранди.
2 |
x3 |
|
1 |
|
0 |
|
x4 |
|
x2 |
|
|
|
|
|
1 |
|
1 |
x1 |
0 |
x5 |
|
x6 |
|
Рис. 36. Функция Гранди орграфа
Для орграфов без контуров небольшого порядка используют табличный способ нахождения функции Гранди.
Пример 3. Определим функцию Гранди для орграфа из примеров 1 и 2, применяя табличный способ. Таблица заполняется таким образом:
|
|
|
|
Таблица 2 |
xi |
xi |
g xi |
|
g xj , xj xi |
|
|
|
|
|
x1 |
x6 |
1 |
|
0 |
|
|
|
|
|
x2 |
x3 |
1 |
|
2 |
|
x4 |
|
|
0 |
|
x6 |
|
|
0 |
|
|
|
|
|
x3 |
x1 |
2 |
|
1 |
|
x4 |
|
|
0 |
|
x5 |
|
|
1 |
|
|
|
|
|
x4 |
|
0 |
|
|
|
|
|
|
|
x5 |
x6 |
1 |
|
0 |
|
|
|
|
|
x6 |
|
0 |
|
|
|
|
|
|
|
|
|
|
113 |
|
3.3.Нахождение минимальных путей на орграфах
Алгоритм Дейкстры.
Предположим, что G S,U , орграф с взвешенны-
ми дугами. Пусть s вершина начало пути и t вершина конец пути. Веса дуг должны быть больше нуля.
Этап I. Определение длины минимального пути. Шаг 1. Присвоение вершинам начальных меток.
Присвоим d(s) 0 и считаем данную метку постоянной (постоянные метки отмечаются сверху символом *). Для
других вершин |
xi S, xi s, |
присвоим |
d(xi ) и считаем |
|||||||
|
|
|
|
|
|
~ |
~ |
|
|
|
эти метки временными. Примем x s, x |
имя текущей вер- |
|||||||||
шины. |
|
|
|
|
|
|
|
|
|
|
Шаг 2. Изменение меток. |
|
|
|
|
||||||
Для любой вершины xi |
с временной меткой, непосред- |
|||||||||
|
|
|
|
|
|
~ |
|
|
|
|
ственно следующей за вершиной х |
меняем |
значение её мет- |
||||||||
ки по правилу: |
|
|
x , d x |
x, x . |
|
|||||
d |
|
x min d |
|
|
||||||
|
|
|
|
|
|
~ |
|
~ |
|
|
|
нов. |
i |
|
стар. |
i |
|
|
|
i |
(35) |
|
|
|
|
|
|
|
|
|
|
|
Шаг 3. Превращение метки из временной в постоян-
ную.
Из всех вершин с временными метками берём вершину
x с минимальным значением метки: |
|
j |
|
d x*j min d xj , xj S, d xj временная . |
3.(36).2 |
|
~ |
Считаем данную метку постоянной и полагаем |
x x*. |
|
j |
Шаг 4. Проверка на окончание этапа I. |
|
114
~ |
|
~ |
длина минимального пути от s |
Если х t, |
то d |
х |
|
|
|
|
|
до t. Иначе переходим к шагу 2.
Этап II. Построение кратчайшего пути.
Шаг 5. Последовательный поиск дуг кратчайшего пути.
Из множества вершин, непосредственно предшествую-
~
щих вершине х с постоянными метками, определяем вершину xi , удовлетворяющую соотношению
~ d x
d x |
x , x . |
|
||
|
|
|
~ |
|
i |
|
i |
|
(37) |
|
|
|
|
|
~ |
~ |
|
|
Включаем дугу ( xi , x) в искомый путь и полагаем x xi . |
|
Шаг 6. Проверка на окончаниение этапа II. |
|
~ |
|
Если х s, то минимальный путь получен |
его обра- |
зует последовательность дуг, найденных на пятом шаге и расположенных в обратном порядке. Иначе переходим к пятому шагу.
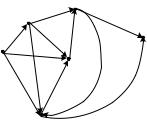
Пример. Пусть имеется сеть G. Определить кратчайший путь из вершины х1 в вершину х6 , используя алгоритм Дейкстры.
|
( ,13 ) |
|
|
х3 |
|
( , 6 ) |
7 |
|
х4 |
||
9 |
|
|
6 |
5 |
|
8 |
( ,15 ) |
(0 ) |
|
х6 |
||||
9 |
|
|
( ,9 ) |
|||
х |
1 |
|
|
|
||
|
|
|
|
х2 |
6 |
|
|
|
|
|
|
||
|
|
11 |
6 |
|
|
|
|
|
|
|
6 |
|
4 |
|
|
|
|
|
|
|
( ,11 )
х5
Рис. 37. Поиск кратчайшего пути на сети
115

Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 x3 |
x4 x5 x6 |
|
|||
|
x1 |
|
9 |
|
6 |
11 |
|
||
|
x |
|
|
|
8 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
6 |
9 |
|
|
3 |
|
|
|
|
|
|
|
. |
|
x4 |
|
5 |
7 |
6 |
|
|||
|
x |
|
|
6 |
|
|
|
4 |
|
|
5 |
|
|
|
|
|
|
|
|
|
x |
|
|
||||||
|
6 |
|
|
|
|
|
|
|
|
Поскольку в исходном графе имеется цикл, проходящий через вершины х2 , х3 и х5 , то вершины графа нельзя упорядочить по алгоритму Фалкерсона.
Этап I.
~
Шаг 1. Присвоим d x1 0* , x x1, d x j , j 2, 6.
Первая итерация.
Шаг 2. Совокупность вершин, непосредственно сле-
~ |
~ |
|
дующих за x x1, с временными метками, |
S x1, x4 , x5 |
. |
Пересчитываем значения временных меток данных вершин. |
||
d x2 |
min , 0* 9 9, d x4 min , 0* 6 6, |
|
5 |
|
|
d x |
min , |
0* 11 11. |
Шаг 3. Одна из временных меток становится постоян-
ной:
~
min d xi , i 2, 6 min 9, , 6, 11, 6* d x4 , x x4.
~
Шаг 4. x x4 t x6 , переходим к шагу 2.
Вторая итерация.
~
Шаг 2. S x2 , x3 , x5 .
116
d x2 min 9, 6* 5 9, d x3 min , 6* 7 13, d x5 min 11, 6* 6 11.
Шаг 3. min d x2 , d x3 , d x5 , d x6
~
min 9, 13, 11, 9* d x2 , x x2.
Шаг 4. x2 x6 , переходим к шагу 2.
Третья итерация.
|
3 |
3 |
|
|
|
|
~ |
, d x |
min 13, 9* 8 |
|
|
Шаг 2. |
S x |
13. |
|||
Шаг 3. |
min d x3 , d x5 , d x6 |
|
|
||
~
min 13, 11, 11* d x5 , x x5.
Шаг 4. x5 x6 , переходим к шагу 2.
Четвёртая итерация.
|
~ |
, d x6 |
min , 11* 4 15. |
|
Шаг 2. |
S x6 |
|||
Шаг 3. |
min d x3 , d x6 |
|
||
|
|
|
~ |
|
min 13, 15 13* d x , x x . |
|
|||
|
|
3 |
3 |
|
Шаг 4. x3 x6 , переходим к шагу 2. |
||||
Пятая итерация. |
|
|
||
|
6 |
6 |
||
|
~ |
, d x |
min 15,13* 4 15. |
|
Шаг 2. |
S x |
|||
|
min d x6 min 15 |
~ |
||
Шаг 3. |
15* , x x6. |
|||
Шаг 4. |
x6 t x6 , х6 |
t х6 , окончание этапа I. |
||
Этап II.
Первая итерация.
Шаг 5. Находим совокупность вершин, непосредствен-
~
но предшествующих x x6 , с постоянными метками
117
~
S x3 , x5 . Проверим для этих двух вершин выполнение со-
отношения (3.3.3): |
|
~ |
* |
9 |
||
d x |
15 13 |
|||||
|
|
|
|
|
|
|
~ |
* |
4 |
d |
x5 |
x5 , x6 . |
|
d x |
15 11 |
|||||
|
|
|
|
|
|
|
d x3 x3 , x6 ,
Вносим дугу x5 , x6 в
~
минимальный путь. x x5 .
|
|
|
|
~ |
s x1, переход к шагу 5. |
|
|
|
|
Шаг 6. |
x |
|
|
||||
|
Вторая итерация. |
|
|
|||||
|
|
|
|
~ |
|
x1, x4 . |
|
|
|
Шаг 5. |
S |
|
|
||||
|
~ |
11 |
|
* |
11 d x1 x1, x5 , |
|
|
|
d x |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
~ |
11 |
|
* |
6 d x4 x4 , x5 . Вносим дугу |
x1, x5 |
в |
|
d x |
6 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
минимальный путь. x x1. |
|
|
||||||
|
|
|
|
~ |
s x1, окончание этапа II. |
|
|
|
|
|
Шаг 6. |
x |
|
|
|||
|
Таким образом, минимальный путь от вершины x1 |
до |
||||||
вершины |
x6 |
найден. Его длина (вес) равен 15, этот путь со- |
||||||
ставляют дуги: |
x1, x5 x5 , x6 . |
|
|
|||||
Алгоритм Беллмана-Мура.
Веса дуг могут быть и меньше нуля.
Этап I. Нахождение длин кратчайших путей от вершины s до всех остальных вершин графа.
Шаг 1. Присвоение начальных значений.
118
|
~ |
~ |
|
d (s) 0, d (xj ) , xj |
s; x s; |
Q x |
совокупность вер- |
шин в очереди.
Шаг 2. Корректировка меток и очереди.
Убираем из очереди Q вершину, стоящую в начале очереди. Для любой вершины хi , непосредственно следующей за
~
x, изменяем значение её метки по формуле
dнов. xi
Если при этом dнов.
min d |
|
x , d |
x |
x, x . |
||
|
|
|
|
~ |
|
~ |
|
стар. |
i |
|
|
|
i |
|
|
|
|
|
|
|
xi dстар. xi , то изменяем порядок оче-
реди вершин, в противном случае продолжаем перебор вершин и изменение значений временных меток.
Корректировка очереди. Если хi отсутствовала ранее в очереди и не находится в ней сейчас, то помещаем её в конец очереди. Если хi уже находилась раньше в очереди или
стоит там сейчас, то поместим её в начало очереди.
Шаг 3. Проверка на окончание этапа 1.
Если Q , то переходим к шагу 2; иначе происходит
окончание этапа, таким образом, кратчайшие расстояния от s до всех других вершин графа определены.
Этап II. Построение кратчайшего пути от s до t.
Идентичен такому же этапу в алгоритме Дейкстры и
|
~ |
|
хi |
~ |
выполняется по формуле d x |
d хi |
, x . |
||
|
|
|
|
|
Пример. Пусть дана матрица весов Ω сети G:
119
|
|
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
|
|
|
|
х |
|
4 |
|
6 |
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
х2 |
|
7 |
8 6 |
|
||||
|
|
х |
|
|
|
|
|
7 |
5 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
х4 |
|
|
|
8 |
|
9 |
|
|
|
|
х |
|
|
|
|
|
|
3 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
х6 |
|
|
||||||
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
х2 |
6 |
|
х5 |
|
|
|
|
|
4 |
|
-8 |
|
|
3 |
|
|
|
|
х1 |
|
|
|
|
9 |
|
|
|
|
|
|
|
7 |
|
-7 |
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
6 |
|
5 |
|
х6 |
|
|
|
|
|
|
|
х4 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х3
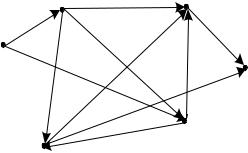
Рис. 38. Сеть с наличием отрицательных весов дуг
Найти минимальный путь от вершины x1 до вершины x6 .
120
