
Методическое пособие 598
.pdf
|
Пример. Задано множество |
|
A x : x |
|
и отноше- |
|||||||||||||||||||||||||||||||||||||
|
|
0,9 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ние |
P |
|
x, y |
|
: x, y A, x |
y |
5 |
|
на |
A . |
В состав отношения |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
P войдут упорядоченные пары: |
|
5,0 |
|
|
, |
|
6,1 , |
|
7, 2 |
|
, |
|
8,3 |
|
, |
|||||||||||||||||||||||||||
9, 4 . В этом случае будем иметь: D = {5, 6, 7, 8, 9}, |
|
R = {0, |
||||||||||||||||||||||||||||||||||||||||
|
|
|
P 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1, 2, 3, 4}, |
|
0,5 |
|
|
, 1,6 |
|
, |
|
2,7 |
|
, |
|
3,8 |
|
, |
|
|
4,9 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Функцией, по-другому, |
отображением из множества A |
||||||||||||||||||||||||||||||||||||||||
в множество |
B |
называется бинарное отношение |
f A B |
|||||||||||||||||||||||||||||||||||||||
при |
условии, |
|
что |
|
|
|
Df |
A , |
|
Rf |
|
B |
|
|
|
и |
|
|
из |
|
|
x, y1 f , |
||||||||||||||||||||
x, y2 f |
y1 |
y2 . |
|
|
Если же имеет место |
|
D f А , |
тогда |
|
f |
||||||||||||||||||||||||||||||||
носит название частичной функции. Для функции |
f |
|
из A в |
|||||||||||||||||||||||||||||||||||||||
B применяется запись |
f : A |
|
B или |
|
|
|
|
|
|
|
f |
|
|
. Тождест- |
||||||||||||||||||||||||||||
|
|
|
А В |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
A |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
венное отношение id |
|
|
|
x, x : x A |
|
|
|
является функцией |
||||||||||||||||||||||||||||||||||
idA : A A , для которой idA x x x A . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Функция f |
именуется инъективной (равнозначной) или |
||||||||||||||||||||||||||||||||||||||||
инъекцией, если отношение |
|
f 1 |
|
является частичной функци- |
||||||||||||||||||||||||||||||||||||||
ей, то есть х1, х2 Df |
, х1 |
х2 , f (х1) f (х2 ) . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
В том случае, когда Rf |
|
B, |
|
функция |
|
f : A B имену- |
|||||||||||||||||||||||||||||||||||
ется |
функцией A на B , иначе говоря, сюръективной функци- |
|||||||||||||||||||||||||||||||||||||||||
ей (по-другому, сюръекцией). |
|
|
|
Сюръекция означает, что |
||||||||||||||||||||||||||||||||||||||
у В х А : f (х) у . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Функция f называется биективной или биекцией, если она является как сюръекцией, так и инъекцией. Другими совами, f осуществляет взаимно-однозначное соответствие
11

между множествами |
A и B . Биективная функция |
f : A A |
||
называется подстановкой множества |
A . Самым простым |
|||
примером подстановки служит функция |
idA . |
|
||
Пример. Даны функции f j |
: A B, j 1, 4. |
|
||
|
f1 |
|
|
|
В |
f2 |
f3 |
|
|
|
f4 |
|
|
|
|
|
|
|
|
|
А |
|
|
|
Рис. 4. Инъекция, сюръекция, биекция |
|
|||
Отображение f1 есть сюръекция, но оно не является инъекцией. Функция f3 представляет собой инъекцию, при этом она не есть сюръекция, отображение f2 – биекция и является подстановкой (если A B ), функция f4 не является ни инъ-
екцией, ни сюръекцией.
Свойства функций.
1) Композиция двух функций есть функция, то есть если f : A B , g : B C , то f o g : A C .
2) Композиция двух биекций есть биекция.
12

3) Функция f : A B имеет обратную функцию
f 1 : B A, если и только если |
f есть биекция, то есть, если |
|||||||
f : A B, то |
f 1 : B A , f o f 1 id |
A |
, |
f 1 o f id |
B |
. |
||
|
|
|
|
|
|
|
||
Характеристической функцией множества A называ- |
||||||||
ется функция |
|
|
|
|
|
|
|
|
|
1, если х А, |
|
|
|
|
|
|
|
|
A x |
х А. |
. |
|
|
|
|
|
|
0, если |
|
|
|
|
|
|
|
Специальные бинарные отношения.
В теории множеств большое значение имеют два вида специальных бинарных отношений: эквивалентности и порядка. Предположим, что имеются конечные множества
A a1, a2 ,..., an и B b1, b2 ,..., bn , и бинарное отношение
Р А В . Зададим матрицу |
|
|
|
P |
|
|
|
|
pij |
бинарного отноше- |
|||
|
|
|
|
||||||||||
|
|
1, |
ai , bj P, |
|
|
|
|
|
|
|
|
||
ния: pij |
|
|
|
|
|
|
|
|
|
||||
|
|
Она отражает связи, существую- |
|||||||||||
|
|
0, |
ai , bj P. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щие между элементами множеств A и B , и даёт возможность проиллюстрировать их графически.
Свойства матриц бинарных отношений.
|
|
|
1) Предположим, что Р, Q А В и |
|
P |
|
|
|
pij |
, |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Q |
|
|
|
|
|
|
|
|
|
, тогда |
|
P Q |
|
|
|
P |
|
|
|
Q |
|
|
|
pij |
|
|
|
qij |
|
|
; |
|
|
||||||||||||||||||||
|
|
qij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
P Q |
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
Q |
|
|
|
|
|
pij qij |
|
, сложение элементов происходит |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
таким образом: 0 0 0 , 1 1 1, 1 0 0 1 1, а умноже-
ние, как 1 0 0 1 0 0 0, |
1 1 1. |
|
|||||||||||||||||||||
2) |
Предположим, что |
Р А В , |
Q В С , тогда |
||||||||||||||||||||
|
P o Q |
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
Q |
|
|
|
, и матрицы перемножаются по традицион- |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
ному правилу умножения матриц, однако произведение элементов при умножении матриц вычисляется так, как указано
вп. 1.
3)
 P 1
P 1 


 P
P
 T , где
T , где 
 P 1
P 1 
 – матрица обратного отноше-
– матрица обратного отноше-
ния P 1 . |
|
|
4) Предположим, что Р Q , |
P |
pij , Q qij , то- |
гда pij qij . |
|
|
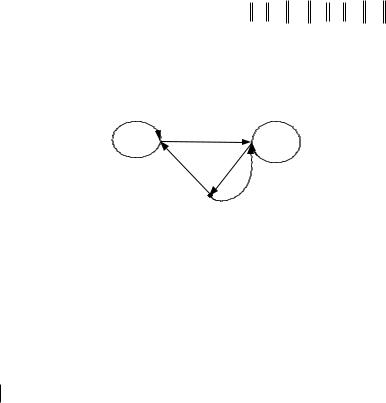
Пример. Бинарное отношение |
Р А2 , А 1, 2, 3 |
|
представлено на рис. 5. |
|
|
2 |
3 |
|
1 |
|
|
Рис. 5. Графическое представление бинарного отношения
|
|
|
|
|
|
0 |
1 |
1 |
|
|
Составим его матрицу: |
|
P |
|
|
|
|
0 |
1 |
|
. Предположим, что |
|
|
|
||||||||
|
|
|
|
|
1 |
|||||
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
||
|
Q |
|
|
|
|
0 |
0 |
1 |
|
, в этом случае |
|
P Q |
|
|
|
P |
|
|
|
|
|
|
|
Q |
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||||||
|
|
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||
Допустим, |
что P – бинарное отношение, заданное на |
множестве A , |
Р А2 . При этом P называется рефлексив- |
|
14 |
ным при условии, |
|
что х А (х, х) Р, таким образом, |
|||||||||
idА Р, |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
... |
|
|
||
|
|
|
|
|
|
1 |
... |
|
|
|
|
|
P |
|
|
|
|
, |
|||||
|
|
||||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
... |
1 |
|
|
|
|
|
|
|
|
|
|
|||||
здесь под символом * подразумевается нуль или единица. Отношение P именуется иррефлексивным при условии,
что х А (х, х) Р .
Отношение P, заданное на множестве A , именуется симметричным при условии, что
х А, у A, (х, у) Р ( y, x) Р. При этом 
 P
P
 T
T 
 P
P
 .
.
Отношение P именуется антисимметричным при условии, что верна импликация
х, у Р у, х Р x y , что означает Р Р 1 idА ,
по-другому, в матричном виде 
 P P 1
P P 1 


 P
P


 P
P
 T . При этом в матрице
T . При этом в матрице 
 P P 1
P P 1 
 все элементы вне главной диагонали
все элементы вне главной диагонали
станут равны нулю, главная диагональ тоже может содержать нули.
Отношение P именуется транзитивным при условии, что верна импликация х, у Р у, z Р x, z Р ,
что означает Р o Р Р.
15

|
|
|
|
|
|
Пример. |
|
Отношение |
P |
|
задано |
|
матрицей |
|||||||||||
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
P |
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 . Каждый элемент главной диагонали матри- |
|||||||||||||||||||
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
цы |
|
|
|
равен единице, таким образом, |
|
P рефлексивно, |
||||||||||||||||||
P |
|
|
|
|||||||||||||||||||||
idA P. |
|
Матрица |
|
P |
|
не является симметрической, таким об- |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
разом, |
|
|
P несимметрично. Выясним, обладает ли P свойст- |
|||||||||||||||||||||
вом антисимметричности. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 1 1 0 |
1 |
1 0 |
1 |
||||
|
P P |
1 |
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
P |
P |
|
|
0 1 1 1 1 |
0 |
|
|
0 1 |
0 |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 1 1 1 |
|
|
|
||||
В данной матрице не все элементы вне главной диагонали равны нулю, таким образом, P не является антисимметричным. Этот пример показывает, что понятие несимметричности отлично от понятия антисимметричности. Выясним, обладает ли P свойством транзитивности.
|
|
|
|
|
|
|
|
1 |
1 |
1 1 |
1 |
1 |
1 1 |
1 |
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
P o P |
P |
P |
P |
|
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
P |
, |
||||
|
|
|
|
|
|
|
|
|
1 |
0 |
|
1 |
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|||||
что означает P o P P, таким образом, P не является тран-
зитивным.
Рефлексивное, транзитивное и симметричное отношение, заданное на множестве A , именуется отношением экви-
валентности |
на A . Обозначение: |
x ~ y. Классом эквива- |
|
лентности |
элемента |
x A |
называется множество |
E x y : x ~ y . |
|
|
|
|
|
16 |
|
Пример. На множестве R действительных чисел зададим отношение a b mod 1 , полагая, что числа a и b равны
по модулю 1 тогда, когда число a b является целым. Из данного определения следует, что каждое число по модулю 1 равно своей дробной части. Каждый класс эквивалентности
будет содержать числа с равными дробными частями. Таким |
||||||||||||||||||
|
|
|
|
|
|
y : y |
|
|
|
|
|
|
|
|
|
|
|
|
образом, E |
|
x |
|
|
x , x R , |
где |
x |
|
– дробная часть |
|||||||||
числа x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разбиением множества |
A называется набор непересе- |
|||||||||||||||||
кающихся подмножеств |
A , таких, что каждый элемент мно- |
|||||||||||||||||
жества A входит в состав только одного из данных подмно- |
||||||||||||||||||
жеств. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Множества 0, |
1 |
3 |
, |
|
1 |
, 2 |
|
и |
2 |
3 |
,1 обра- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
||
зуют разбиение отрезка 0,1 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Отношение P A2 |
именуется предпорядком при усло- |
|||||||||||||||||
вии, что оно одновременно рефлексивно и транзитивно. Используя определения отношения эквивалентности, можно заключить, что симметричный предпорядок есть отношение эквивалентности.
Пример. Дано множество A 1, 2,3, 4 . В этом случае отношение P 1,1 , 2, 2 , 3,3 , 4, 4 , 1, 2 , 3, 2 , 4,1
является предпорядком.
Если для отношения, заданного на множестве A , одновременно выполняются свойства рефлексивности, транзитивности и антисимметричности, то оно именуется частичным порядком на A . Для обозначения частичного порядка ис-
пользуют символ , а обратного ему отношения 1 – символ. Отношение < именуется строгим порядком и задаётся
17
так: x y x y x y . Оно не является частичным
порядком, потому, что не обладает свойством рефлексивности x x.
В тех случаях, когда в множестве A существуют элементы x и y , для которых не представляется возможным говорить, что x y или y x, такие элементы именуют не-
сравнимыми.
Пример. Пусть T – множество положительных делителей числа 30 и есть отношение m n , если m делит n нацело. Целые числа 5 и 15 сравнимы, так как 5 делит 15 нацело, а 5 и 6 – нет.
Частичный порядок именуется линейным порядком при условии, что каждые два элемента x и y , содержащиеся в
множества A , сравнимы, таким образом, x y или y x.
Непустое множество A , на котором задан какой-либо частичный (линейный) порядок, именуется частично (линей-
но) упорядоченным множеством.
Элемент a A , содержащийся в частично упорядочен-
ном множестве A , именуется максимальным (минимальным),
при условии, что x A верна импликация a x x a a x . Элемент a A именуется наибольшим
(наименьшим) при условии, что x a a x x A.
Для наибольшего элемента принята запись max A, наи-
меньшего – min A . Таких элементов множество может не содержать, в частности, в линейно упорядоченном множестве рациональных чисел 0,1 не содержится наименьшего эле-
мента, наибольшим элементом является единица. 18
Замечание. В том случае, когда множество содержит набольший (наименьший) элемент, он является единственным максимальным (минимальным) элементом данного множества.
Пример. Рассмотрим множество точек плоскости с некоторой фиксированной прямоугольной (декартовой) системой координат. Координаты каждой точки плоскости задаются упорядоченной парой x, y действительных чисел. Отно-
шение порядка на множестве точек плоскости определим следующим образом: a,b c, d , если и только если a c
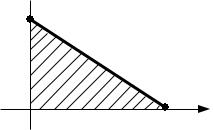
и b d. Рассмотрим множество точек треугольника ОАВ.
у
А
0 |
х |
В |
|
|
Рис. 6. Множество точек треугольника
Точка с координатами 0, 0 является наименьшим элементом этого множества. Максимальными элементами являются все точки, лежащие на стороне отрезка AB . Наибольшего элемента нет.
19
Верхней (нижней) гранью подмножества B частично упорядоченного множества A именуется любой элемент a A : b a a b b B.
Точной верхней (нижней) гранью подмножества B A
именуется наименьшая верхняя (наибольшая нижняя) грань для B . Точная верхняя и точная нижняя грани множества B A записываются как sup B и inf B соответственно.
(супремум) (инфимум)
Примеры. Предположим, что A R.
1)B 3,6 . sup B 6; inf B 3.
2)B 2,5 . sup B 5; inf B 2.
Данные примеры иллюстрируют, что точные верхняя и нижняя грани подмножества могут входить в него, а могут и не входить в него.
Линейный порядок на множестве A именуется полным при условии, что любое непустое подмножество множества A содержит наименьший элемент, тогда множество A
именуется вполне упорядоченным.
Предположим, что имеется конечное частично упорядоченное множество A . Элемент y называется покрываю-
щим элемент x , при условии, что x y и не найдётся такого элемента z , что x z y . В случае x y найдутся такие элементы x1, x2 , ..., xn , что x x1 x2 ... xn y, , где xi 1 покрывает xi . Произвольное частично упорядоченное множест-
во можно отобразить в виде схемы, где всякий элемент представляется точкой на плоскости, и, если y покрывает эле-
20
