
Методическое пособие 598
.pdfРешение. Этап I.
Первая итерация.
~ |
j |
|
|
Шаг 1. x х1, d (х1 ) 0, d (хj ) , |
2, 6, Q х1 . |
||
|
~ |
||
Шаг 2. Q Q \ х1 . Обозначим через S совокуп- |
|||
|
~ |
||
ность узлов, непосредственно следующих за узлом x . |
|||
~ |
4 ? Да. Q х2 . |
||
S x2 , x4 , d x2 min , 0 4 4. |
|||
Узел x2 надо было поместить в конец очереди, но Q было пусто, поэтому конец очереди совместился с началом.
d x4 min , 0 6 6. |
6 8? Да. Q х2 , х4 . |
|
Шаг 3. Q ? Нет. Возврат к шагу 2. |
||
Вторая итерация. |
|
|
~ |
~ |
~ |
Шаг 2. x х2 , Q Q \ |
x |
х4 , S х3 , х4 , х5 ; |
d x3 min , 4 7 11. |
11 ? Да. Q х4 , х3 . |
|
Узел x4 надо поместить в начало очереди, но он уже на- |
||
ходится там. |
|
|
d x5 min , 4 6 10. |
10 ? Да. Q х4 , х3 , х5 . |
|
Шаг 3. Q ? Нет, переход к шагу 2 третьей итера- |
||
ции. |
|
|
Третья итерация. |
|
|
~ |
~ |
~ |
Шаг 2. x х4 , Q Q \ |
x |
х3 , х5 , S х3 , х5 ; |
d x3 min 11, 4 0 4. |
4 11? Да. Q х3 , х5 . |
|
Узел x3 надо помещать в начало очереди, но он уже там находится.
121
d x5 min 10, 4 9 5. 5 10? Да. Q х5 , х3 .
Узел x5 |
перемещаем из конца очереди в начало. |
||
Шаг 3. Q ? Нет, переход к шагу 2 четвёртой итера- |
|||
ции. |
|
|
|
Четвёртая итерация. |
|
||
|
~ |
~ |
~ |
Шаг 2. |
x х5 , Q Q \ x х3 , S х6 ; |
||
d x6 min , 5 3 8. |
8 ? Да. Q х3 , х6 . |
||
Шаг 3. |
Q ? Нет. |
|
|
Пятая итерация. |
|
|
|
|
~ |
~ |
~ |
Шаг 2. |
x х3 , Q Q \ x х6 |
, S х5 , х6 ; |
|
d x5 min 5, 4 7 3. 3 5? Да. Q х5 , х6 . d x6 min 8, 4 5 8. 9 8? Нет.
Шаг 3. Q ? Нет.
Шестая итерация.
|
~ |
~ |
~ |
Шаг 2. |
x |
х5 , Q Q \ x х6 |
, S х6 ; |
d x6 min 8, 3 3 0. 0 8? Да. Q х6 . |
|||
В Q находился один узел x6 |
и он поместился в начало |
||
очереди. |
|
|
|
Шаг 3. |
Q ? Нет. |
|
|
Седьмая итерация. |
|
||
|
~ |
~ |
~ |
Шаг 2. |
x |
х6 , Q Q \ x , S ; |
|
Шаг 3. |
Q . Окончание этапа I. Определены крат- |
||
чайшие расстояния от первого до остальных узлов. Данные
расстояния следующие: d x2 4, |
d x3 4, |
d x4 4, |
122 |
|
|
d x5 3, d x6 0.
Этап II.
|
|
|
|
|
|
|
|
|
|
~ |
|
х6 . |
|
|
|
|
~ |
совокуп- |
|
|
|
|
|
|
Шаг 4. Присваиваем |
x |
|
Обозначим S |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
ность |
узлов, |
непосредственно |
предшествующих |
x . |
||||||||||||||
|
~ |
|
|
x3 , x5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Первая итерация. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
~ |
|
d |
|
0 4 5 d |
х |
|
х , х |
|
|
|
|
|
||||
|
d |
x |
|
х |
|
или |
|
|
|
||||||||||
|
|
|
|
|
|
6 |
|
|
3 |
|
3 |
6 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
d |
|
0 3 3 d |
х х , х |
. |
|
|
|
|||||||
|
d |
x |
|
х |
Вносим |
дугу |
|||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
5 |
5 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 , x6 в минимальный путь. |
|
~ |
|
|
|
|
|
|
|
|||||||||
|
|
x х5 . Переходим к шагу 4. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
~ |
|
|
|
|
|
|
|
Вторая |
итерация. |
|
|
x s ? |
Нет. |
S x2 , x3 , x4 . |
||||||||
|
|
~ |
|
d х |
3 4 7 d х |
|
|
|
; |
|
|
|
|
||||||
d |
x |
|
х , х |
|
|
|
|
||||||||||||
|
|
|
|
|
|
5 |
|
|
|
3 |
|
|
3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
d х |
3 4 6 d х |
|
|
|
; |
|
|
|
|
||||||
d |
x |
|
х , х |
|
|
|
|
||||||||||||
|
|
|
|
|
|
5 |
|
|
|
2 |
|
|
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
d х |
3 4 9 d х |
|
|
|
. |
|
|
|
|
||||||
d |
x |
|
х , х |
|
|
|
|
||||||||||||
|
|
|
|
|
|
5 |
|
|
|
4 |
|
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вносим дугу x3 , x5 |
|
|
|
|
|
|
|
|
~ |
|
||||
|
|
|
|
|
в минимальный путь. |
x х3. |
Пе- |
||||||||||||
реходим к шагу 4. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
~ |
|
|
|
~ |
x2 , x4 . |
|
|
|||
|
|
|
|
|
Третья итерация. x s ? Нет. S |
|
|
||||||||||||
|
|
|
~ |
|
d |
|
4 4 7 d |
х |
|
х , х |
; |
|
|
|
|||||
|
d |
x |
|
х |
|
|
|
|
|||||||||||
|
|
|
|
|
|
3 |
|
|
2 |
|
2 |
3 |
|
|
|
|
|||
|
d |
|
|
|
d х 4 4 8 d х х , х . |
|
|
|
|||||||||||
|
x |
|
|
|
|||||||||||||||
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
4 |
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
123 |
|
|
|
|
|
|
|
||
~
Вносим дугу x4 , x3 в минимальный путь. x х4 . Переходим к шагу 4.
|
|
|
|
~ |
|
|
|
~ |
|
|
|
Четвёртая итерация. x s ? |
Нет. |
S x1, x2 . |
|||
|
~ |
|
d х |
4 0 6 d |
х х , х ; |
|||
d |
x |
|
||||||
|
|
|
4 |
|
1 |
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
~ |
|
d х |
4 4 8 d х |
х , х |
. |
||
d |
x |
|
||||||
|
|
|
3 |
2 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
Вносим дугу x2 , x4 в минимальный путь. x х2 . Переходим |
||||||||
к шагу 4. |
|
|
|
|
|
|||
|
|
|
|
~ |
|
~ |
x1 . |
|
|
|
|
Пятая итерация. x s ? Нет. |
S |
||||
|
~ |
|
d х |
4 0 4 d х |
х , х |
. |
||
d |
x |
|
||||||
|
|
|
2 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
Вносим дугу x1, x2 в минимальный путь. x х1. Переходим |
||||||||
к шагу 4. |
|
|
|
|
|
|||
|
|
|
|
~ |
|
|
|
|
|
|
|
Шестая итерация. x s ? Да. Конец этапа II. Требуе- |
|||||
мый минимальный путь от узла x1 |
до узла x6 имеет вес, рав- |
|||||||
ный нулю, и содержит такие дуги: |
|
|
|
|||||
x1, x2 x2 , x4 x4 , x3 x3 , x5 x5 , x6 .
3.4.Нахождение максимальных путей на орграфах
Алгоритм нахождения максимального пути.
Для определения наибольшего пути граф G (сеть) должен быть ациклическим, иначе может получиться, что длины некоторых путей бесконечны. Пусть задан Gn ацик-
124
лический граф, тогда каждые две его вершины xi x j удов-
летворяют одному из трёх условий: |
xj ; |
||
1) |
xi |
предшествует x j , xi Sпредш. |
|
2) |
xi |
следует за x j , xi Sслед. xj ; |
|
3) нет пути между xi и x j .
Первое и второе условия вместе не могут быть выполнены из-за требуемой ацикличности графа.
Сначала нужно упорядочить вершины графа. Алгоритм нахождения наибольшего пути является перечислительным. Он перебирает все возможные пути от текущей вершины до остальных, достижимых из неё.
Предположим, что d j – длина наибольшего пути от
вершины x1 до вершины x j , в этом случае значение d j |
под- |
||||||
чиняется таким рекуррентным соотношениям: |
|
|
|||||
|
|
|
d1 0, |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d j max(di |
ij : хi Sпред. (х j ), j 2, k 1), |
||||||
|
|
|
|
|
|
|
* |
d j , j |
k 2, n. |
|
|||||
|
|
||||||
Соотношения (*) дают возможность просто определить длины наибольших путей от s x1 до вершин, достижимых из
вершины s. Эти пути могут быть найдены с помощью этапа II алгоритма Дейкстры.
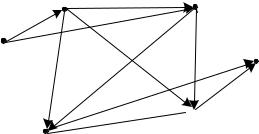
Пример. Граф (сеть, рис. 39) имеет матрицу весов :
125
x1 x1 x2
xx3
4
x5 x6
x2 |
x3 x4 x5 x6 |
|
|||
4 |
|
6 |
|
|
|
|
7 |
8 |
6 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
7 |
5 |
|
|
8 |
|
9 |
|
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
х2 |
8 |
х4 |
|
|
4 |
6 |
|
|
х |
1 |
6 |
9 |
х6 |
|
|
|||
|
7 |
|
|
|
|
|
8 |
|
3 |
|
|
5 |
|
7 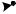 х5
х5
х3
Рис. 39. Сеть
Определить длину наибольшего пути из вершины x1 в x6 и
построить искомый путь.
Решение. Данный граф ациклический, поэтому возможно упорядочение его вершин. Произведём это графическим методом и применим рекуррентные соотношения (*).
126
Рис. 40. Граф с упорядоченными вершинами.
|
Этап I. d1 0, d2 max d1 4 , |
||
d4 |
max d1 |
6, d2 |
8 max 6,12 12, |
d3 |
max d4 |
8, d2 |
7 max 20,11 20, |
d5 |
max d3 |
7, d4 |
9, d2 6 max 27, 21,10 27, |
d6 max d5 |
3, d3 |
5 max 30, 25 30. |
|
Таким образом, длина наибольшего пути из x1 |
в x6 равна 30. |
||
Этап II. |
x6 : d6 30 d5 3 27 3 |
– |
вносим дугу |
x5 , x6 в наибольший путь, |
|
|
|
x5 : d5 27 d3 |
7 20 7 – вносим дугу |
x3 , x5 в наиболь- |
|
ший путь, d5 27 d4 9 12 9, d5 27 d2 |
6 4 6. |
||
x3 : d3 20 d4 |
8 12 8 – вносим дугу |
x4 , x3 в наиболь- |
|
ший путь, d3 20 d2 7 4 7. |
|
|
|
x4 : d4 12 d2 |
8 4 8 – вносим дугу x2 , x4 |
в наибольший |
|
путь, d4 12 d1 6 0 6. |
|
|
|
x2 : d2 4 d1 4 0 4 – вносим дугу x1, x2 |
в наибольший |
||
путь. Таким образом, требуемый путь следующий:
max x1, x2 – x2 , x4 – x4 , x3 – x3 , x5 – x5 , x6 .
127
Особенности алгоритмов теории графов:
1)Любой алгоритм включает набор конечного количества правил и установок. Операции над графами (матрицей), осуществляемые по этим правилам, должны быть достаточно просты;
2)Алгоритм используется в дискретном времени, правила алгоритма − по шагам, количество шагов конечно;
3)Какое из правил будет использовано на текущем шаге или какая операция будет произведена по некоторому правилу, определяется только по результатам предшествущих шагов;
4)Алгоритмы имеют свойство локальности: операция по правилами или доказательство непротиворечивости некоторой операции правилам алгоритма осуществляется при исследовании дуг, инцидентных данной вершине, или вершин, соседних с данной;
5)Алгоритмы имеют свойство массовости: используются или для всех, или для какой-то бесконечной совокупности графов.
3.5.Остовы графов, фундаментальные циклы Деревья (основные определения).
Деревом именуется связной граф, не имеющий циклов. Всякий граф без циклов именуется лесом. Получаем,
что деревья являются компонентами леса. |
|
|
Теорема о дереве. |
|
|
Предположим, что задан граф |
G S,U |
и |
Card S n, Card U m. В этом случае имеет место равносильность следующих заключений.
1)G – дерево.
2)G – связной граф и m n 1.
3)G – ациклический граф и m n 1.
128

4) Каждые две различные вершины графа соединяет только одна простая цепь.
5) G – ациклический граф, удовлетворяющий условию, что если произвольную пару его несоседних вершин соединить ребром, то новый граф будет иметь единственный цикл.
|
х |
х1 |
х4 |
|
х9 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
х3 |
|
|
|
х5 |
|
х7 |
х8 |
х |
х |
|
|
|
|
15 |
|
|
х6 |
|
13 |
|
|
|
|
|
|
||
|
|
х10 |
х11 |
|
х14 |
|
|
|
х |
|
|
|
|
|
|
12 |
|
Рис. 41. Пример дерева
Орграф именуется ориентированным деревом (сокращённо ордеревом), когда:
1)найдётся единственная вершина x1 S, именуемая
корнем, не имеющая имеет предшествующих вершин, таким образом, P x1 0;
2)каждой вершине xj х1 в графе G непосредственно
предшествует единственная вершина, таким образом,
P xj 1.
Неориентированное дерево можно превратить в ориентированное, взяв за корень некоторую вершину.
129
х1 G

 х3
х3
х2 |
х8 |
|
 х9
х9
 х7
х7
х5 х6
Рис. 42. Ордерево
Корень графа G – вершина x6 .
Подграф G (S ,U ) графа G (S,U ) называется ос-
товным подграфом при условии, что S S.
Подграф G графа G именуется остовным поддеревом (другими словами, остовным каркасом), когда S S и G – дерево.
Теорема Кэли.
Количество всевозможных деревьев, построенных на n разных вершинах определяется как tn nn 2 .
Теорема Кирхгофа.
Количество остовных деревьев в связном графе G порядка n 2 равно алгебраическому дополнению (по-другому,
адъюнкте) произвольного элемента матрицы Кирхгофа B G .
Пример.
130
