Методическое пособие 503

Итак, получено выражение для общего решения заданной неоднородной системы:

Y 'º A( x)Y ( x) + b ( x) , Y ( 1) = Y0 .

4.9.Построение фундаментальной матрицы решений однородной линейной системы дифференциальных уравнений

с постоянными коэффициентами методом Эйлера

Рассмотрим линейную однородную систему обыкновенных дифференциальных уравнений n-го порядка с постоянными коэффициентами вида (4.6).

Теорема 4.5. (о фундаментальной матрице решений однородной системы линейных дифференциальных уравнений с постоянными коэффициентами

(метод Эйлера)). Пусть матрица A имеет n различных собственных значений l1 ¹ l2 ¹ K ¹ ln и пусть e1 , e2 ,K, en − соответствующие собственные векторы

Aei = λi ei , (i = 1,2,K, n) ,

тогда фундаментальная матрица решений однородной линейной системы дифференциальных уравнений n-го порядка с постоянными коэффициентами (4.6) имеет вид

F(t ) = e1 × eλ1t , e2 × eλ2 t ,K, en × eλn t .

103

Заметим, что общее решение неоднородной системы с постоянными коэффициентами в этом случае можно записать в виде:

Пример № 4.12. Построим фундаментальную матрицу решений и общее решение линейной системы обыкновенных дифференциальных уравнений 2-го

порядка, которая была решена в примерах 4.8, 4.9: y1 '= y2 ,.y2 '= y1 .

Общее решение системы запишется в виде:

Правильность решения легко проверить подстановкой в исходную систему.

4.10. Устойчивость решений систем дифференциальных уравнений

Любая система дифференциальных уравнений описывает с определенной степенью точности реальный физический процесс.

Приборы, фиксирующие то или иное физическое явление, не совершенны. Может оказаться, что малая погрешность измерения начальных данных вызывает «ощутимые» изменения решений уравнений. В этой ситуации нельзя гарантировать, что выбранная математическая модель реально отражает описываемое ею физическое явление.

И, наоборот, если малые возмущения начальных условий мало изменяют решения на всем промежутке их существования, то соответствующую математическую модель следует признать удачной.

Так возникает важный для приложений вопрос, при каких условиях, математическая модель, описываемая системой дифференциальных уравнений, будет устойчивой.

Рассмотрим систему дифференциальных уравнений

104

Полагаем, что выполнены условия теоремы 4.1 существования и единственности решения задачи Коши.

Пусть некоторое фиксированное решение x = j(t ) этой системы существует

при всех t ³ t0 .

Решение x = j(t ) системы называется устойчивым по Ляпунову при t ³ t0 , если для любого ε > 0 существует число δ > 0 (зависящее от ε) такое, что:

Интегральные кривые и фазовые траектории, отвечающие устойчивым решениям, тоже называются устойчивыми.

На рис. 4.3 сплошной линией изображена устойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка, которая начинается в точке (1,0), и две начинающиеся вблизи её траектории изображены пунктиром.

Рис. 4.3. Устойчивая фазовая траектория, начинающаяся в точке (1,0)

105

Решение x = ϕ(t ) называется неустойчивым по Ляпунову при t ³ t0 , если оно не является устойчивым по Ляпунову, т.е. если существует такое число ε > 0 , что для любого δ > 0 найдутся решения x = xδ (t ) и такое t1 = t1 (δ) , что

xδ (t0 ) - j(t0 ) < d и xδ (t0 ) - j(t0 ) ³ e .

Геометрически это означает, что интегральные кривые x = x (t ) , близкие в момент t = t0 к интегральной кривой x = j(t ) , "удаляются" от неё при t → ∞ .

Интегральные кривые и фазовые траектории, отвечающие неустойчивым решениям, тоже называются неустойчивыми.

На рис. 4.4 сплошной линией изображена неустойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка, которая начинается в точке (0,2; 0), и две начинающиеся вблизи её траектории (пунктирные линии).

Рис.4.4. Неустойчивая фазовая траектория, начинающаяся в точке (0,2;0)

Пример № 4.13. Исследуем на устойчивость решение задачи Коши:

решение устойчиво при t > 0.

Решение системы, проходящее через точку (0, x1(0) , x2(0)), имеет вид

106

Возьмём произвольное ε >0 и рассмотрим поведение при t > 0 тех решений x = x(t ) , которые удовлетворяют условию x(0) − ϕ(0) < δ , где δ = ε > 0 :

x (0) − ϕ(0) = ( x1 (0) − ϕ1 (0))2 + (x2 (0) − ϕ2 (0))2 =

= x1 (0)2 + x2 (0)2 = x (0) < δ

x(t ) − ϕ(t ) = ( x1 (0) − 0)2 + ( x2 (0) − 0)2 = x1 (t )2 + x2 (t )2 =

= ( x1 (0)cost + x2 (0)sin t )2 + ( x1 (0)sin t + x2 (0)cost )2 =

= x1 (0)2 + x2 (0)2 = x (0) < δ = ε.

Последнее неравенство справедливо при всех t > 0 . Получили, что все близкие в начальный момент к точке покоя решения остаются вблизи неё всё последующее время. То есть точка покоя − устойчивое по Ляпунову решение системы.

На рис. 4.5 изображено несколько фазовых кривых системы (это эллипсы). Видно, что те из них, которые начинаются вблизи нуля, всегда вблизи нуля остаются.

Рис. 4.5. Устойчивое по Ляпунову решение системы

107

Пример № 4.14. Исследуем на устойчивость решение задачи Коши

системы ϕ(t ) = 0 , (т.е. ϕ1 (t ) = 0 , ϕ2 (t ) = 0 ).

Докажем, что это нулевое решение не устойчиво при t > 0. Легко видеть, что решение системы, проходящее через точку (0, x1(0) , x2(0)), имеет вид

ряют условию x(0) − ϕ(0) < δ , где δ > 0 :

x (0) − ϕ(0) = ( x1 (0) − ϕ1 (0))2 + ( x2 (0) − ϕ2 (0))2 = x1 (0)2 + x2 (0)2 = x (0) < δ

x (t ) − ϕ(t ) = ( x1 (0) − 0)2 + ( x2 (0) − 0)2 = x1 (t )2 + x2 (t )2 =

= ( x1 (0)cos 4t + x2 (0)sin 4t )2 e0,2t + ( x1 (0)sin 4t + x2 (0)cos 4t )2 e0,2t =

x(t ) − 0 > ε , т.е. тривиальное решение ϕ(t ) ≡ 0 неустойчиво.

108

На рис. 4.6 видно, что фазовые кривые, которые начинаются вблизи нуля, через некоторое время покинут любую окрестность нуля.

Рис.4.6. Неустойчивое по Ляпунову решение системы

4.11. Устойчивость и асимптотическая устойчивость по Ляпунову

Рассмотрим систему дифференциальных уравнений (4.12). Полагаем, что выполнены условия теоремы 4.1 существования и единственности решения задачи

Ляпунову при t ³ t0 , если:

−решение x = ϕ(t ) устойчиво по Ляпунову при t ³ t0 ;

−существует такое число > 0 , что любое решение x = ϕ(t ) ,

удовлетворяющее условию x (t0 ) − ϕ(t0 ) < , с ростом t стремится к нулю:

x (t0 ) − ϕ(t0 ) → 0 при t → ∞ .

Геометрически это означает, что интегральные кривые x = x (t ) , близкие в момент t = t0 к интегральной кривой x = ϕ(t ) , приближаются к ней с ростом t.

Интегральные кривые и фазовые траектории, отвечающие асимптоти-

чески устойчивым решениям, тоже называются асимптотически устойчивыми.

На рис. 4.7 чёрным изображена асимптотически устойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка,

109

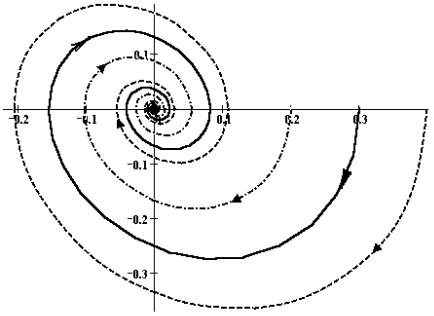
которая начинается в точке (0,3;0), и две начинающиеся вблизи неё, траектории изображены пунктирными линиями.

Рис. 4.7. Асимптотически устойчивая фазовая траектория некой системы дифференциальных уравнений

Пример № 4.15. Исследуем на устойчивость решение задачи Коши

Очевидно, что это решение задачи − тривиальное решение, точка покоя

системы, ϕ(t ) = 0 (т.е. ϕ1 (t ) = 0 , ϕ2 (t ) = 0 ).

Докажем, что это нулевое решение асимптотически устойчиво по Ляпунову при t → ∞ .

Решение системы, проходящее через точку (0, x1(0) , x2(0)), имеет вид: