
Методы оптимального проектирования устройств цифровой обработки и защиты информации. Борисов В.И., Гармонов А.В
.pdf
Q |
|
|
|
|
1 |
M 1 |
|
|
|
|
kn |
||
l |
|
Re |
|
|
|
|
u |
|
(k )R(k ) u |
|
(k )Y (k ) W |
||
pn |
|
M k |
s |
z |
M |
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
0 |
|
|
|
|
|
||||
|
|
|
1 |
|
M 1 |
|
|
|
|
|
(2.33) |
||
|
|
Im |
|
|
|
|
|
us (k )R(k ) u z (k )Y (k ) WM kn , |
|||||
|
M k |
0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
Ql |
|
|
|
|
1 |
M |
1 |
|
|
|
|
kn |
|
|
|
Re |
|
|
|
u |
s |
(k )R(k ) u |
z |
(k )Y (k ) W |
M |
||
qn |
|
M k |
|||||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
0 |
|
|
|
|
|
||||
|
|
|
1 |
|
M 1 |
|
|
|
|
|
(2.34) |
||
|
|
Im |
|
|
|
|
|
us (k )R(k ) u z (k )Y (k ) WM kn , |
|||||
|
|
M k |
0 |
||||||||||
|
|
|
|
|
|
|
|
|
|||||
где us(k) и uz(k) - алгебраические выражения, вид которых зависит от способа задания требований ЧТЗ к ЧХ и не оказывает существенного влияния на объем вычислений.
Выражения в фигурных скобках приведенных формул соответствуют однократному БПФ. С учетом общих членов формул (2.33) и (2.34) компоненты вектора градиента могут
быть в последующем математически обработаны посредством двукратных БПФ.
Данный способ расчета компонент вектора градиента применим также и в случае,
когда одновременно оптимизируются АЧХ и ФЧХ. При этом на практике очень часто вместо ФЧХ одновременно с АЧХ оптимизируется характеристика ГВЗ. В этом случае необходимо член формулы Ошибка! Источник ссылки не найден., соответствующий сумме ошибок ФЧХ обобщенного критерия, преобразовать в сумму ошибок характеристики ГВЗ. При этом в целях ускорения времени расчета характеристики ГВЗ предлагается использовать БПФ.
Представив передаточную функцию НЦФ формулой (2.23) можно получить формулу для
расчета характеристики ГВЗ в удобной для применения БПФ типа (2.25) форме:
|
|
|
|
|
|
|
|
|
Y (k) |
|
R(k) |
|
|
R(k) |
Y (k) |
|
|
||||||
(k) |
1 |
|
|
k |
k |
. |
(2.35) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2M |
|
|
|
|
|
|
|
R2 (k) Y 2 (k) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
F |
|
H ( |
) |
|
|
|
|
|
|
|
|
|
||||||
|
jt h(t) |
|
|
|
, |
|
|
|
|
|
|
|
(2.36) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
F 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где F и F-1 соответственно прямое и обратное преобразование Фурье, то |
|
||||||||||||||||||||||
|
|
|
|
H (k) |
|
|
R(k) |
|
|
|
Y (k) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
k |
|
|
|
|
|
k |
|
|
|
k |
|
|
|
|
|
(2.37) |
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 j (n) |
|
|
|
|
|||||
|
|
|
p |
|
|
|
|
jq |
|
|
|
W |
kn . |
|
|
||||||||
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|||||||||||
|
M |
|
|
|
|
|
|
|
|
M |
|
|
N |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
104
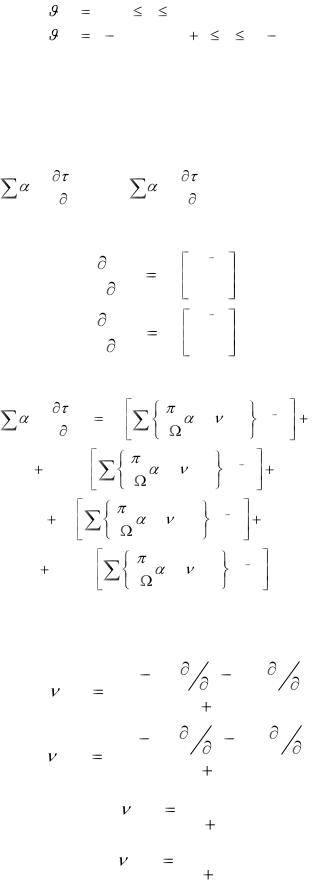
где
(n) |
n, 0 n M / 2 |
(n) |
n M , M / 2 1 n M 1 |
Из формул (2.23) и (2.35) следует, что для быстрого вычисления характеристики ГВЗ целесообразно воспользоваться двукратным БПФ.
Быстрое вычисление компонент вектора градиента связана с необходимостью быстрого вычисления сумм вида:
(k) |
(k) |
и |
(k) |
(k) |
. |
(2.38) |
|
|
|||||
k |
pn |
k |
|
qn |
|
|
Из формул (2.35), (2.37), а также из соотношений
|
|
|
|
R(k) |
|
|
Re |
|
W kn |
|
, |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
||||
|
|
|
|
Y (k) |
|
|
Im |
|
W kn |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
||||
следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k) |
(k) |
Re |
|
|
|
|
|
|
|
(k) |
|
|
(k) W |
kn |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
pn |
2 |
|
|
|
|
1 |
M |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
l(n) Re |
|
|
|
|
|
|
|
|
(k) |
|
|
|
(k) W |
|
kn |
|
||||||||
|
|
|
2 |
|
|
3 |
M |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.39) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
(k) |
|
(k) W |
|
|
kn |
|
|
||||||||
|
|
2 |
|
|
|
|
2 |
M |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
l(n) Im |
|
|
|
|
|
|
|
|
|
(k) |
|
|
|
(k) W |
kn |
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
4 |
M |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При этом
1
2
|
|
(R 2 |
x2 ) |
|
x |
k |
|
2Rx |
R |
||
(k) |
|
|
|
|
|
|
|
k |
|||
|
(R 2 |
|
x2 )2 |
|
|
||||||
|
|
|
|
|
|
||||||
|
|
(R 2 |
x2 ) |
|
R |
k |
2Rx |
R |
|||
(k) |
|
|
|
|
|
|
|
k |
|||
|
(R 2 |
|
x 2 )2 |
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
(k) |
|
|
R |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
|
R 2 |
|
x2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(k) |
|
|
x |
|
. |
|
|
|
4 |
|
|
|
|
|
|
|||||
R 2 |
|
x2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
105

Второй член формулы (2.38) можно получить таким же путем. Из приведенных выше результатов следует, что вычисления по формуле (2.38) целесообразно проводить с использованием четырехкратного БПФ.
Передаточная функция РЦФ имеет вид [72]
m |
|
H (z) C0 H i (z) , |
(2.170) |
i 1 |
|
где |
|
|
|
1 |
a |
z |
1 |
a |
2i |
z 2 |
|
|
|
H i |
(z) |
|
|
1i |
|
|
|
|
. |
(2.41) |
|
1 |
b |
z |
1 |
b |
|
z 2 |
|||||
|
|
|
|
1i |
|
|
2i |
|
|
|
|
Можно показать, что для каскадной формы реализации РЦФ производные АЧХ по его коэффициентам, необходимые при вычислениях по формулам (2.28), (2.29), имеют вид
|
H ( X , ) |
|
|
|
|
H ( X , ) |
|
|
|
[a1i |
(1 a2i ) cos |
] , |
|
|
|
|
(2.42) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
N 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1i |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H ( X , |
) |
|
|
|
|
|
|
H ( X , |
) |
|
|
[ 1 |
2 cos2 |
a |
cos |
a |
|
] |
, |
(2.43) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2i |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
N 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1i |
|
|
|
|
|
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H ( X , ) |
|
|
|
|
|
|
|
|
|
H ( X , ) |
|
|
|
|
|
[b1i |
(1 b2i ) cos |
|
] , |
|
|
|
|
(2.44) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
D 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1i |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H ( X , |
) |
|
|
|
|
|
|
|
|
|
|
H ( X , |
) |
|
|
[ 1 |
2 cos2 |
b |
cos |
|
b |
|
] , |
(2.45) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2i |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
D 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1i |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где
|
|
m |
N |
|
|
|
H ( X , ) |
C |
|
i |
. |
(2.46) |
|
|
|
|||||
0 |
|
|
||||
|
|
Di |
|
|||
|
|
i 1 |
|
|||
Обратимся теперь к численным методам вычисления производных обобщенных критериев оптимальности УЦОС. Достоинством численного подхода, кроме его универсальности, является низкая стоимость подготовки задачи к решению на ПЭВМ. От пользователя требуется лишь написание программы для вычисления значения Q(X ) при заданном X . Для численного расчета первых производных в данной работе использована формула
Q |
|
Q( X s i ) Q( X s i ) |
, |
(2.47) |
xi |
|
2s |
||
|
|
|
где i (0, ,1, ,0) .
106
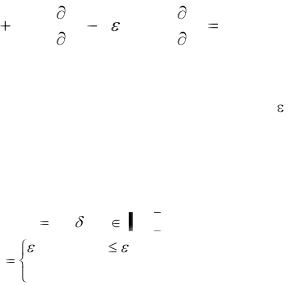
Величина шага s в формуле (2.47) может вычисляться двумя способами. В первом величину s на каждой k+1 -ой итерации определяют в соответствии с известным методом Стюарта [77], и находят как наименьший положительный корень кубического уравнения:
1 |
g 2 |
|
s3 |
|
s2 |
g 2 |
Q |
|
4 |
Qk ( X ) |
Q |
|
0. |
(2.48) |
|
|
|
|
|||||||||||||
|
|
|
|||||||||||||
2 |
ii |
|
|
|
|
ii |
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
i |
|
|
|
i |
|
|
|
Здесь gii - диагональные элементы гессиана обобщенного критерия; Q k ( X ) - значение обобщенного критерия на k-ой итерации;  - машинная точность ( =9.537*10-7). Решение уравнения (2.48) находится способом, изложенным в [77].
- машинная точность ( =9.537*10-7). Решение уравнения (2.48) находится способом, изложенным в [77].
Для ряда алгоритмов величина s является фиксированной в ходе работы и определяется из выражений:
|
s |
i |
x(0) , i |
1, N |
|
|
|
i |
|
|
|
si |
|
i , |
если si |
i |
(2.49) |
si |
в противном случае |
|
|||
|
|
||||
x(0)
где i - i-я компонента вектора начального приближения; - некоторая малая величина.
По результатам тестирования алгоритмов на классе тестовых задач величина принята равной 10-4.
При использовании соотношения (2.47) вычислительные затраты характеризуются числом обращений к вычислению значений Q(X ) : для вычисления градиента – 2N, для вычисления матрицы Гессе - (2N2+1) обращений, где N - размерность вектора варьируемых параметров X .
Эффективность приведенных способов расчета производных была исследована на классе тестовых задач оптимизации УЦОС. Результаты тестирования послужили основой для определения численных значений критериев адаптации при проблемно – адаптивной организации подсистемы расчета производных обобщенных критериев оптимальности УЦОС. К примеру, по результатам тестирования для использованного в данной работе варианта алгоритма соряженных градиентов величину s наиболее целесообразно вычислять как наименьший положительный корень кубического уравнения (2.48).
Отметим, что реализованные на основе численных производных методы оптимизации оказываются, по существу, методами 0 – го порядка [3]. Действительно, заменяя 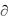
 например, конечно – разностной формулой (2.47), фактически используем лишь значения обобщенного критерия Q , вычисленные при определенных значениях аргумента.
например, конечно – разностной формулой (2.47), фактически используем лишь значения обобщенного критерия Q , вычисленные при определенных значениях аргумента.
107

3. АЛГОРИТМЫ ОПТИМИЗАЦИИ ХАРАКТЕРИСТИК УЦОС
3.1Поисковый алгоритм оптимизации обобщенных критериев
Врассматриваемом случае задача оптимального проектирования УЦОС сводится к решению задачи минимизации скалярной функции полезности. С учетом ограничений на переменные и способов свертывания ЛКО она решается как задача нелинейного программирования (НЛП) с ограничениями [3, 5, 7, 13, 18, 93]
min Q( X ) , |
(3.1) |
X |
|
где в качестве целевой функции используются обобщенные критерии оптимальности, а
область допустимых значений варьируемых параметров D задается двумя типами
ограничений: gi ( X ) 0 , i [1, m]; gi ( X ) |
0 , i [m 1, r]. В общем |
случае функционал |
Q(X ) и функции ограничения gi ( X ) - |
нелинейные, кроме того |
они могут быть и |
негладкими.
Возможные методы решения задачи НЛП типа (3.1) можно разбить на две группы:
методы без вычисления производных (методы 0 – го порядка) и методы, использующие производные (методы 1 – го и 2 – го порядков) [3, 13, 34, 93]. Методы первой группы используются в тех случаях, когда не требуется гладкость и непрерывность целевой функции. Кроме того, их часто применяют на начальном этапе оптимизации, когда требуется выйти в окрестность решения, или получить хорошее начальное приближение. Методы второй группы сходятся намного быстрее и они эффективны на промежуточном и заключительном этапах процесса поиска оптимума.
Рассмотренные в предыдущих главах особенности обобщенных критериев Q(X )
свидетельствуют о том, что для решения задачи (3.1) необходима разработка комбинированного алгоритма оптимизации, в котором должны быть реализованы алгоритмы оптимизации нулевого, первого и второго порядков, глобального и локального поисков. К
идее построения комбинированного алгоритма можно прийти по нескольким причинам. Во-
первых, не существует одного универсального алгоритма минимизации базового набора критериев оптимальности УЦОС. Во-вторых, к этому приводит стремление ускорить сходимость процесса оптимизации, так как на разных этапах скорость сходимости разных методов неодинакова. В-третьих, к этому приводит необходимость решения
108

многоэкстремальных задач. В четвертых, комбинированный алгоритм потенциально обладает способностью адаптироваться под рельеф разных целевых функций Q(X ) .
Для выбора методов решения задачи НЛП (3.1) целесообразно воспользоваться методикой, предложенной в [3]и развитой в работах [25, 53], которая позволяет провести тестовые испытания алгоритмов и программ оптимизации и с большой степенью достоверности отобрать коллектив наилучших конкурирующих алгоритмов. При практических исследованиях, для выбора коллектива оптимизирующих алгоритмов 0 – го порядка, сравнивались программы, реализующие алгоритмы Гаусса – Зейделя, различные варианты случайного поиска, деформируемого многогранника, Флетчера – Пауэлла, попарно
– координатного спуска [3, 7, 12, 23, 26, 30, 35, 41, 62, 74, 93]. Наилучшими оказались вариант поискового алгоритма, предложенного автором, метод деформируемого многогранника (ДМ) и метод статистического градиента (СГ). Поскольку алгоритмы методов ДМ и СГ претерпели при реализации лишь незначительные модификации, то в данном
пункте рассматривается только особенности поискового алгоритма.
Суть предлагаемого алгоритма поискового метода (ПМ) 0-го порядка заключается в проведении серии пробных испытаний критерия Q(X ) и сокращении по результатам пробных испытаний области поиска экстремума за счет исключения из рассмотрения тех
участков области допустимых значений варьируемых параметров, в которых значения Q(X )
оказались большими некоторого порогового для данного шага оптимизации уровня [41]. При этом учитываются ограничения, накладываемые на варьируемые параметры и выходные характеристики в различных точках допустимой области изменения варьируемых параметров. В результате происходит постепенная локализация области решения до определения точки оптимума.
Для работы алгоритма необходимо определить способ вычисления значений обобщенного критерия Q(X ) , задать границы диапазонов изменения варьируемых
параметров X i min и X i max , i [1, K] и значение начального порогового уровня Qn(0) .
Поиск минимума функции Q(X ) с помощью предлагаемого алгоритма осуществляется следующим образом. На каждом шаге поиска K раз ( K - размерность выборки) оценивается величина целевой функции Q( X (k ) ) , i [1, K] . Составляющие каждого
из векторов генерируются из области допустимых значений варьируемых параметров. Для каждого значения Q( X (k ) ) проверяется выполнение условия Q( X (k ) ) Qn(k ) , где Qn(k ) -
109

пороговое значение обобщенного критерия на k -ом шаге. При выполнении этого условия испытание считается успешным.
По всем успешным испытаниям проводится учет соответствующих им величин
целевой функции и значений варьируемых параметров с тем, чтобы определить наименьшее
значение |
целевой |
функции Q(k ) |
и границы |
изменения |
на |
успешных |
испытаниях |
|||||||||
|
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
варьируемых параметров ( X i(maxk ) |
и X i(mink ) |
, i |
[1, N]). На следующем (k |
1) |
шаге оптимизации |
|||||||||||
пороговое (k |
1) значение целевой функции полагается равным Q(k |
1) |
Q(k ) |
, а диапазоны |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
min |
|
|
|
изменения варьируемых параметров - |
X i |
[ X i(maxk ) |
, X i(mink ) ], i |
[1, N]. При этом происходит |
||||||||||||
уменьшение области поиска (локализации экстремума). |
|
|
|
|
|
|
|
|
||||||||
Метод можно отнести к методам поиска глобального экстремума, |
так как если на k - |
|||||||||||||||
ом шаге |
оптимизации наименьшим |
|
оказалось значение Q(k ) |
из |
области |
локального |
||||||||||
|
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
минимума, то |
из-за отсутствия связи |
между Q(k ) |
и центром |
распределения |
пробных |
|||||||||||
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
|
значений |
X i , |
на |
следующем |
шаге |
будут моделироваться |
значения |
X i |
и |
из |
области |
||||||
глобального минимума [24], т. к. они обязательно попадут в область допустимых значений
X (k ) .
Поиск экстремума с помощью метода прекращается, если выполняются условия:
|
|
|
|
|
Q(k ) |
|
|
|
|
|
(3.2) |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(k ) |
|
Q(k 1) |
|
(k ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n |
|
n |
|
|
i |
(3.3) |
|
|
|
|
|
|
|
|
(k ) X |
i |
2 |
, |
|
i [1, N ], |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
(k ) |
X i |
(k ) |
(k ) |
; -максимально допустимая величина целевой функции; |
(k ) |
и 2 |
- |
||||||
|
X i max |
X i min |
1 |
|||||||||||
минимально допустимые величины уменьшения целевой функции и интервалов изменения варьируемых параметров.
Останов по соотношению (3.2) означает, что решение задачи оптимизации найдено с заданной точностью. Выполнение условий (3.3) показывает, что поиск оптимума с помощью рассматриваемого алгоритма исчерпал себя, хотя решение и не найдено. При этом произошла либо потеря области экстремума, либо останов в точке локального оптимума или седловой точке.
Константы , 1, 2 необходимо выбирать осмотрительно, так как от них существенным образом зависит количество оценок Q(X ) , затраченных на поиск экстремума,
110

время решения задачи и успешность поиска в целом. Экспериментальные исследования показывают, что вполне удовлетворительными являются следующие значения этих констант:
(k ) |
0.01Q(k 1) |
, |
|
|
|
1 |
n |
|
|
|
|
|
|
X (0) |
|
||
2 |
0.01max |
X (0) |
. |
||
i |
|
i max |
i min |
|
|
|
|
|
|
|
|
Значение выбирается с учетом необходимой точности получения решения данной |
|||||
экстремальной задачи. |
|
|
|
|
|
Использование алгоритма для решения практических задач оптимизации характеристик УЦОС показывает [41], что при помощи рассматриваемого алгоритма область оптимума локализуется достаточно быстро (15-20 шагов). Но внутри ее сходимость очень сильно замедляется и конечный результат оптимизации за приемлемое число оценок целевой функции Q(X ) удается получить редко. Этот результат практического исследования алгоритма является вполне закономерным и лишний раз иллюстрирует особенности
алгоритма данного типа.
Следует отметить ряд особенностей рассматриваемого алгоритма, оказывающих существенное влияние на его работу.
Количество шагов оптимизации и число выполняемых на них оценок Q(X ) ,
необходимых для уменьшения целевой функции до требуемой величины, в значительной степени зависит от числа испытаний Nis , проводимых на каждом шаге поиска.
Так, при Nis <100, процесс поиска экстремума часто прекращается в результате потери области оптимума. В тех же случаях, когда этого не происходило, на поиск решения необходимо было затратить почти такое же суммарное количество вычислений целевой функции Q(X ) , как при Nis =100 или при Nis =125. При размерности выборки Nis >170
область оптимума не терялась, однако в большинстве случаев на поиск затрачивалось в среднем на 100-200 оценок целевой функции Q(X ) больше, чем при Nis =100 или Nis =125.
Количество шагов оптимизации оставалось при этом прежним. Это можно объяснить следующим причинами.
Существенное сокращение области поиска происходит на первых шагах оптимизации.
Поэтому для случая, когда начальное число испытаний в серии невелико (30-70), а
допустимая область достаточно широка, плотность распределения испытаний будет низкая,
и возможна потеря области допустимых решений. На последующих шагах оптимизации область допустимых значений варьируемых параметров существенно сужается и число оценок Q(X ) может быть уменьшено по сравнению с первоначальным, практически без
111

увеличения вероятности потери области решения. Это подтверждается также тем обстоятельством, что при Nis >170 результаты оптимизации исследуемых УЦОС в смысле суммарного количества оценок целевой функции Q(X ) были хуже, чем при Nis =100..170.
Наиболее оптимальным оказался размер выборки порядка 100 – 170, а допустимая степень
уменьшения Nis в процессе оптимизации равна 15-20% [41].
Когда точка оптимума находится вблизи границ допустимой зоны, рассматриваемый алгоритм работает несколько хуже, т. к. увеличивается вероятность потери области экстремума. Существует несколько приемов выхода из подобных ситуаций [30]. В алгоритме с этой целью проводились дополнительные испытания в граничных точках интервалов изменения варьируемых параметров. При этом, если они оказывались успешными, то границы включались в область допустимых значений варьируемых параметров на
следующем шаге оптимизации [41].
Весьма существенным является выбор начального порогового значения целевой
функции Qn(0) . Чрезмерное уменьшение Qn(0) увеличивает вероятность потери области
оптимума, даже при проведении большого количества испытаний на каждом шаге поиска
экстремума. В то же время выбор заведомо большого не дает существенного
уменьшения области поиска оптимума на первом шаге оптимизации, который в этом случае
сводится лишь |
к выбору |
более |
корректного |
Q(0) . |
Поэтому |
при использовании |
||
|
|
|
|
|
n |
|
|
|
рассматриваемого |
алгоритма |
величина Q(0) |
выбирается |
на основе |
оценок |
начального |
||
|
|
|
n |
|
|
|
|
|
значения целевой функции Q( X (0) ) |
с помощью эмпирических соотношений, |
полученных |
||||||
путем решения тестовых задач. Эти соотношения организованы в виде правил продукции в соответствии с рекомендациями, приведенными в [82].
Необходимо выделить случай, когда среди Nis испытаний, проведенных на текущем шаге оптимизации, нет успешных. Это бывает, когда допустимая область оказывается
значительно больше интервала, в котором выполняется условие Q(X (k ) ) Qn(k ) , что может
привести к потере области оптимума. В этой ситуации целесообразно повторить шаг,
увеличив пороговое значение Q(k 1) . Чаще всего : |
|
||
n |
|
|
|
Q(k 1) |
Q(k ) |
Q(k ) / 2. |
(3.4) |
n |
n |
n |
|
112

Увеличение Qn(k ) согласно соотношению (3.4) происходит до тех пор, пока число успешных испытаний не превысит допустимого минимума Kmin. При исследовании рассматриваемого алгоритма использовалось значение Kmin=6.
Существенна для работы алгоритма оказывается эффективность генератора равномерно распределенных случайных чисел. От того насколько равномерно значения
векторов X (jk ) , j [1, N] располагаются по всей допустимой области, зависит правильность
принятия решения о сокращении области поиска. В практической процедуре поискового алгоритма используется генератор ЛП -последовательности [84, 85], обладающий на сегодняшний день наилучшим свойством равномерного покрытия области. Генерация точек
ЛП -последовательности |
ij |
осуществляется |
в |
работе арифметическим алгоритмом, |
||
|
|
|
|
|
|
|
описанным в [85]. Для перевода точки |
ij j |
в |
произвольный гиперпараллелепипед, |
|||
задаваемый параметрическими ограничениями, используется линейное преобразование: |
||||||
|
X i( j ) |
X нi |
ij ( X вi |
X нi ). |
(3.5) |
|
Если границы вариации параметров имеют значительный разброс и отличаются друг от друга на несколько порядков, то для обеспечения попадания пробных точек в пограничные области будем применять логарифмическое преобразование границ вариации и
варьируемого вектора:
X i( j ) 10lg X нi  ij (lg Xвi lg X нi ).
ij (lg Xвi lg X нi ).
Схема алгоритма поискового метода оптимизации обобщенных оптимальности приведена на рис. 3.1.
Эффективность рассмотренного алгоритма практически не зависит от количества варьируемых параметров и от положения начальной точки поиска (только определение
Qn(0) ). Даже в худших случаях (большое число варьируемых параметров, значительная удаленность начальной точки поиска X(0) от оптимума) алгоритм обеспечивает поиск области решения с достаточно высокой точностью и скоростью. Особо следует отметить, что при этом ищется область глобального оптимума. Это создает все предпосылки для успешного использования алгоритма на первых шагах поиска оптимума при решении задач параметрической оптимизации УЦОС.
3.2 Алгоритм минимизации среднестепенных критериев оптимальности
УЦОС
113
