Методическое пособие 484
.pdf
|
1 |
Начало |
|
|
|
|
|
|
2 |
|
|
|
Требуется справка о работе программы? |
Нет |
|
|
|
||
|
|
Да |
|
3 |
|
|
|
|
|
Справка |
|
22 |
|
|
|
|
4 |
|
|
|
|
|
Нет |
|
Продолжить работу? |
Останов |
|
|
|
Да |
|
5 |
|
|
|
|
Задайте признак обобщенного критерия |
|
|
6 |
|
|
|
|
Задайте размерность задачи |
|
|
21 |
|
|
|
7 |
|
|
|
|
Задайте координаты исходной точки |
|
|
|
8 |
|
|
|
Требуются рекомендации? |
Нет |
|
|
|
||
9 |
|
Да |
|
|
|
|
|
|
Рекомендации по выбору метода |
|
|
20 |
|
|
|
|
|
10 |
|
134
9 |
10 |
Задайте метод |
11 |
Нет |
Градиент используется? |
Да |
12 |
Задайте метод вычисления градиента |
13 |
Ввод необходимых параметров |
20 |
14 |
Да |
Начать счет? |
Нет |
15 |
Да |
Хотите изменить параметры? |
Нет |
16 |
Промежуточные результаты |
17
135
16
17
Нет
Требуются рекомендации?
Да
18
Рекомендации по дальнейшим действиям
19
Да
Продолжить поиск из полученной точки?
Нет
20
10 Продолжить поиск из полученной точки?
|
Да |
|
|
14 |
|
|
|
21 |
7 |
Да |
Начать поиск из новой точки?? |
|
||
|
22 |
Нет |
|
|
|
4 |
|
Конечный результат |
23
Конец
Рис. 3..4. Схема алгоритма организации маршрута процесса оптимизации УПОС
136
|
Начало |
|
|
Задание начальных значений точек альтернанса на |
|
|
основе аналитического решения задачи |
|
|
аппроксимационного синтеза |
|
|
Решение задачи чебышевской интерполяции |
|
|
Чебышевский альтернанс получен? |
Да |
|
|
|
|
Нет |
|
|
Замена точек альтернанса |
|
Нет |
Проводить выравнивание максимумов? |
|
|
|
|
|
Да |
|
|
Выравнивание максимумов валле-пуссеновского |
|
|
альтернанса |
|
|
Выдача оптимального решения |
|
Конец
Рис. 3.5 Схема алгоритма второго модифицированного метода Ремеза
137
Способы вычисления весовых коэффициентов
|
|
|
|
|
На основе |
|
|
|
|
|
|
|
|
|
теоретико- |
|
|
|
|
|
|
|
|
|
игровой |
|
|
|
|
На основе |
|
С |
По |
|
модели |
|
На основе |
|
На основе |
опыта проекти |
|
использованием |
коэффициентам |
|
|
|
«энтропийной» |
|
решения задачи |
ровщика |
|
ЛП - последова |
относительного |
|
|
|
модели |
|
линейного прог |
|
|
тельностей |
разброса ЛКО |
|
|
|
|
|
раммирования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.6 Методы вычисления весовых коэффициентов
138
4. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ОПТИМАЛЬНОГО
ПРОЕКТИРОВАНИЯ
4.1 Оптимизация частотных характеристик устройств цифровой обработки
сигналов нерекурсивной структуры
В наиболее широкой постановке задача оптимизации ЧХ НЦФ заключается в
получении АЧХ и ФЧХ, описываемых передаточной функцией
N 1 |
|
|
H ( X , j ) |
b e j T , |
(4.1) |
|
i |
|
i |
0 |
|
где bi, i=1,2…N-1 – коэффициенты передаточной функции, удовлетворяющие заданным ограничениям (см. рис. 4.1).
Здесь HB( ) и HН( ) – ограничения сверху и снизу на вид желаемой АЧХ, B( ) и
Н( ) – ограничения сверху и снизу на вид желаемой ФЧХ.
Математически эту задачу можно записать в виде
H H ( ) |
H ( X , ) |
H B ( |
) |
H ( ) |
( X , ) |
B ( ) |
(4.2) |
|
НВ( |
) |
|Н(Х,j )| |
|
НН( |
) |
а) |
|
В( |
) |
|
|
|
(Х,j ) |
|
Н( |
) |
|
б) |
|
Рис. 4.1. Типовая постановка задачи оптимизации синтеза НЦФ:
а) ограничения на АЧХ; б) ограничения на ФЧХ
что приводит к необходимости решения системы неравенств вида
102
g1 X , |
H B |
|
H X , j |
|
0, |
|||
g2 |
X , |
H H |
|
|
H X , j |
|
0, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
(4.3) |
g3 |
X , |
B |
arg H X , j |
0, |
||||
g4 |
X , |
H |
|
arg H X , j |
0, |
|||
В наиболее общем случае ограничения Ошибка! Источник ссылки не найден.
нелинейны относительно своих параметров Xi, i=1,2…N, поскольку
|
N 1 |
H X , j |
X i cos 2 i |
|
i 0 |
arg H ( X , j ) 
arctg
2 |
N 1 |
2 |
|
|
X i sin 2 i
i 0
N 1
X i sin 2 i
i 0
N 1
X i cos 2 i
i 0
(4.4)
(4.5)
Решение системы нелинейных уравнений (4.3) сведем к решениям соответствующей задачи нелинейного программирования (НЛП) без ограничений [ ]. Функция штрафа в задаче (НЛП) будет иметь вид
|
P |
|
Q X , |
n F gi X , , |
(4.6) |
|
n 1 |
|
где i 0 - представляют собой весовые коэффициенты;
F[gi(X, )] - функционал, который выбирается с учетом требований:
F gi |
X , |
0, если gi |
X , |
0 |
|
|
|
|
(4.7) |
F gi |
X , |
0, если gi |
X , |
0 |
Существуют различные штрафные функции для решения задач оптимизации.
Наиболее часто используются функции Розенброка, Вейсмана, Кэрояка. Вид используемой штрафной функции определяется особенностями решаемой задачи.
Достоинством предлагаемого подхода к оптимизации НЦФ заключается в том, что за счет перехода от задачи Ошибка! Источник ссылки не найден. к задаче минимизации без
103
ограничений значительно упрощается процедура вычислений, что особенно важно если учесть большую размерность решаемой задачи.
Покажем возможность применения оптимального подхода к решению задач оптимизации НЦФ с линейной ФЧХ. В качестве начального приближения возьмем фильтр,
коэффициенты которого рассчитываются по формуле
b |
sin X |
, |
|
||
l |
X |
|
|
||
где N = ?
В качестве штрафной функции используем модифицированную функцию Вейсмана,
которая будет иметь вид
|
|
M |
4 |
|
|
|
|
Q( X , |
) |
|
Wi gi ( X , j ) |
(4.8) |
|||
|
|
j 1 i 1` |
|
|
|
||
где |
|
|
|
|
|
|
|
Wi |
1, если gi ( X , |
j ) |
0 |
(4.9) |
|||
Wi |
0, если gi ( X , |
j ) |
0 |
||||
|
|||||||
Для минимизации функции применим комбинацию метода ЛП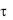
- поиска и Давидона-
Флетчера-Пауэлла (ДФП) [ ], согласно которому минимизация осуществляется по итерационной схеме
X i 1 X i i H i Q( X i ) |
(4.10) |
Градиент Q( X ) определяется как
|
Q |
|
|
X1 |
|
|
Q |
|
Q( X ) |
X 2 , |
(4.11) |
|
... |
|
|
Q |
|
|
X N |
|
а гессиан вычисляется по формуле
H i 1 H i |
Bi BiT |
|
H iT i iT H i |
, |
(4.12) |
BiT i |
|
iT H i i |
|||
|
|
|
|
104
где i - определяется путем одномерного поиска:
i |
Q( X i 1 ) Q( X i ), |
|
|
|
(4.13) |
Bi |
i H i |
Q(ci ) |
На рисунке 4.2 представлена АЧХ оптимизированного НЦФ полученная после 50
итераций ЛП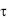
- поиска и 14 итераций ДФП. Из рисунка видно, что оптимизированная АЧХ НЦФ полностью находится в зоне, заданной ограничениями. АЧХ фильтра начального
приближения рассчитывались по формуле sin X .
X
Вприложении 3 приведены коэффициенты передаточной функции.
4.2Оптимизация частотных характеристик устройств цифровой обработки
сигналов рекурсивной структуры
В программе оптимизационного проектирования цифровых фильтров (ЦФ) с
произвольными амплитудно-частотными характеристиками (АЧХ), приведенной в работах
[3,4], в качестве метода оптимизации используется метод Давидона-Флетчера-Пауэлла
(ДФП), обладающий рядом недостатков. В работе описывается алгоритм и программа,
построенные на основе метода сопряженных градиентов с улучшенной обусловленностью,
позволяющая существенно сократить вычислительные затраты при проектировании ЦФ со сложными АЧХ.
Задача проектирования РЦФ со сложной АЧХ (многополосные фильтры,
дифференциаторы и т. п.) решается с помощью оптимизационных методов,
минимизирующих целевую функцию вида
|
N |
2W n , |
|
||
Q X , K * |
K * |
H X , n |
A n |
(4.14) |
|
|
n 1 |
|
|
||
где X – вектор коэффициентов a1i, a2i, b1i, b2i передаточной функции ЦФ H(z), представленной
|
|
|
|
M |
1 |
a |
z 1 |
a |
2i |
z 2 |
|
|
|
в каскадной форме H (z) K i 1 |
|
1i |
|
|
|
; |
|||
|
|
1 |
a1i z 1 |
a2i z 2 |
|||||||
|
H X ,Wn |
|
- модуль H(z) АЧХ ЦФ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A( |
n) – эталонная АЧХ; |
|
|
|
|
|
|
|
|||
W( |
n) – весовая функция характеризующая «значимость» n–й точки эталонной АЧХ; |
||||||||||
105
N |
|
N |
2 . |
|
K * |
H X , n |
A n / |
H X , n |
|
n 1 |
|
n 1 |
|
|
Функция (4.14) непрерывна, ее производные по элементам вектора X легко вычисляются в аналитическом виде и также являются непрерывными функциями [4,6]. Это позволяет применить позволяет применить для минимизации функции (4.14) наиболее эффективные методы нелинейного программирования, использующие производные.
Наиболее широко используется метод ДФП, поскольку при решении широкого класса задач он является одним из самых эффективных [5] и реализующие его программы имеются в стандартном математическом обеспечении большинства ЭВМ. Основным недостатком данного метода является то, что для овражных целевых функций аппроксимация обратной
106