
Методическое пособие 484
.pdf
задача скалярной оптимизации будет сформулирована в виде задачи минимаксной аппроксимации, а именно, подставляя (2.4) в (2,5) имеем
min max e( X , ). |
(2.6) |
XE
Вобщем случае аналитическое решение задачи (2.3) неизвестно. Для численных
методов расчета характеристик устройства необходимо перейти к дискретной задаче путем
покрытия области E |
-сетью с дискретными значениями |
1, |
2,…, |
Р. Если обозначить |
f j ( X ) Hi ( X , l ) , Z1 j |
Hнi ( l ) , Z2 j Hвi ( l ) , [1, Pi ], |
i |
[1,P], |
где Pi - количество |
точек в поддиапазоне E i , то соответственно условия работоспособности будут определяться соотношениями
Z1 j f j ( X ) |
Z2 j , j [1, M ], |
(2.7) |
и |
|
|
Qj (X ) |
e j (X , ) , |
(2.8) |
а дискретная минимаксная задача, следующая из исходной непрерывной задачи (2.3), может быть сформулирована в виде задачи скалярной оптимизации Ошибка! Источник ссылки не найден., где
|
|
|
Q( X ) |
max Qj ( X ) |
(2.9) |
||
|
|
|
|
|
j [1,M ] |
|
|
или в виде |
|
|
|
|
|
|
|
|
|
|
min max Qj ( X ) |
(2.10) |
|||
|
|
|
|
X Ew |
j [1,M ] |
|
|
Таким образом, задача векторной оптимизации фактически сведена к задаче |
|||||||
скалярной оптимизации, решение которой связано с минимизацией M функции максимума |
|||||||
(2.9), заданной на EN. |
|
|
|
|
|
|
|
В случае, когда критерий Q(X ) задан на всем пространстве EN, имеем следующие |
|||||||
выражения для непрерывных и дискретных задач скалярной оптимизации |
|
||||||
|
|
|
|
min Q( X ), |
(2.11) |
||
|
|
|
|
X |
D |
|
|
|
|
|
min max e( X , ), |
(2.12) |
|||
|
|
|
X |
D |
E |
|
|
|
|
|
|
min max Q j ( X ). |
(2.13) |
||
|
|
|
|
X D |
j [1,M ] |
|
|
Нередко в качестве обобщенного критерия выбирается среднестепенная норма |
|||||||
|
|
|
|
|
M |
|
|
|
|
|
Q( X ) |
|
Q ( X ) q |
(2.14) |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
1 |
|
где Q j ( X ) e j ( X ) |
|
, j |
[1, M ]; |
H 0 j - заданная "эталонная" функция; |
|
||
j |
H 0 j f j |
|
|||||
q 1 - целое положительное число.
94

Когда требования ЧТЗ заданы в виде коридоров допусков, то в [2] предложено вместо обобщенного критерия (2.14)использовать критерий вида
|
|
|
|
Qj ( X ) s |
1s |
|
|||
Q( X ) |
|
Qmax |
|
|
|
, |
(2.15) |
||
j J Qmax |
|||||||||
|
|
|
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
s qsign(Qmax ) , |
|
|
||||
|
|
|
|
|
|||||
J |
{ j |
Q j ( X |
0)}, при Qmax |
0 |
|
||||
1 : M , при Qmax 0 |
|
|
|||||||
|
|
|
|||||||
|
|
Qmax |
max Q j ( X ) |
|
|
||||
|
|
|
|
[1,M ] |
|
|
|||
При положительном максимальном отклонении |
Qmax обобщенный критерий (2.15) |
||||||||
формируется из положительных функций-отклонений и наоборот. |
|
||||||||
Функции f j (X ) , Q j ( X ) , |
|
j [1: M ] могут быть как линейными, так и нелинейными |
|||||||
функциями параметров X. Исходя из |
условий работоспособности, |
решение ЗВО может |
|||||||
считаться удовлетворительным, если все локальные критерии Q j ( X ) принимают отрицательные значения. Таким образом, задача векторной оптимизации УЦОС сведена к задаче скалярной оптимизации. В качестве целевой функции последней задачи выступает обобщенный критерий оптимальности, формируемый на основе совокупности локальных
критериев Ошибка! Источник ссылки не найден. или функций f j (X ) , j |
[1: M ] . Задача |
||||||
скалярной оптимизации имеет в рассматриваемом случае вид |
|
||||||
|
|
|
min Q( X ). |
|
|||
|
|
|
X |
D |
|
|
|
Мультипликативный и аддитивный обобщенные критерии соответственно |
|||||||
определяются выражениями |
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
iQi ( X ) |
|
||
|
Q( X ) |
|
i 1 |
|
|
|
(2.146) |
|
|
m2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
k Qk ( X ) |
|
||
|
|
|
k m1 |
1 |
|
|
|
|
m1 |
|
|
m2 |
|
|
|
Q( X ) |
|
iQi ( X ) |
k Qk ( X ), |
(2.17) |
|||
|
i 1 |
|
|
k m1 |
1 |
|
|
где первые m1 функций должны уменьшаться, а остальные m2-m1 - увеличиваться.
Недостатками критериев вида (2.16), (2.17) являются [7, 10, 30, 48]: неограниченная возможность компенсации уменьшения качества по одному локальному критерию
95

увеличением качества по другому (другим), что в ряде случаев маскирует внутренние технические противоречия оптимизируемого УЦОС.
Данные недостатки устранимы при использовании максиминного обобщенного критерия. В максиминном критерии, предложенном в [54], вводятся запасы работоспособности, представляющие собой относительные (безразмерные) оценки выполнения каждого из условий работоспособности
Qj |
j min |
f j ( X ) Z1 j |
1, |
Z |
2 j |
f j |
( X ) |
1 , |
(2.18) |
|
|
|
|
|
|||||
j |
|
|
j |
|
|||||
|
|
|
|
|
|
|
|
||
где j - оценка рассеяния значений j-той функции. |
|
|
|
|
|
|
|||
Величина j задается равной допуску или статистическому разбросу |
f j (X ) . Если эти |
||||||||
величины неизвестны, ими надо задаваться исходя либо из предварительных расчетов, либо из опыта. Например, если путем расчетов или опытным путем установлено, что функция
f j (X ) распределена по нормальному закону с дисперсией |
j, |
то полагая, что в процессе |
||
оптимизации дисперсия |
j меняется мало, можно считать j=3 |
j. |
|
|
При известных оценках рассеяния задачу векторной оптимизации можно поставить и |
||||
решить как максиминную |
|
|
|
|
|
max min Qj ( X ) |
|
(2.19) |
|
|
X D j [1:M ] |
|
|
|
или минимаксную |
|
|
|
|
|
min max |
Q j ( X ) |
|
(2.20) |
|
X D j [1:M ] |
|
|
|
При отсутствии |
оценок рассеяния |
j, j [1: M ] задача |
(2.20) сводится к задаче |
|
Ошибка! Источник ссылки не найден..
Критерий (2.18) также, как и критерий Ошибка! Источник ссылки не найден., не является гладким, что существенно усложняет задачу оптимизации и требует применения специальных алгоритмов [54, 55]. В ряде случаев применяется подход, основанный на процедуре сглаживания критерия (2.20) с последующим обращением к методам гладкой оптимизации [3, 5, 7, 11, 28, 48].
Так как
arg min Qj |
arg max e |
Q j |
|
||
j |
j |
|
то задача (2.20) эквивалентна задаче
max e Q j min . |
(2.151) |
j |
|
96
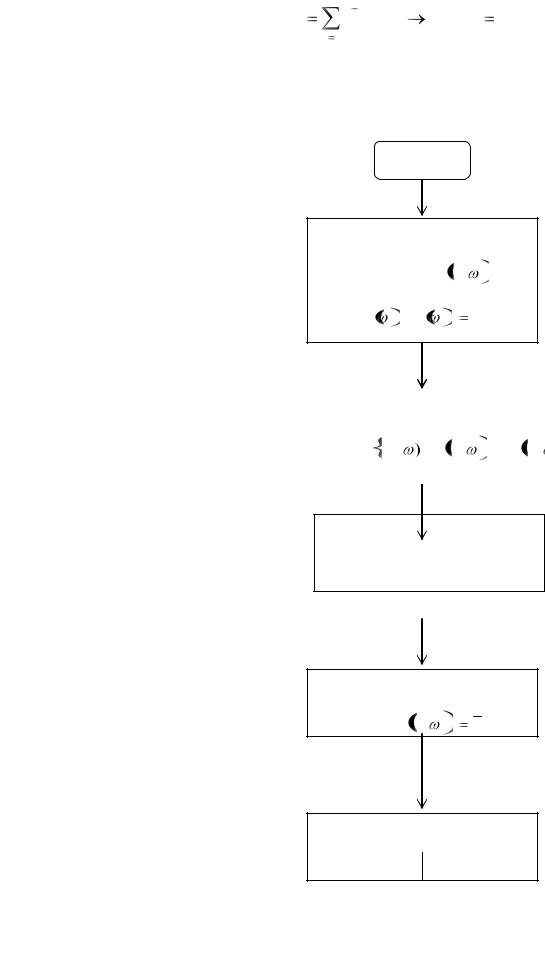
Здесь к (2.21) применима среднестепенная свертка Ошибка! Источник ссылки не найден.. В результате приходим к следующему обобщенному критерию оптимальности:
M |
|
qQ j ( X ) |
|
|
|
Q( X ) |
e |
min (q 1,2, ). |
(2.22) |
||
|
|||||
j |
1 |
|
X |
|
|
|
|
|
На
Расчет частотных (временных)
|
|
|
|
характеристик H i |
X , |
|
и их |
граничных значений |
|||
|
|
|
|
H Hi , H Bi |
,i |
1, P |
|
Формирование |
|
вектора |
функций отклонения (ЛКО) |
||
|
|
|
e1(X, |
, e2 X , |
,..., eP X |
|
|
|
Выбор номера обобщенного критерия оптимальности из базового набора
Нормирование
функций
ei X , , i 1, P
Расчет численного значения обобщенного
критерия
97

Ко
Рис 2.1 Схема алгоритма расчета обобщенных критериев оптимальности УЦОС
В результате, при решении задач векторной оптимизации УЦОС, когда требования ЧТЗ к ЧХ заданы либо в виде односторонних, либо в виде двусторонних неравенств, в
качестве обобщенных критериев оптимальности целесообразно использовать целевые функции вида Ошибка! Источник ссылки не найден., (2.14) – (2.20) и (2.22). Алгоритм формирования базового набора обобщенных критериев оптимальности УЦОС приведен на рис.2.1.
Рассмотренные выше целевые функции вошли в библиотеку целевых функций подсистемы оптимального проектирования УЦОС [62]. Базовый набор целевых функций,
введенный в состав библиотеки алгоритмов подсистемы, позволяет сформировать различные требования к проектируемому устройству, и обеспечивает решение широкого круга задач оптимального проектирования УЦОС в различной постановке.
2.2 Алгоритмы экономичных вычислений частотных характеристик
цифровых фильтров
Оптимальное проектирование УЦОС крайне затруднено даже с применением
высокопроизводительных ПЭВМ и инженерных рабочих станциях (ИРС). Так как:
-в обобщенные критерии входит большое количество характеристик УЦОС, расчет которых требует значительных машинных и временных ресурсов;
-на каждом оптимизационном шаге используется многократный расчет всего устройства в целом, при этом основное время и ресурсы занимает расчет передаточных функций цифровых фильтров, входящих в состав УЦОС.
Рассмотрим основные приемы сокращения вычислительных затрат при решении задач
оптимизации УЦОС, когда в их структуре имеется либо нерекурсивный , либо рекурсивный цифровые фильтры (НЦФ, РЦФ) [15, 33, 72].
Прежде всего рассмотрим алгоритм расчета частотных характеристик (ЧХ) НЦФ.
Практически реализуемую ЧХ НЦФ можно записать в виде [72]
H (k) A(k)e j (k ) R(k) Y (k ) , |
(2.23) |
где k [1: M ] , M - число точек дискретизации на оси частот. Тогда процедуру расчета ЧХ НЦФ условно можно представить следующей схемой:
98
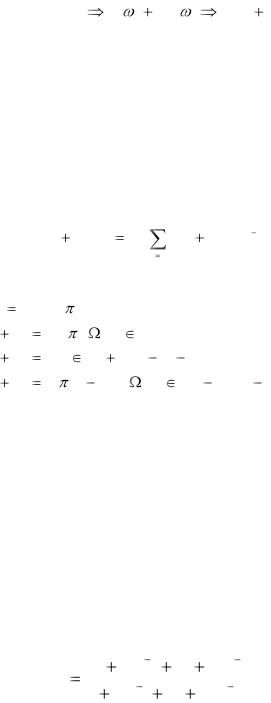
h(t) R( ) jY( |
) |
R(k) jY(k) . |
(2.24) |
Расчет ЧХ НЦФ непосредственно |
по |
формуле (2.24) потребует |
больших затрат |
машинного времени. Для снижения этих затрат целесообразно воспользоваться дискретным быстрым преобразованием Фурье (БПФ). Если воспользоваться стандартной процедурой БПФ, то время на подготовку данных для решения задачи расчета ЧХ НЦФ и ресурсы памяти ПЭВМ будут весьма значительными. Поэтому целесообразно воспользоваться приближенно быстрым дискретным преобразованием Фурье [72]. Тогда формулу (2.24)
можно записать следующим образом:
|
|
|
|
1 N |
|
|
|
kn , |
(2.25) |
|
|
|
R(k) |
jY (k) |
|
( p |
n |
jq |
)W |
||
|
|
|
||||||||
|
|
|
|
M n 0 |
n |
|
M |
|
||
|
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
WM |
exp( j2 |
/ M ); |
|
|
|
|
|
|
|
|
pn |
qn |
h(n |
/ ), n |
[0, N ] |
|
|
|
|
|
|
pn |
qn |
0, n [N 1, M N 1] |
|
|
|
|
||||
pn |
qn |
h( |
(n M ) / |
), n [M |
N, M |
1], |
|
|||
Здесь N - положительное целое число, удовлетворяющее условию 2N < M.
С применением формулы (2.25) задача минимизации обобщенных критериев оптимальности из базового набора для НЦФ может быть решена одним из методов 0-го порядка, то есть методом минимизации с использованием только значений обобщенных критериев оптимальности и без вычисления их производных [3, 5, 7, 9, 12, 18, 34, 48, 66, 74, 78].
Для расчета ЧХ РЦФ, целесообразно воспользоваться следующим приемом, в основе которого лежит схема Горнера [30]. С этой целью представим передаточную функцию РЦФ в следующем виде:
|
a |
a z 1 |
a |
n |
z n |
|
|
H (z) |
0 |
1 |
|
|
. |
(2.26) |
|
1 |
b z 1 |
b z m |
|||||
|
|
1 |
m |
|
|
|
|
Используем для расчета АЧХ и ФЧХ схему Горнера, |
согласно которой значение |
||||||
полинома Р(a,z)=a0+a1z-1+…+anz-n при z=zk определяется по следующим рекуррентным соотношениям:
cn=an |
|
ci=ai+ci+1zk, i=n-1,…,1,0, |
(2.27) |
P(a,z)=c0.
Так как z=e-jT, где - значение частоты, а T - период дискретизации, то соотношение (2.27) для zk=e-jkT имеет вид
Rn=an
99

Ri=bi+Ri+1cos k T )-Ii+1sin k T ),
Ii=-Ri+1sin k T )+Ii+1cos k T ), i=n-1,…,1,0,
A(e-jkT)=R0 k T )+jI0 k T ).
По аналогии вычисляются значения полинома знаменателя
B(e-jkT)=K0 k T )+jL0 k T ).
Тогда значение АЧХ на частоте k вычисляется по формуле
H (e j kT ) |
|
|
R 2 |
( |
|
T ) |
I 2 |
( |
|
T ) |
|
|
|
|
|
|
|
|
|||||||||
|
0 |
|
k |
|
0 |
|
k |
|
|
, |
|||
|
|
K 2 |
( |
k |
T ) |
L2 |
( |
k |
T ) |
||||
|
|
|
|
|
|||||||||
|
0 |
|
|
0 |
|
|
|
|
|||||
а значение ФЧХ - по формуле:
( |
|
T ) arctg |
I0 |
arctg |
L0 |
. |
k |
|
|
||||
|
|
R0 |
|
K0 |
||
|
|
|
|
|||
Здесь для расчета АЧХ требуется выполнить только 8n операций умножения, где n -
порядок передаточной функции, и только два вычисления функций sin k T ) и cos k T )
независимо от n. Число операций умножения и вычисления этих функций непосредственно по соотношению Ошибка! Источник ссылки не найден. равно соответственно 4n и 2n. При реализации на ПЭВМ вычислений sin k T ) или cos k T ) требуется обращение к соответствующим подпрограммам, в которых обычно используется 3...4 члена разложения функции в ряд Тейлора, т. е. требуется в среднем восемь операций умножения.
Следовательно, при вычислении АЧХ звена цифрового фильтра второго порядка схема Горнера дает выигрыш в восемь операций умножения для каждого значения частоты. При увеличении порядка фильтра этот выигрыш существенно возрастает.
Рассмотрим еще один алгоритм приближенного расчета обобщенных критериев,
используемый в данной работе. Его применение тем более целесообразно, чем сложнее математическая модель УЦОС, расчет которой необходим для вычисления значения целевой
функции (обобщенного критерия). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Особенность предлагаемого алгоритма заключается в том, что каждая из функций |
|||||||||||||||||||||||
Qi ( X |
p) |
заменяется параболой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
Q |
pi |
( X |
p) |
|
a |
i |
b |
c |
i |
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|||
|
|
|
Коэффициенты ai , |
bi , ci |
определяются как решение системы линейных уравнений, |
|||||||||||||||||||||
полученной |
из |
|
условия |
|
минимума |
|
|
|
суммы |
|
|
квадратов |
отклонений параболы |
|||||||||||||
Q |
pi |
( X |
p) |
a |
i |
b |
c |
i |
2 |
от функции Q |
i |
в точках |
X |
0 |
, X |
1 |
, |
X |
2 |
на луче p . Таким образом, |
||||||
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
если функция Qi ( X |
p) |
достаточно хорошо аппроксимируется параболами, то и функция |
||||||||||||||||||||||||
100

Q(X  p) успешно аппроксимируется функцией Qp ( X
p) успешно аппроксимируется функцией Qp ( X 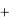 p) . При этом функция Q(X
p) . При этом функция Q(X  p)
p)
может и не обладать свойствами квадратичности.
2.3 Построение алгоритмов вычисления производных обобщенных
критериев оптимальности УЦОС
При решении задач оптимального проектирования УЦОС с использованием обобщенных критериев типа (2.14), (2.15) и (2.22) возникает необходимость расчета производных этих критериев. Для обобщенных критериев, заданных аналитически, можно воспользоваться аналитическими методами вычисления производных. Однако на практике такой подход имеет ограниченное применение, так как в конкретных задачах реальные обобщенные критерии имеют достаточно сложную структуру, не позволяющую воспользоваться аналитическим дифференцированием. Поэтому наряду с аналитическими на практике применяются также полуаналитические и численные методы. Следовательно, в
коллектив конкурирующих алгоритмов расчета производных обобщенных критериев типа
(2.14), (2.15) и (2.22) целесообразно включить алгоритмы, основанные на использовании аналитических, полуаналитических и численных методов.
Достоинства аналитических методов широко известны, однако область их применения достаточно ограничена. В основном они применяются при оптимальном проектировании широкополосных селективных УЦОС невысокого порядка.
Полуаналитические методы занимают промежуточное положение между аналитическими и численными методами построения производных. Эти методы основаны на использовании специальной структуры оптимизируемых обобщенных критериев и в этом смысле оказываются менее универсальными, чем численные методы. Область их применения занимает промежуточное положение между узкополосными и широкополосными селективными УЦОС. В силу универсальности и относительной простоты реализации численные методы расчета производных используются при решении задач оптимального проектирования узкополосных селективных УЦОС большой размерности. Таким образом,
основным критерием адаптации при проблемно – адаптивной организации подсистемы расчета производных обобщенных критериев является размерность вектора варьируемых параметров.
Общая схема алгоритмов расчета производных обобщенных критериев оптимальности УЦОС и их производных приведена на рис. 2.2.
101
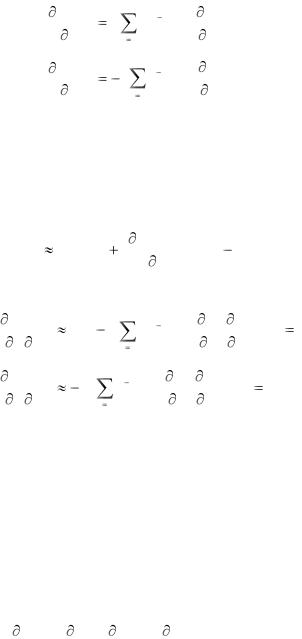
Рассмотрим обобщенные критерии вида Ошибка! Источник ссылки не найден. и
(2.22), как наиболее характерные для задач оптимального проектирования УЦОС. Имеем следующие выражения для составляющих вектора градиента:
|
|
|
Q( X ) |
q |
Q q |
1 |
( X ) |
|
Ql ; |
|
|
|
(2.28) |
|||||||||
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|||||
|
|
|
l |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Q( X ) |
q |
e qQl ( X ) |
|
Ql |
, |
|
|
(2.29) |
|||||||||||
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
l 1 |
|
|
|
|
|
|
|
xi |
|
|
|
|
||||
где Ql - локальные критерии УЦОС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вторые производные можно получить путем линеаризации функций |
Ql вблизи |
|||||||||||||||||||||
текущей точки X * : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Q ( X * ) |
|
|
Q ( X * ) |
|
|
|
|
|
|
|
X * ). |
|
|||||||
Q (X ) |
( |
|
l |
|
|
|
, |
|
|
X |
(2.30) |
|||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
l |
l |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Используя (2.30), получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2Q( X ) |
|
|
|
M |
2 |
|
|
|
|
|
Q |
Q |
|
|
|||||||
|
|
|
q(q |
1) |
|
( X ) |
|
l |
l |
, |
q 2,3, ; |
(2.161) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
xi xk |
|
|
|
|
|
l |
|
|
|
|
|
|
|
xi |
xk |
|
|
||||
|
|
|
|
l |
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
2Q( X ) |
|
|
M |
qQl ( X ) |
|
|
Q |
|
|
|
|
Q |
|
|
|
|
|||||
|
|
|
q2 |
e |
|
|
l |
|
l |
, |
q |
1,3, |
(2.32) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
xi xk |
|
|
l |
1 |
|
|
|
|
xi |
|
|
|
|
xk |
|
|
|
|
|||
Следовательно, вычисление |
вторых |
|
|
производных |
оптимизируемого |
обобщенного |
||||||||||||||||
критерия может быть сведено к вычислению первых производных функций Ql . Таким образом, при оптимизации обобщенных критериев оптимальности УЦОС достаточно остро стоит проблема расчета их производных.
Рассмотрим вывод формулы вектора градиента для обобщенного критерия типа (2.14)
в случае, когда решается задача проектирования НЦФ и РЦФ. Для других случаев эти формулы выводятся аналогично. Компонентами вектора градиента, которые должны быть определены, являются Q( X ) / pn и Q( X ) / qn .
Принимая во внимание, что для НЦФ имеет место соотношение (2.23) и
продифференцировав в частных производных формулу Ошибка! Источник ссылки не найден. по pn и qn, а также произведя требуемые алгебраические преобразования, получим:
102
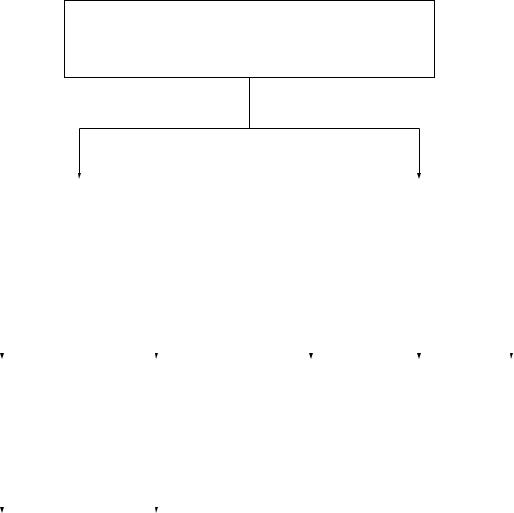
Методы вычисления обобщенных критериев и их производных
Обобщенные критерии |
|
|
Производные обобщенных |
|
||
|
|
критериев |
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нерекурсивные |
|
Рекурсивные |
|
|
|
Полуаналити- |
|
Алгоритми- |
||
|
|
Аналитически |
|
ческим |
|
|||||
структуры |
|
структуры |
|
|
|
чески |
||||
|
|
|
|
способом |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На основе БПФ |
|
На основе |
|
схемы Горнера |
|
|
|
|
|
|
|
Рис. 2.2. Общая схема алгоритма реализации методов вычисления обобщенных критериев и их производных
103
