Методическое пособие 484

Методы второго класса, среди которых большее внимание уделяется применению множителей Лагранжа, обычно применяют при наличии нелинейных ограничений. Оценки множителей Лагранжа [28, 93] вычисляются в большинстве современных алгоритмов.

Изначально для решения задачи НЛП с нелинейными ограничениями использовался метод штрафных функций. Позднее был разработан метод барьерных функций с включением в него процедуры экстраполяции. Этот метод, известный под названием SIMT, успешно применялся для решения практических задач [28]. Однако и он имеет ряд недостатков,

вызванных его плохой обусловленностью. В последующих работах этого направления были разработаны новые штрафные функции, свободные от этого недостатка, а также не имеющие особых точек и позволяющие быстро и с минимальным числом вычислений целевой функции определить ее минимум [28]. Это позволило без модификаций применить процедуру безусловной минимизации для решения ряда задач НЛП за приемлемое время.

Эффективность этой процедуры существенно влияет на эффективность алгоритма оптимизации.

В работе [18] при сравнении этих двух подходов отмечалось, что второй "считается в настоящее время неэффективным с точки зрения объема вычислений". В работе [11] на основании большого опыта решения различных задач оптимизации (в том числе и вида (2.12)

утверждается, что алгоритмы, использующие второй подход, "крайне ненадежны, сходятся очень медленно и критерий прекращения счета по стабилизации результата с заданным числом знаков создает иллюзию успешного решения задачи".

Наибольшее развитие среди методов первой группы получили квазиньютоновские методы (КНМ) и градиентные методы сопряженных направлений, в которых вычисляются значения целевой функции и ее градиента. При этом основная итерационная формула имеет вид

где X (k 1) , X (k ) - точки в пространстве варьируемых параметров, являющиеся приближением

оптимального решения X * ; G(k ) - вектор спуска (направления поиска); k - шаг вдоль

направления G(k ) .

Все методы безусловной минимизации отличаются друг от друга способом

определения вектора G(k ) и шага k . В КНМ направление поиска находится по формуле:

116

где Q( X (k ) ) - градиент обобщенного критерия; H (k ) - матрица, аппроксимирующая

обратную матрицу Гессе целевой функции [3, 18].

Основные разработки в КНМ были связаны с поисками наиболее точных формул

получившее название квазиньютоновского условия [93]. Существуют различные способы удовлетворения этого условия. При этом основная задача состоит в построении достаточно простой формулы коррекции, требующей небольшого объема вычислений и вместе с тем эффективной.

Наиболее простой является формула коррекции единичного ранга (иногда ее

117

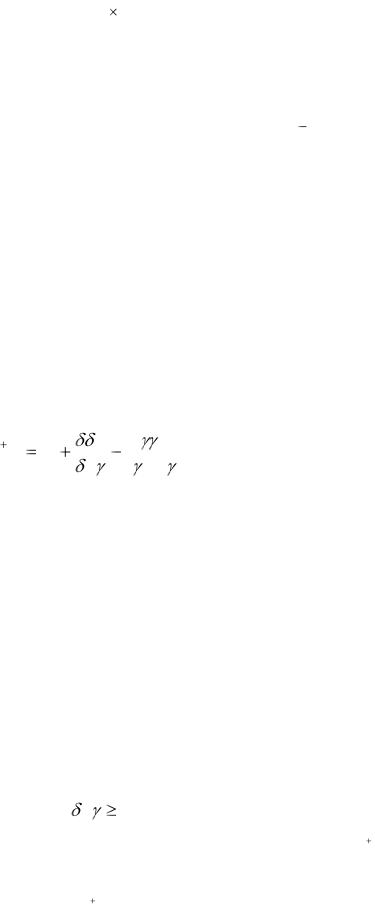
где второе слагаемое представляет собой n n матрицу единичного ранга. Здесь и в дальнейшем для сокращения обозначений индекс k в правой части формулы коррекции будет опущен. Примечательной особенностью этой формулы является то, что для нее не требуется производить точный линейный поиск. Более того, для сходимости алгоритма не обязательно, чтобы направление поиска определялось по формуле G (k ) H (k ) g (k ) . Однако формула (3.13) имеет два существенных недостатка [93]:

-она не гарантирует положительную определенность матрицы H (k ) даже для квадратичных функций;

-знаменатель во втором слагаемом может стать близким или равным нулю, что приведет к срыву процесса минимизации, и поэтому практический алгоритм должен включать в себя дополнительные приемы, позволяющие преодолеть эти недостатки, что в общем нельзя признать наилучшим выходом.

Другой формулой коррекции, получившей широкое распространение в прошлом при решении различных задач оптимизации, является формула Давидона-Флетчера-Пауэлла

(ДФП) [93]:

В первых программных реализациях метода ДФП применялся очень точный линейный поиск, что позволяло получить хорошие результаты, но требовало большого числа вычислений целевой функции. Дальнейшие исследования формулы (3.14) при менее точном линейном поиске показали, что в этом случае она уступает другим формулам коррекции [18, 93]. Поэтому в настоящее время метод ДФП признан не самым эффективным методом из класса КНМ [93].

Не смотря на то, что все матрицы H (k ) в этом методе должны быть положительно определены, из-за ошибок округления в практических расчетах на ЭВМ положительная определенность матрицы может быть потеряна. Это приведет к шагу в направлении возрастания целевой функции и преждевременному окончанию работы алгоритма. Во избежании этого производится проверка условия

матрица H (k ) также положительно определена. В случае невыполнения условия (3.15) на каком-либо шаге минимизации, матрица H (k 1) заменяется на единичную.

118

Кроме того в методе ДФП, матрица H (k ) может стать неопределенной или почти неопределенной. Это может произойти в том случае, если величина знаменателя T H будет

близка или равна нулю, что вызовет переполнение разрядной сетки ЭВМ или очень большой шаг в направлении G(k ) . Во избежании этого в ряде исследований предлагалось заменить

матрицу H (k 1) на единичную H 2 через каждые k итераций, что позволяет обеспечить

сходимость к стационарной точке. Но скорость сходимости метода при этом существенно замедляется.

При коррекции матрицы H (k ) ошибки округления часто приводят к тому, что направление поиска G(k ) будет почти перпендикулярно к градиенту целевой функции, т.е.

будет сильно отличаться от направления ее наискорейшего убывания. Поэтому, если выполняется условие

следует заменить на единичную или на другую, положительно определенную матрицу.

Улучшенными вычислительными возможностями обладает метод Бройдена-

Его основным преимуществом является малая критичность к точности линейного поиска, что делает его весьма эффективным с точки зрения объема вычислений. Формула коррекции (3.15) сохраняет все важные теоретические свойства КНМ. Кроме того,

теоретически доказана глобальная сходимость метода БФГШ с приближенным линейным

поиском.

Соотношения (3.13) и (3.15) в своей линейной комбинации образуют однопараметрическое семейство формул коррекции второго ранга, получившее название

семейства Бройдена [18, 48, 93]:

Это семейство включает в себя и формулу ДФП (Ф=0), и формулу БФГШ (Ф=1), и ряд других формул. Важным является то, что многие свойства формул коррекции ДФП и БФГШ

119

являются общими для всего семейства формул (3.17) В несколько преобразованном виде с учетом выражений (3.14), (3.15) формулу (3.18) можно представить так:

где

Анализ собственных чисел матрицы HФk 1 показывает, что ее положительная Ф

определенность будет обеспечена, если параметр будет удовлетворять условию [3, 12, 18, 93]:

выпуклым классом формул, принадлежащих семейству (3.19). Для выбора значения параметра Ф Флетчер предложил выполнять проверку следующего условия [93]:

противном случае Ф 0 и применяется формула ДФП. Этот метод в сочетании с процедурой приближенного линейного поиска хорошо зарекомендовал себя при решении ряда тестовых задач и в настоящее время широко используется во многих программах оптимизации.

Впервых программах, использовавших целевую функцию вида (2.14),

предпринимались попытки решать задачу оптимизации как общую задачу НЛП с последовательным увеличением q от итерации к итерации [28]. Это приводило к потере точности и устойчивости вычислительного процесса вследствие оперирования с очень большими и очень малыми числами (т.е. задача была плохо обусловлена). Отметим, что целевая функция (2.15) свободна от этого недостатка и входящий в нее показатель степени принимает небольшие положительные целочисленные значения. Поэтому на практике при решении задачи оптимизации УЦОС чаще применяется целевая функция (2.15).

Решение задач минимизации обобщенных критериев оптимальности рассмотренными методами может быть представлено следующим алгоритмом:

120

min Q( X (k ) k G(k ) ).

k

Шаг 4. Установить k k 1; если не выполнено условие останова, то перейти к шагу

2.

Повышение эффективности решения поставленной задачи означает уменьшение общего количества определений целевой функции на шагах 2 и 3. Рассмотрим вопросы

уменьшения количества определений целевой функции на шаге 3.

В настоящей работе использован алгоритм одномерной минимизации, построенный на приближенном вычислении целевой функции, изложенном в п. 2.2. Его применение тем более целесообразно, чем сложнее математическая модель УЦОС, расчет которой необходим для вычисления значения целевой функции (обобщенного критерия). Здесь минимизация

целевой функции сведена к многошаговой процедуре, на каждом l -том шаге которой методом дихотомии [31] минимизируется не функция Q , а ее приближенное значение Qp и в точке минимума приближенной функции рассчитывается относительная погрешность Q

расчета функции. Особенность используемого алгоритма заключается в том, что каждая из

следующему шагу.

Кроме того в реализованном алгоритме направление движения к оптимуму на шаге 2

определяется по формуле

Приведенная формула реализует метод сопряженных градиентов с улучшенной обусловленностью, что заметно повышает эффективность реализованного алгоритма при решении задач оптимизации типа (3.1) с целевыми функциями (2.15) и (2.22).

121

Начало

K=0

Определение направления поиска

Одномерный поиск

K=K+1

Конец

Рис. 3.2 Структурная схема алгоритма минимизации обобщенных критериев

123