Методическое пособие 484

отброшены все заведомо худшие в смысле векторной оптимизации варианты и предельно

сужена область поиска.

84

85

1.3 Обзор методов решения задач векторной оптимизации

Решение ЗВО УЦОС Ошибка! Источник ссылки не найден. осуществляется в два этапа. Первый этап заключается в определении вариантов построения устройств,

оптимальных по Парето или в определении области компромиссов. На втором этапе определяется единственный вариант построения устройства на основе некоторого принципа оптимальности. При этом для принятия решения о выборе привлекается дополнительная информация, которой, как правило, владеет только опытный проектировщик (эксперт).

Формализация задачи второго этапа чрезвычайно затруднена и на практике очень часто не удается построить автоматический алгоритм отбора. В связи с этим возникает необходимость в организации человеко-машинных процедур (диалога) принятия решения о выборе.

Методы определения множества Парето по типу требуемой априорной информации и способу получения решения можно условно разбить на две группы [11] (см. рис. 1.6) :

методы, основанные на сведении задач векторной оптимизации к задачам скалярной оптимизации [1, 7 - 11, 13, 14, 12, 16, 19 - 20, 24 - 25, 27, 31, 43, 67 - 68, 73, 94, 96, 98],

ставшие уже классическими, и методы поиска непосредственно на множестве допустимых решений [85], появившиеся сравнительно недавно и используемые, как правило, в составе человеко-машинных процедур. В составе человеко-машинных процедур используются и методы первой группы, что способствует сокращению вычислительных затрат и повышает качество решения.

Скаляризация векторного критерия в методах первой группы может быть осуществлено различными способами. Выделение главного критерия [1, 19 – 20, 47 - 48]

является простейшим из таких методов достижения множества Парето, который можно считать частным случаем метода последовательных уступок [19]. Эти методы применимы в том случае, когда один из ЛКО обладает исключительной важностью. В зарубежной литературе это направление получило наименование задачи оптимизации k-го критерия с l-

ограничениями [104]

Методы решения задачи (1.25) - (1.26) хорошо разработаны и продолжают развиваться [3 - 5, 7 – 9, 12 - 13, 16, 18, 26 - 28, 30, 32, 34, 48 - 50, 53 – 55, 64, 66 - 67, 69 - 71, 74, 78, 92 – 93, 99, 100 - 107]. Тем не менее, при

86

Указанные недостатки сохраняются, если рассматривать функцию Лагранжа,

построенную на основе задачи (1.25), (1.26). Метод последовательных уступок обеспечивает выравнивание локальных критериев за счет их последовательной замены при формировании целевой функции. Однако этот путь сложен и не экономичен по затратам времени ПЭВМ,

так как необходимо решать последовательность задач (1.25), (1.26).

Широкое распространение среди методов первой группы получил также метод свертки компонент векторного критерия Qk , k [1,M], который предполагает построение некоторого обобщенного (агрегированного) критерия на множестве значений векторного критерия. Обобщенный критерий должен правильно отражать значимость локальных критериев и не нарушать отношений предпочтения на множестве решений. После того как такой обобщенный критерий построен, решается задача скалярной оптимизации обобщенного критерия. Очевидно, что если обобщенный критерий не нарушает отношения предпочтения, то такой вектор Q принадлежит множеству парето-оптимальных решений задачи векторной оптимизации.

Свертывание векторного критерия в скалярный в методах первой группы может быть осуществлено различными способами [1, 7 – 9, 11, 13, 17, 19, 25, 27, 31, 48, 77], однако наиболее пригодными для целей проектирования УЦОС являются среднестепенная норма [1, 11, 50, 86, 90, 96]

i1

иминимаксная (чебышевская) норма [21, 48, 67, 71, 79]

Для критерия (1.27) 1 р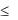 . При р=1 обобщенный критерий (1.27) превращается в линейную комбинацию локальных критериев, а при р=0 - в обобщенный минимаксный критерий [79] типа (1.28). Применяя минимаксный критерий, можно получить гарантированные результаты.

Однако применение среднестепенного критерия (1.27) обладает тем преимуществом,

что в этом случае можно использовать обычные методы оптимизации. За счет увеличения показателя р получают результаты близкие к минимаксному решению. Но с ростом р рельеф результирующего обобщенного критерия Q(X ) будет иметь глубокие «овраги», что замедляет сходимость многих методов оптимизации и часто приводит к преждевременным остановам [11, 13, 96].

88

Обобщенные критерии (1.27) и (1.28) имеют свои достоинства и недостатки.

Функционал (1.27) при р=2 достаточно прост и обладает свойством «гладкости». Основными недостатками рассматриваемой модели векторной оптимизации являются: неограниченная возможность компенсации уменьшения качества по одному критерию увеличением качества по другому (другим); разные альтернативы соответствуют одним и тем же значениям обобщенного критерия (1.27). Для устранения указанных недостатков приходится вводить дополнительные условия и ограничения на критерии, дающие неприемлемые результаты,

сокращая таким образом область допустимых решений (методы ограничений и их различные модификации [96]). Кроме того, следует отметить, что выбор априори весовых коэффициентов i в свертке представляет собой нетривиальную задачу.

Многие недостатки обобщенного критерия (1.27) при р=1 и р=2 устранены в минимаксном критерии (1.28). Достоинством данной модели векторной оптимизации является отсутствие необходимости в априорной информации об отношениях предпочтения на множестве ЛКО, кроме того, этот метод позволяет получить наилучшее решение при наихудшем сочетании весовых коэффициентов («гарантированный результат»), и может быть использован для предварительной оценки оптимального компромиссного решения.

Дополнительно следует отметить, что введение в минимаксную модель весовых коэффициентов позволяет получить любую точку множества Парето, тогда как свертка позволяет получать точки множества Парето только на выпуклой границе этого множества

[11]. Однако минимаксный критерий не сохраняет характеристики «гладкости» функции,

платой за что является существенное увеличение сложности методов решения.

Достаточно простой и надежный способ решения ЗВО заключается в использовании гладких среднестепенных аппроксимаций минимаксного критерия (1.28). Функционал (1.27)

при р>2 совмещает в себе достоинства функционала (1.27) при р=1 и р=2. Являясь гладким подобно (1.27) при р=2, он не допускает значительных отклонений точности минимизации отдельных локальных критериев. Существенным недостатком обобщенного критерия (1.27)

при р>2 является то, что при его использовании возникает переполнение разрядной сетки ПЭВМ при возведении первоначально больших значений локальных критериев в высокую степень р, а также «овражный» характер функционала (1.27) при увеличении степени р.

Достоинством методов первой группы является возможность использования для решения задачи обычных методов и алгоритмов скалярной оптимизации, математический аппарат которых в настоящее время развит достаточно глубоко [3 – 5, 7, 9, 11 – 12, 16, 18, 22 - 23, 25 - 26, 32 - 33, 34 - 35, 48, 50, 53, 55]. Кроме того, применение методов данной группы

89

обеспечивает, как правило, достаточно высокую точность поиска решения. Недостатком рассмотренных методов являются необходимость в априорной информации об отношениях предпочтения проектировщика на множестве локальных критериев, которая часто либо отсутствует, либо отличается известной долей субъективизма, а также достаточно высокие затраты на поиск.

Предполагающие непосредственный поиск на множестве допустимых решений,

методы второй группы являются в большинстве своем эвристическими и переборными [1]. В

частности, в технических приложениях наибольшее распространение получили методы,

основанные на равномерном покрытии множества допустимых решений некоторыми сетками, то есть методы, сводящиеся по сути своей к случайному (квазислучайному) поиску.

При этом наибольшее распространение получил квазислучайный поиск на основе ЛП -

последовательностей (метод Соболя – Статникова) [83 - 85]. Для обработки полученных результатов и выбора оптимального решения в методе ЛП -поиска реализован алгоритм построения наглядных рабочих таблиц, позволяющий проектировщику выбирать подходящие парето-оптимальные решения [85].

Важным достоинством метода ЛП -поиска является отсутствие в необходимости априорной информации об отношениях предпочтения на множестве ЛКО, простота реализации, возможность применения как для решения задач безусловной оптимизации, так и для решения задач оптимизации с ограничениями. Кроме того, методы на основе случайного (квазислучайного) поиска в ходе работы позволяют получить дополнительную информацию о решаемой задаче, например, оценки минимальных и максимальных значений ЛКО, информацию о взаимном влиянии ЛКО, а также ориентировочные значения весовых коэффициентов в (1.27) при р=1 [85]. Еще одним важным достоинством является то, что методы подобного рода позволяют получить сразу несколько альтернативных решений,

тогда как методы первой группы в каждый момент времени дают только одно решение.

Существенным недостатком метода ЛП -поиска является сравнительно низкая точность поиска решения. При попытке же увеличения точности за счет повышения числа пробных точек резко увеличиваются затраты на поиск при сомнительном повышении качества решения.

Ко второй группе методов можно отнести и появившееся сравнительно недавно векторно-релаксационные алгоритмы [76 - 77], которые обладают чертами релаксационных алгоритмов скалярной оптимизации и позволяют осуществить целенаправленный перебор точек множества Парето, исключая при этом заведомо неэффективные точки. Большим

90

достоинством данных алгоритмов является возможность целенаправленного перехода от одной точки множества Парето к другой и отсутствие в необходимости дополнительной априорной информации, а также относительно высокая точность получаемого решения.

Недостатком являются высокие затраты на поиск, особенно при старте из «неудачной» начальной точки.

Задачи оптимального проектирования УЦОС как известно, формулируются как задачи выбора одной наилучшей альтернативы. Последнее предполагает существование и использование при формальном анализе альтернатив обобщенного (интегрального,

агрегированного) критерия оптимальности, который определяет компромисс между степенями достижения целей проектирования, оцениваемых значениями локальных критериев. Обоснованность выбора какой-либо альтернативы как наилучшей определяется тем, что в достаточно большом числе случаев целевые установки (мотивы) выбора наилучшей альтернативы достаточно адекватно отражены в обобщенном критерии. Поэтому построение и оптимизация таких адекватных реальности обобщенных критериев в каждой конкретной задаче проектирования имеет первостепенное значение.

Оптимизация обобщенных критериев УЦОС имеют свои характерные особенности,

приводящие на практике к существенным трудностям, вызванным следующими причинами

[41 - 42, 62]:

1.Одним и тем же значения обобщенных критериев оптимальности могут соответствовать разные альтернативы.

2.Зачастую задачи оптимизации УЦОС характеризуются большим количеством переменных, даже в том случае, когда не все из них влияют на положение экстремума целевой функции и часть из них можно не варьировать в процессе оптимизации.

3.Параметры УЦОС (многие из которых нелинейно зависят от других параметров) в

процессе оптимизации можно варьировать лишь в определенных пределах, то есть требуется соблюдать большое число ограничений. Эти ограничения существенно затрудняют выбор и работу методов оптимизации, и, главное, осложняют процесс формализации и сведения каждой конкретной задачи к общей задаче, описываемой в терминах математического программирования.

4.Однократное вычисление целевых функций в задачах оптимизации УЦОС связано с достаточно сложным и трудоемким решением соответствующей задачи расчета их характеристик. Наиболее эффективными являются алгоритмы, которые в процессе оптимизации наименьшее число раз обращаются к вычислению значений целевых функций,

ограничений и производных для получения решений с требуемой точностью.

91

5.В задачах оптимального проектирования УЦОС большинство реальных целевых функций имеют сложную невыпуклую и не дифференцируемую поверхности, что существенно понижает эффективность стандартных методов нелинейной оптимизации.

6.При проектировании УЦОС целевые функции имеют характерную овражную структуру, что существенно осложняет процесс поиска экстремума, требует применения более сложных и надежных методов оптимизации, которые, в свою очередь, требуют больших вычислительных затрат.

Являясь достаточно универсальными, стандартные методы оптимизации не учитывают указанные выше характерные черты задач проектирования УЦОС, что во многих проектных ситуациях заметно снижает их эффективность. Следовательно, проблемы построения эффективных алгоритмов оптимизации обобщенных критериев и разработки подсистемы оптимизации УЦОС на их основе являются чрезвычайно актуальными.

2. ФОРМИРОВАНИЕ ОБОБЩЕННЫХ КРИТЕРИЕВ ОПТИМАЛЬНОСТИ УЦОС И РАСЧЕТ ИХ ПРОИЗВОДНЫХ

2.1 Формирование обобщенных критериев оптимальности УЦОС

УЦОС характеризуется множеством внутренних варьируемых параметров

предельные значения требований к i - ой выходной характеристике в заданном диапазоне частот. Аналогичные ограничения во временной области могут быть пересчитаны в частотную область на основе известной связи между временной и частотной областями [47,48]. При этом в случае, если требования ЧТЗ задаются в виде «эталонных» характеристик, в (2.1) H нi ( ) = H вi ( ) , для i 1,2, , P .

Представим неравенство (2.1) в векторной форме

e(X , ) 0,

где

e(X , ) {e1 (X , ),e2 ( X , ), , eP ( X , )} .

92

Совокупность отклонений ei (X , ) от заданных границ можно представить разными

работоспособности для i -ой ЧХ УЦОС при произвольных значениях компонент вектора

X D , где D - область допустимых значений. Наилучшим (оптимальным) УЦОС будет

Выражение Ошибка! Источник ссылки не найден. фактически представляет собой

задачу векторной оптимизации, решение которой во многих случаях удается свести к решению ряда задач скалярной оптимизации, где в качестве целевой функции используется тот или иной обобщенный критерий оптимальности [1, 7 – 11, 13 - 14, 17, 19 - 20].

Правильный выбор обобщенного критерия оптимальности в каждом конкретном случае весьма важен, поскольку он определяет адекватность математической постановки задачи и реальной проектной задачи. Рассмотрим алгоритмы формирования базового набора обобщенных критериев оптимальности УЦОС.

Очевидно, что скаляризация задачи векторной оптимизации сводится в рассматриваемом случае к формированию обобщенного критерия Q(X ) ). Связь Q(X ) с

функцией e(X , ) определяется выбранной нормой. Если эту связь представить как

Q( X ) e( X , ) L ,

то формулировка задачи скалярной оптимизации имеет вид

93