Методы оптимального проектирования устройств цифровой обработки и защиты информации. Борисов В.И., Гармонов А.В

Оформление. Воронежский государственный технический университет, 2002

ВВЕДЕНИЕ

Для построения устройств обработки и защиты информации широко используются устройства цифровой обработки сигналов (УЦОС). Обычно оптимальное проектирование УЦОС осуществляется по одному наиболее важному показателю качества. Такой подход не гарантирует обеспечение других требуемых характеристик и часто приводит к нереализуемым с точки зрения заданных параметров устройствам обработки. Это вызвано специфическими особенностями проектируемых устройств, связанными с множественностью, а зачастую и противоречивостью предъявляемых к ним требований,

неопределенностью условий их функционирования, высокой чувствительностью получаемых решений и рядом других факторов. Эта ситуация наиболее характерна при оптимальном проектировании УЦОС с одновременно заданными несколькими характеристиками.

Совокупность вышеуказанных факторов обуславливает необходимость решения на этапе проектирования УЦОС задач векторной (многокритериальной) оптимизации (ЗВО).

При этом на варьируемые параметры могут быть наложены дополнительные условия,

описываемые соответствующими функциями – ограничениями, отражающими возможность физической реализуемости объекта проектирования, технические условия на проект и т.п.

Таким образом, можно сказать, что обсуждаемые проблемы в действительности формулируются как многокритериальные задачи принятия решения.

Под принятием решения понимается выбор наиболее предпочтительного из множества допустимых альтернативных решений. Этим занимается теория принятия решений при наличии многих критериев.

С многокритериальными задачами радиоинженер встречается повсеместно, если учесть, что при разработке устройств обработки и защиты информации необходимо добиться выполнения множества часто противоречивых требований, к числу которых относятся:

высокие технические характеристики, низкая стоимость, малая энергоѐмкость и т.д. При этом чем больше показателей качества рассматривается, тем более полная характеристика достоинств и недостатков проектируемого устройства достигается. Отсюда видно, что формулировка корректной математической задачи в реальных условиях весьма трудна, а еѐ решение может представлять ещѐ большие трудности, поскольку нужно найти такой компромисс между критериями, который был бы удовлетворительным с точек зрения

66

проектировщика и заказчика. Здесь следует иметь в виду два обстоятельства: задача должна быть всегда чѐтко очерчена; в рамках этой задачи необходимо ставить некоторую глобальную цель. Это означает принятие не просто какого-то, пусть и конкретного,

компромиссного решения, но решения оптимального.

Предлагаемое пособие преследует цель ознакомить студентов с математическими проблемами векторной оптимизации. Под векторной оптимизацией понимается прикладная наука, связанная с моделированием выбора и, в частности, со следующими проблемами:

выяснения и формализации параметров выбора, ограничений (исходного множества вариантов и альтернатив), структуры предпочтений, построения алгоритмов выбора,

оперирующих с этой информацией, оценки точности таких алгоритмов и т.п.

В теории принятия решений вместо целевой функции задается отношение предпочтения на множество возможных результатов, т.е. указывается, какая их совокупность соответствует цели больше, а какая меньше. Само отношение предпочтения должно задаваться явно. Сделать это в большинстве случаев бывает легче, чем задавать целевую функцию, поскольку здесь требуется не численная оценка, во сколько один результат лучше

(хуже) другого, а лишь показания того какие результаты лучше, а какие хуже.

Центральным в теории принятия решений при неантагонистических ситуациях является принцип компромисса Парето, который исключает из неформального анализа заведомо плохие варианты решений.

Первая глава содержит постановку задачи оптимального проектирования УЦОС с векторной целевой функцией, методику проектирования этих устройств, обзор и анализ методов решения задач векторной оптимизации (ЗВО) и обоснование требований к обобщенным критериям.

Во второй главе рассмотрена процедура построения и исследованы основные структуры обобщенных критериев, используемые при решении ЗВО УЦОС, приведены экономичные алгоритмы расчета передаточных функций фильтров нерекурсивной и рекурсивной структур и их производных, и (на их основе) экономичный алгоритм расчета обобщенных критериев.

Втретьей главе проведены методы решения задачи оптимального проектирования со скалярной целевой функцией, построен комбинированный проблемно-адаптивный алгоритм оптимизации и предложена стратегия его работы.

Вчетвертой главе рассмотрено применение методов оптимизации для решения задач оптимального проектирования УЦОС и устройств защиты информации на их основе.

67

Учебное пособие предназначено для студентов старших курсов, изучающих

дисциплину "Проектирование устройств цифровой обработки сигналов".

ОБЗОР МЕТОДОВ И ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО

ПРОЕКТИРОВАНИЯ УЦОС

1.1Векторная постановка задачи оптимального проектирования УЦОС

Внаиболее общем случае задача проектирования УЦОС сводится к синтезу устройства, отвечающего заданному комплексу требований. Поэтому постановка задачи проектирования заключается в формировании комплекса требований, которые представляют собой частное техническое задание (ЧТЗ) на проектирование. Составление ЧТЗ входит в процесс проектирования, и от правильности решения этой задачи во многом зависят результирующие свойства проектируемого объекта [55].

Рыночные отношения обуславливают необходимость разработки конкурентоспособных УЦОС, спрос на которые будет устойчивым в течении ряда лет.

Поэтому роль процедуры составления ЧТЗ в настоящее время весьма велика. При разработке и согласовании разделов ЧТЗ выявляются проектные, конструктивные и технологические противоречия, успешное разрешение которых является предметом исследования. С одной стороны, ЧТЗ должно соответствовать современным требованиям, с учетом последних достижений в областях теории, технологии и производства, а с другой - ориентация только на перспективные достижения (технологии и технические решения) в условиях недостаточной изученности их особенностей и технологической освоенности может привести к срыву разработки и выпуска этих устройств. Поэтому на этапе формирования ЧТЗ важно не только правильно определить основные цели проектирования, но и указать основные условия и конструктивно-технологические ограничения, которым должны удовлетворять структура и параметры проектируемого устройства. Обычно ЧТЗ на

68

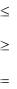
проектирование УЦОС включает несколько разделов, основными из которых являются назначение устройства, совокупность критериев качества, ограничений и т. п.

Конкретные числовые требования целесообразно включать во все разделы ЧТЗ, кроме критериев качества (оптимальности). Это обеспечивает достаточно полную реализацию возможностей проектировщика (интеллектуальных, технологических, информационных и др.). Наличие ряда характеристик устройства в составе ненормированных критериев качества обуславливает многовариантность проектирования и обеспечивает обоснованность выбора одного или нескольких перспективных технических решений. Кроме того, ненормированные критерии качества и их оптимизация позволяют выявить противоречия при проектировании

и привести к необходимости проектирования УЦОС на уровне изобретения.

ЧТЗ должно включать в себя группы технических требований, предъявляемые к основным характеристикам устройства; конкретные числовые данные, характеризующие условия сопряжения УЦОС с соседними каскадами; требования к экономическим и

эксплутационным характеристикам объекта проектирования; конструктивно-

технологические ограничения на внутренние варьируемые параметры; качественное описание требований, ограничений и условий, непосредственно не поддающихся количественной оценке [54, 55].

Первые три группы требований могут быть представлены количественно. Последняя группа требований представляет собой качественную сторону объекта проектирования.

Таким образом, все требования ЧТЗ делятся соответственно на количественные и

качественные.

Требования количественного характера поддаются формализации и в окончательном виде представляют собой совокупность (вектор) TT=( T1 ,T2 , ,Tm ) технико-экономических требований T1 ,T2 , ,Tm , где число m может быть достаточно большим (например, больше

десяти). Технико-экономические требования могут иметь один из следующих видов [55]

где Yj - j -ый выходной параметр (показатель качества) УЦОС; Tj - техническое требование или норма j -го выходного параметра.

Совокупность требований, накладываемых на проектируемое устройство, наряду с другими условиями, обуславливают многокритериальный (векторный) характер задачи

69

проектирования сложного технического устройства [7 - 11], в том числе и УЦОС.

Требования ЧТЗ качественного характера порождают на этапе формирования формализованного ЧТЗ проблему нечеткости исходной проектной информации. Проблема формализации информации качественного (нечеткого) характера решается на основе понятия нечеткости [56,57]. Таким образом, несмотря на наличие определенных трудностей,

проблема формализации требований ЧТЗ количественного и качественного характера в общем случае является разрешимой задачей. Рассмотрим формализованную постановку задачи оптимального проектирования УЦОС.

Пусть проектируемое УЦОС определяют N варьируемых параметров Х1, Х2,…, ХN,

которые будем считать точкой в N - мерном пространстве EN. Обычно в качестве вектора варьируемых параметров принимаются коэффициенты передаточной функции УЦОС.

Для того, чтобы спроектировать оптимальное устройство, необходимо в процессе его проектирования учесть три сорта ограничений - параметрические, функциональные и критериальные [85].

Параметрические ограничения имеют вид

где X нi , X вi - нижние и верхние предельные значения для i -го варьируемого параметра. В

более общем случае границы интервалов могут быть функциями от других варьируемых параметров

Ошибка! Источник ссылки не найден., Ошибка! Источник ссылки не найден. часто бывают вызваны конструктивно-технологическими требованиями ЧТЗ на проектирование.

Функциональные и критериальные ограничения накладываются на выходные параметры устройства. Функциональные ограничения включают в себя условия работоспособности, имеющие принципиальное значение при оценке правильности функционирования устройства исходя из целей проектирования и выполнения устройством своего функционального назначения [7]. Эти ограничения можно записать так:

70

Условие Ошибка! Источник ссылки не найден. представляет собой, по существу,

условие устойчивости фильтра, а условие Ошибка! Источник ссылки не найден. является условием физической реализуемости фильтра.

Следующая группа ограничений накладывается на выходные параметры, имеющие смысл локальных (частных) критериев оптимальности (ЛКО) и характеризующие качество объекта проектирования. ЛКО Qi , i =1,…, M являются такие показатели качества конкретного устройства, которые [7 – 11, 19 - 20, 85]:

-связаны с качеством УЦОС монотонной зависимостью (чем меньше или больше критерий, тем лучше устройство при прочих равных условиях);

-достаточно полно характеризуют исследуемое УЦОС;

-отражают интересы заказчика;

-дают возможность выбора оптимального или приемлемого варианта построения устройства;

-являются обозримыми и удобными для вычисления;

-характеризуют ценность решений таким образом, чтобы у проектировщика имелось стремление получить по ним наиболее предпочтительные оценки.

ЛКО зависят от структуры УЦОС и от совокупности (множества) N параметров,

(максимальное) значение данного критерия. Трудность заключается в том, что для некоторых локальных критериев может существовать свой оптимальный вектор параметров

X. Вектор ЛКО бывает либо задан, либо формируется в процессе исследования. Для каждого ЛКО Qi указывается шкала (подмножество) Gшi, из которого он принимает свои значения.

В практических задачах проектирования УЦОС формирование набора ЛКО является достаточно трудной проблемой и поэтому требует специального рассмотрения. Один из подходов образования векторного критерия заключается в том, чтобы прежде всего составить по возможности наиболее полный перечень локальных критериев и только затем (в

процессе постановки, решения и анализа конкретной задачи проектирования) исключить из рассмотрения несущественные критерии.

Рассмотрим способы формирования наиболее важных ЛКО УЦОС на примере проектирования цифровых фильтров (ЦФ). Основой для формирования ЛКО рассматриваемых устройств является ЧТЗ. Оно содержит требования к амплитудно –

71

частотной характеристике (АЧХ), фазочастотной характеристике (ФЧХ), характеристике группового времени задерживания (ГВЗ), переходной и импульсной характеристикам (ПХ,

ИХ), стабильности частотных характеристик (ЧХ), объему алгебраических операций сложения и умножения при аппаратной реализации ЦФ, стоимости, конструктивно-

технологические требования и ряд других.

В общем случае, в зависимости от конкретных требований ЧТЗ, оптимальность АЧХ проектируемого ЦФ можно оценивать следующими локальными критериями [7, 15, 33, 36, 38 - 40, 47 – 48, 58, 61, 72, 86] : неравномерностью АЧХ в полосе пропускания; подавлением боковых лепестков АЧХ в полосе задерживания; шириной переходной полосы АЧХ;

шириной полосы пропускания АЧХ по уровню 3 дБ; шириной полосы пропускания АЧХ,

например, по уровню 40 дБ; коэффициентом прямоугольности по заданным уровням;

нестабильностью АЧХ в заданной частотной точке или заданном частотном диапазоне.

Неравномерность АЧХ в полосе пропускания вычисляется по формуле:

где En - множество частот в полосе пропускания.

Подавление боковых лепестков АЧХ в полосе задерживания вычисляется по формуле:

где Eз – множество частот в полосе задерживания.

Контроль ширины переходной полосы АЧХ удобно осуществлять, используя

где 3 - частота среза; 4 - граничная частота полосы задерживания.

Вид критерия Q3 ( X ) исключает возможность получения функции с минимумом в

отрицательной области частот. При этом считается, что поведение АЧХ в переходной полосе

72

требований ЧТЗ по обеспечению требуемой ширины полосы пропускания по заданному заказчиком уровню. Наиболее часто ширина полосы пропускания АЧХ контролируется по уровню 3 дБ. Аналогичным образом можно ввести локальные критерии для контроля выполнения требований ЧТЗ к ширине полосы пропускания АЧХ по любому другому уровню, например 6 дБ, 40 дБ или 60 дБ. Все эти критерии вычисляются численно после расчета АЧХ. В ряде случаев для оценки оптимальности АЧХ используют коэффициент прямоугольности по заданным уровням, например, 3 дБ и 40 дБ, вычисляемый по формуле:

характеристик при воздействии различных дестабилизирующих факторов (температура,

старение, радиация и т.п.) [90]. Она зависит, в основном, от структуры устройства и значений его внутренних параметров. Меру стабильности АЧХ (ФЧХ, ГВЗ, ПХ, ИХ) ЦФ можно оценивать, например, функционалом вида:

Кроме перечисленных ЛКО большое практическое применение находят также

следующие критерии: - норма отклонения ФЧХ от линейной, Q8 ( X ) -

неравномерность ГВЗ, Q9 ( X ) - норма отклонения характеристики ГВЗ от заданной.

Известные ЛКО жестко связывают относительную форму характеристик и их абсолютные значения. Поэтому в ряде случаев необходима иная, более гибкая структура ЛКО, в которых эти требования можно разделить и задавать их при оптимизации УЦОС с

где 1 и 2 - весовые коэффициенты, а H 0 ( ) - «эталонная» АЧХ.

73