
Решение практических и типовых задач по курсу Линейная алгебра и аналитическая геометрия. Лапшина М.Л
.pdfМ.Л. Лапшина
РЕШЕНИЕ ПРАКТИЧЕСКИХ И ТИПОВЫХ ЗАДАЧ ПО КУРСУ
«ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»
Учебное пособие
Воронеж 2002
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
М.Л. Лапшина
РЕШЕНИЕ ПРАКТИЧЕСКИХ И ТИПОВЫХ ЗАДАЧ ПО КУРСУ
«ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»
Учебное пособие
Воронеж 2002
УДК
Лапшина М.Л. Решение практических и типовых задач по курсу "Линейная алгебра и аналитическая геометрия". Учеб. пособие / Воронеж: Воронеж. гос. техн.
ун-т, 2002, 81с.
В работе изложены основные понятия и теоремы, необходимые для решения практических задач. Пособие содержит большое количество примеров для проведения практических задач и теоретического контроля знаний студентов. Практические задания снабжены необходимыми комментариями и решениями.
Решены наиболее сложные задачи из типовых расчетов.
Учебное пособие предназначено для студентов, обучающихся по специальности 071900 "Информационные системы" при изучении курса "Линейная алгебра и аналитическая геометрия"
Учебное пособие подготовлено на магнитном носителе в текстовом редакторе MS Word 2000 и содержится в файле "Лекция.doc".
Библиогр.: 2 назв.
Научный редактор: п-р. ф-м. Наук И.А.Батаронов. Рецензенты:
1.кафедра теоретической и прикладной механики ВГУ (зав. Кафедрой д-р физ.-мат. наук проф. Спорыхин А.Н. ),
2.к. физ.-мат. наук, доцент Е.Н. Коржов.
Издается по решению редакционно-издательского совета Воронежского государственного технического университета.
©Лапшина М.Л., 2002 г.
©Оформление Воронежский государственный технический университет, 2002.
Введение.
Учитывая недостаточное ограниченное количество аудиторного времени и большое количество теоретического материала, предлагаемого студентам при изучении курса "Линейная алгебра и аналитическая геометрия", автором были подробно рассмотрены задания, предлагаемые студентам для самостоятельной работы.
Для удобства использования пособия каждый раздел содержит необходимый теоретический материал. В конце пособия предложено достаточное количество заданий для проведения контрольных работ, индивидуальных работ студентов и заданий для проведения типовых расчетов
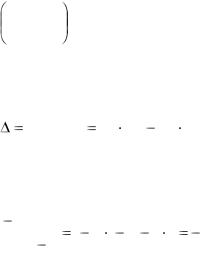
Определители и их свойства.
Определение. Определителем второго порядка соответствующего таблице
|
a11 |
a12 |
|
|
|
|
|
|
(1) |
|
|
a21 |
a22 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
называется число, записываемое в виде |
|
|||||||||
|
|
a11 |
a12 |
|
a11 |
a22 |
a21 |
a12 |
(2). |
|
|
|
|
||||||||
|
|
a21 |
a22 |
|
||||||
Пример. |
|
|
|
|
|
|
|
|||
|
8 |
|
( 3) ( |
6) |
4 8 |
14 |
|
|||
|
3 |
|
|
|||||||
|
4 |
6 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||
Числа aij называются элементами определителя, где первый индекс i указывает номер строки, а j – номер столбца, на пересечении которых находится элемент.
Диагональ, на которой находятся элементы с одинаковыми индексами, называется главной диагональю определителя, а элементы a21 и a12 находятся на побочной диагонали. Порядок определителя определяется числом строк (столбцов). Определителем третьего порядка называется число, обозначаемое символом

|
а11 |
а12 |
а13 |
|
|
|
|
|
|
а21 |
а22 |
а23 |
а11 а22 а33 |
а12 |
а23 |
а31 |
а13 а32 а21 |
|
а31 |
а31 |
а33 |
|
|
|
|
|
а13 а22 а31 |
а12 а21 а33 |
а32 |
а23 |
а11 |
(3). |
|||
Свойства определителей.
1. Величина определителя не изменится, если все его строки заменить его столбцами с теми же номерами, то
|
а11 |
а12 |
а13 |
|
а11 |
а21 |
а31 |
есть |
а21 |
а22 |
а23 |
|
а12 |
а22 |
а32 |
|
а31 |
а31 |
а33 |
|
а13 |
а23 |
а33 |
2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на (-1), то есть
а11 |
а12 |
а13 |
|
а31 |
а32 |
а33 |
а21 |
а22 |
а23 |
|
а21 |
а22 |
а23 |
а31 |
а31 |
а33 |
|
а11 |
а12 |
а13 |
3.Если определитель имеет 2 одинаковых столбца (две строки), то он равен нулю.
4.Умножение всех элементов одного столбца определителя или одной строки на любое число к равносильно умножению всего определителя на это число. Итак, общий множитель всех элементов одного столбца (строки) можно выносить за знак определителя.
5.Если все элементы некоторого столбца (строки) равны нулю, то сам определитель равен нулю.
6.Если два каких либо столбца (строки) пропорциональны, то определитель равен нулю
7.Если все элементы какого-либо столбца (строки) можно представить в виде двух слагаемых, то этот определитель можно представить в виде суммы двух

определителей, из которых один в этом столбце (строке) имеет первые слагаемые, а в другой второе, а элементы, стоящие на остальных местах у всех трех определителей одинаковые, то есть
а / |
а // |
а |
|
а |
|
|
а / |
а |
|
а |
|
|
а // |
а |
|
а |
|
11 |
11 |
12 |
13 |
|
11 |
12 |
13 |
|
11 |
12 |
13 |
||||||
а / |
а // |
а |
22 |
а |
23 |
|
а / |
а |
22 |
а |
23 |
|
а // |
а |
22 |
а |
23 |
21 |
21 |
|
|
|
21 |
|
|
|
21 |
|
|
||||||
а / |
а // |
а |
31 |
а |
33 |
|
а / |
а |
31 |
а |
33 |
|
а // |
а |
31 |
а |
33 |
31 |
31 |
|
|
|
31 |
|
|
|
31 |
|
|
||||||
8. Если к элементам некоторого столбца (строки) прибавить соответствующие элементы другого столбца (строки) умноженные на любой общий множитель, то величина определителя при этом не изменится.
Определение. Минором (Mij) элемента aij называется определитель, полученный из данного путем вычеркивания i-ой строки и j-ого столбца, на пересечении которых находится элемент.
Определение. Алгебраическое дополнение Aij для элемента aij равняется минору этого элемента Mij, взятому со своим знаком, если сумма индексов i+j - четное число и с противоположным знаком, если i+j – нечетное число.
9.Определитель равен сумме произведений
элементов, |
какого-либо |
столбца (строки) |
на их |
алгебраические дополнения. |
|
||
a11 A11 |
a12 A12 a13 |
A13 |
|
Существует несколько методов для вычисления определителей порядка к – рассмотрим один из них: метод понижения порядка определителей, который основан на следующем соотношении
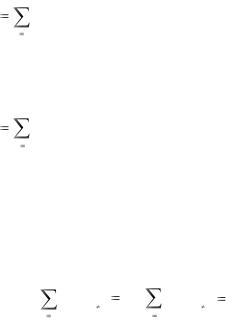
а11 |
а12 |
а13 |
n |
|
|
|
|
а21 |
а22 |
а23 |
аij Aij при фиксированном j разложение |
а31 |
а31 |
а33 |
i 1 |
|
ведется по столбцу с номером j.
а11 |
а12 |
а13 |
n |
|
|
|
|
|
|
а21 |
а22 |
а23 |
|
аij Aij при фиксированном i разложение |
а31 |
а31 |
а33 |
j |
1 |
|
|
ведется по столбцу с номером i.
То есть вычисление определителя порядка n сводится к вычислению n определителей порядка n- 1.
10. Сумма произведений элементов какого-либо столбца (строки) на алгебраические дополнения соответствующих элементов другого столбца (строки)
n |
|
n |
|
|
|
|
равна нулю, то есть aik |
Aij |
0 , |
aij |
Akj |
k |
0 . |
|
k j |
|
|
|
j |
|
i 1 |
|
j |
1 |
|
|
|
Решение систем линейных алгебраических уравнений.
В качестве приложения теории определителей рассматривают решение систем линейных алгебраических уравнений. Пусть дана система из трех уравнений с тремя неизвестными

а11 х1 |
а12 х2 |
а13 х3 |
b1 |
|
|
а21 |
х1 |
а22 х2 |
а23 х3 |
b2 |
(1) |
а31 |
х1 |
а32 х2 |
а33 х3 |
b3 |
|
Определитель, составленный из коэффициентов при неизвестных называется определителем данной системы и выражается
а11 |
а12 |
а13 |
|
а21 |
а22 |
а23 |
(2) |
а31 |
а31 |
а33 |
|
Умножим обе части уравнения 1 системы (1) на А11, второго уравнения на А21, для третьего на А31. Сложим
полученные уравнения и, |
группируя результат, получим |
||||||||
х1(a11 |
A21 a12 A22 |
a31 A32 ) |
|||||||
х2 (a12 A21 |
a22 |
A21 |
|
a32 |
A31) |
||||
х3 (a13 A11 |
a23 |
A21 |
|
a33 |
A31) |
||||
b1 А11 |
|
b А21 |
b3 А31 |
|
|
(3). |
|||
х1 |
1 |
|
|
|
|
|
(4) |
||
х1 |
|
1 |
|
|
|
|
|
|
(5) |
|
|
|
в1 |
а12 |
а13 |
|
|||
|
|
|
|
|
|
||||
где 1 |
|
|
в2 |
а22 |
а23 |
|
|
||
|
|
|
|
в3 |
а31 |
а33 |
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
а11 |
в1 |
а13 |
|||
Аналогично для х |
|
|
2 |
, х |
|
3 |
, где |
|
а |
|
в |
|
а |
|
|||
2 |
|
|
3 |
|
2 |
21 |
2 |
23 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
а31 |
в3 |
а33 |
|||
|
а11 |
а12 |
в1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и 3 |
а21 |
а22 |
в2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а31 |
а31 |
в3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формулы |
(5) |
– формулы Крамера, |
при |
0 , |
а |
|
1 , |
2 , 3 |
получаются из определителя |
путем замены 1, |
|||
2, 3 столбцов столбцами свободных членов. |
|
|
||||
1. |
Формулы |
Крамера справедливы |
для |
систем |
n- |
|
линейных уравнений с n неизвестными, в том случае, если
|
0 , где |
- определитель системы. |
|
||||
2. |
|
Если |
= |
0, а хотя |
бы один |
из определителей |
|
i |
0 |
, то система не имеет решений (говорят, что она |
|||||
|
|
|
|
|
|
|
|
несовместна) |
|
|
|
|
|||
3. |
|
Если |
= |
0, и все |
i |
0 , то |
система не имеет |
|
|
|
|
|
|
|
|
решений или имеет бесконечно много решений (система называется неопределенной)
Исследование однородных систем
Рассмотрим однородную систему из 2 уравнений с тремя неизвестными x, y, z.
а11 х |
а12 у |
а13 z |
0, |
(1) |
|
а21 х |
а22 у |
а23 z |
0 |
||
|
Такая система всегда имеет тривиальное решение x=y=z=0.
Рассмотрим вопрос о нахождении ненулевого решения.
