Методическое пособие 457

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

вектора не коллинеарны.

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.58 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 108 9 10 > Следующая >>>

Исследование и привидение к каноническому виду общего уравнения кривой второго порядка.

a x 2							2a					x x				2			a		22		x		2							2a x								2a			2	x	2	a	0	0	(1)
11			1						12				1			2					22			2											1		1						2		2		0

					группа _ старших
					Пусть a12														0
a x 2							a		22	x			2				2a x 2a														2		x		2			a	0			0
11			1						22			2							1			1									2				2				0
Выделим полные квадраты при х:
					2						a									a		2								a				2
a				x					2			1			x						1												1
a				x					2						x
11			1							a11						1				a			2								a11
										a11										a			2								a11
																					11
		a			x	2				2				a2				x					a2			2										a2		2			a				0
		a	22		x	2				2				a22				x	2				a22				2									a22					a	0			0
			22			2													2																							0

													2																						2
								a																					a			2								a	2				a	2
a11				x1					1								a22					x2										2								1						2	a0
a11				x1				a11									a22					x2						a22												a11					a22		a0

					x1 ''																				x2 ''																				k
Получим a													x ''2						a		22		x	2	''2									k
										11			1								22			2
	x ''2					x		2	''2
1								2							1		- канонический вид кривой второго пор-ка.
		k						k							1		- канонический вид кривой второго пор-ка.
		k						k

		a11					a22

Пусть кривая задана общим уравнением (1), поставим в соответствие группе старших членов симметричную матрицу S. Найдем собственные числа и собственные векторы этой матрицы. Получим:

	a11	a12	a1 '	a2 '


S''	a12	a22	, 2 a1 B11 a2 B22	2 a1 B12 a2 B22

1	x '2		2	x	2	'2	2a (B B )x ' 2a				2	(B B )x		2	' a	0	0
		1					1	11	21	1		12	22
1 ,		2 - собственные числа матрицы S.
x1 ', x2 '			- координаты в навой системе, определенной
базисом из собственных векторов матрицы S.

	X					x1 ,								X '		x1 ' ,								X BX '
						x2										x2 '
		x1								B11				B12	x1 '
		x2							B21					B22	x2 '
2a1 x1 ' B11														x2 ' B12			2a2 x1 ' B21 x2 ' B22
1			x '		2					2	x	2	'2 2a ' x ' 2a								2	' x		2	' a		0	0
1				1						2		2		1	1						2			2			0
(4)
												Уравнение (4) приведем к каноническому виду
путем выделения полного квадрата:
													2										2
								a '											a	2		'				a '2			a	2	'2
				x1 '						1					x2					2							1			2		a0
1				x1 '										2	x2																	a0
										1											2						1				2

						x1 ''											x2 ''												k
Получим												1		x ''2	2	x	2	''2					k
												1		1	2		2
	x ''2						x			2	''2
1										2				1
		k								k				1
		k								k

			1								2
(5)
						Матрица В является матрицей поворота на угол
	B				cos									sin
	B				sin									cos
					sin									cos

Для того, чтобы привести общее уравнение кривой второго порядка к каноническому виду, нужно:

1.В соответствие группе старших ставим симметричную матрицу S.

2.Найти собственные числа и собственные векторы матрицы S.

3.Введем новые координаты, взяв в качестве базиса орты собственных векторов матрицы S.

4.После введения нового базиса, при котором исчезнут произведения текущих координат, общее уравнение кривой примет вид:

1	x '2	2	x	2	'2	2(a t	a	t	21	)x ' 2a	2	(a t	a	t	22	)x	2	' a	0	0
1	1	2		2		1 11	2		21	1	2	1 12	2		22		2		0

Введение нового базиса равносильно повороту системы координат на угол .

x1	x1 'cos	x2	'sin	формулы поворота.
x2	x1 'sin	x2 'cos

Исследование общего уравнения кривой по ее коэффициентам.

x ''2		x	2	''2				a '2	a	2	'2
1			2		1	,	k	1		2		a0
	k		k		1	,	k	1			2	a0
	k		k

1 2

1 , 2 - решения характеристического уравнения.

1	,	2	a	a	22	a	2	(по теореме Виета)
1		2	11		22	12
		1.	Пусть			1	2	0
						1	2
			а)		1	2	0 , т.е. знаки совпадают		–	кривая
					1	2
			эллиптического типа.
						если знак k совпадает со знаками			1 ,	2 , то –
						эллипс.

знак k не совпадает – уравнение мнимого эллипса

k=0 – точка

б)	1	2	0 - кривая гиперболического типа

если знак k совпадает со знаками 1 , 2 , то – гипербола.

k=0 – пара пересекающихся прямых. 2. Пусть 1 2 0 уравнение параболического типа

Примеры решения некоторых задач из типовых расчетов по курсу "Линейная алгебра и аналитическая геометрия".

1. Написать разложение вектора c по базису из векторов p, q, r , если

c	11, 6,5 , p			3,	2,1 , q				1,1,		2	,		2,1,	3 .
c	11, 6,5 , p			3,	2,1 , q				1,1,		2	,	r	2,1,	3 .
а) По определению:
						3 1		2	2	3		0
1 p	2 q	3		0		2 1						0 , где			1 ,	2 , 3 -
1 p	2 q	3	r	0		2 1			2		3	0 , где			1 ,	2 , 3 -
						1	2	2	3	3		0
решения однородной системы.
	3	1		2
	2	1		1	8	0
	1	2		3
	0 , то однородная система имеет единственное
решение						0 ,	т.е.		вектора					p, q,		линейно
решение		1		2	3	0 ,	т.е.		вектора					p, q,	r	линейно
		1		2	3

независимы и образуют базис в пространстве. Столбцы определителя – координаты соответствующих векторов.

б) Запишем разложение вектора c по базису из векторов p, q, r :

							3 1		2		2	3	11
c	1 p		2q	3			2 1						6
c	1 p		2q	3		r	2 1			2		3	6
							1	2	2		3 3		5
	1	2 2		3 3			5	1		2 2			3 3	5
	2 1		2	3			6		2		5	3	4
	3 1		2	2 3			11	5 2			11 3		4
	1	2	2	3 3			5	1	2		2	3 3		5
	2		3	4					2		3		4
	2		3						2		3
	3	2	5	3		4		8	3			8
c	2 p	3q
c	2 p	3q			r

2 3 1

2.Коллинеарные ли вектора c1 и c2 , построенные по

векторам a и b ?

1,2, 1 , b

7,1 , c1 6a

2b , c2

b .

а) Найдем координаты векторов c1

и c2 :

6,12,

6 ,

14,2

10,26,

10 , c2

3a b

18,10 .

По определению коллинеарности двух векторов их текущие координаты должны быть пропорциональными.

3.Найти косинус угла между векторами AB и AC ,

если A		2,4, 6	, B 0,2,	4 ,	C 6,8,	10 .
а)		Найдем			координаты		вектора

	AB 0	( 2),2	4, 4	( 6)	2,	2,2 , AC	8,4, 4


						AB AC
По определению cos(AB				AC)		AB AC


					AB			AC
2 8	( 2) 4	2	( 4)
2 8	( 2) 4	2	( 4)				0


22 ( 2)2	22	82	42 ( 4)2
22 ( 2)2	22	82	42 ( 4)2

cos(AB AC) 90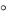

4.Вычислить площадь параллелограмма,

построенного

на

векторах

3b и 3a

b ,

если

1, a ^ b

По

определению

векторного

произведения

a b

(a 3b ) (3a b) 3 * 0 a b 9a b 3 * 0

8a b

4 (кв. ед.)

8 * sin(30 )

Компланарны ли вектора a , b ,

7,4,6 , b

2,1,1 , c

19,11,17 .

По определению вектора компланарны, если определитель, составленный из координат перемножаемых векторов равен 0.

	7	4	6
	2	1	1	(1 7 17)		(4 1 19)		(2 11 6)
	19	11	17
(19 1 6)			(11 1 7)		(2 8 17)		288

Векторы не компланарны.

6. Вычислить объем тетраэдра с вершинами в точках A1 , A2 , A3 , A4 и его высоту, опущенную из вершины A4 на

грань A1 A2 A3 .


A1 (1, 1,2) , A2 (2,1,2) ,	A3 (1,1,4) , A4 (6,	3,8) .
а) Объем тетраэдра	равен 1/6 объема параллелепипеда,

построенного на векторах A1 A2 ,			A1 A3 , A1 A4 . Объем

соответствующего параллелепипеда вычисляется через смешанное произведение соответствующих векторов. Найдем их координаты.

A1 A2 1,2,0 , A1 A3 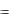0,2,2 , A1 A4 5, 2,6 .

	1	2	0

A1 A2 A1 A3 A1 A4	0	2	2	12 .
	5	2	6

V					1			12				2(куб.ед)
V								12				2(куб.ед)
	тетр				6
					6
б) Искомую высоту найдем по формуле Vтетр																						1	Sосн	h
б) Искомую высоту найдем по формуле Vтетр																						3	Sосн	h
																						3
Sосн					S A A A								1		Sпараллелограмма
Sосн					S A A A						2				Sпараллелограмма
					1			2	3		2
					1			2	3
												i			j		k
												i			j		k

	A1 A2					A1 A3						1 2 0						4i 2 j 2k
												0			2		2
							1
	S	A A A					1			A A A A								1/ 2 16 4 4			6 (кв.ед.)
	S									A A A A								1/ 2 16 4 4			6 (кв.ед.)
					2				1		2				1		3
		1	2	3	2
			3Vтетр								6
h			3Vтетр								6					6 (см)
					S
											6
											6
7.					Найти									расстояние от					точки		M 0 (1,	1,2)		до
плоскости,										проходящей через									M1 (1,5,	7) , M 2 (			3,6,3) ,

M 3 ( 2,7,3) .

а) Составим уравнение плоскости, проходящей через три заданные точки

	x 1 y 5 z ( 7)											x 1 y 5 z 7
	3 1 6 5 3 ( 7)								0 ,				4	1		10	0
	2 1 7 5 3 ( 7)												3	2		10
Уравнение плоскости имеет вид 2x														2y z 15 0
б) Расстояние от точки M 0 (1,											1,2) до плоскости M 1 M 2 M 3
находим										по							формуле
		Ax0 By					Cz0 D			2 1 ( 2) 1 1* 2 15
d		Ax0 By			0		Cz0 D			2 1 ( 2) 1 1* 2 15							21

																	5
			A	2	B	2	C	2			2		2	( 2)	2	2
				2		2		2					2		2	2
																1

8. Написать уравнение плоскости, проходящей через A( 1,2, 2) , перпендикулярно вектору BC . B(13,14,1) ,

C(14,15,2) .

а) Найдем координаты вектора BC .

1,1,1 .

13,15

14,2

б)

Искомое

уравнение

плоскости

имеет

вид

A(x x0 ) B( y y0 ) C(z z0 ) 0

1(x

(

1))

1(y

1(z

(

2)) 0

y z 1 0 .

Найти

угол

между

плоскостями

3x y 5

0 и

cos

A1 A2

B1 B2

C1C2

A12

B12

C12

A2 2

B2 2

C2 2

11 5

arccos

10.

Найти координаты точки A ,

равноудаленной от В и

С.

A(x,0,0) , B( 2, 4, 6) , C( 1, 2, 3) .

По условию задачи

. Найдем BA

( 2 x)2

( 4 0)2

( 6 0)2

( 2 x)2

1)2

2)2

3)2

(x 1)2 13

( 2 x)2

50 ( x 1)2

A( 20,0,0) .

11.

Написать

каноническое

уравнение

прямой

2x 3y 2z 6 0 , x 3y z 3 0

Найдем вектор

nk , параллельный

искомой

прямой. Так как он должен быть перпендикулярен к

нормальным векторам

N1 2i 3 j 2k и N 2 i 3 j k ,

заданных плоскостей, то за S можно принять векторное

произведение N1

и N 2 .

S N1 N 2

13i 8 j 3k

Таким образом l = 13, m = -8, n = -3.

12.В качестве точки M1 (x1 , y1 , z1 ) , через которую

проходит искомая прямая, можно взять точку пересечения ее с любой из координатных плоскостей, например с yOz. Так как x1 0 , то y1 и z1 определим из системы

уравнений, заданных плоскостей, если в них положить x=0:

3y 2z 6 0

3y z 3 0

Решая эту систему, находим y1 4 3 , z1 2

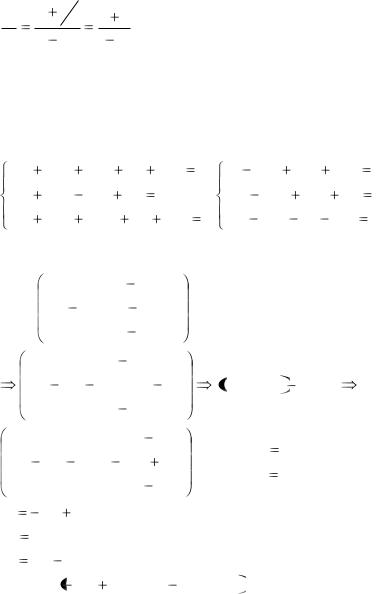
x y 43 z 2

13. Найти общее решение для каждой из данных систем и проанализировать ее структуру (указать базис пространства решений однородной системы, установить размерность пространства, выделить частное решение неоднородной системы).

3x1		2x2		4x3		x4	2x5			0 x1	2x2			3x3	4x4	1
3x1		2x2	2x3			x4	0			4x1	7x2			2x3	x4	3
3x1		2x2	16x3			x4	6x5			0 3x1	5x2			x3	3x4	2
		Составим определитель из координат векторов и
проверим образуют ли они

		1	1		2	2	3	0
базис		2	2		5	1	3	0
		1	1		4	5	6	0
	1	1	2			2	3		0
	1	1	2			2	3		0
	0	4	1			3	3		0	x1 , x2 , x3				базис
	0	0	1			3	3		0
1		1	3			2x4	3x5				x4	t1
1		1	3			2x4	3x5
0		4	1			3x4	3x5			. Пусть				, тогда
0		4	1			3x4	3x5			. Пусть	x5	t		, тогда
0		0	1			3x4	3x5				x5	t	2
x1		7t1	6t2
x2	0
x3	3t1 3t2
Ответ :			7t1		6t2 ;0;3t1				3t2 ; t1 ; t2

<<< < Предыдущая 1 2 3 4 5 6 78 / 108 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.54 Mб2Методическое пособие 452.pdf
#
30.04.20221.56 Mб2Методическое пособие 453.pdf
#
30.04.20221.56 Mб3Методическое пособие 454.pdf
#
30.04.20221.57 Mб24Методическое пособие 455.pdf
#
30.04.20221.57 Mб21Методическое пособие 456.pdf
#
30.04.20221.58 Mб15Методическое пособие 457.pdf
#
30.04.20221.6 Mб14Методическое пособие 458.pdf
#
30.04.20221.6 Mб14Методическое пособие 459.pdf
#
30.04.2022445.95 Кб79Методическое пособие 46.doc
#
30.04.2022307.15 Кб16Методическое пособие 46.pdf
#
30.04.20221.6 Mб15Методическое пособие 460.pdf