
Методическое пособие 457
.pdf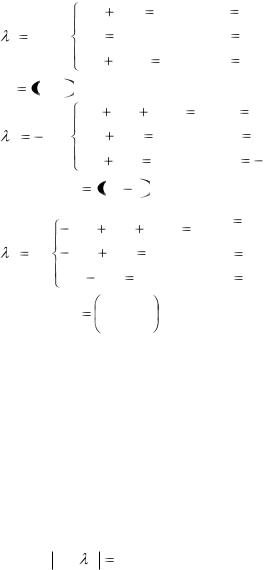
|
|
|
|
|
|
|
4x2 |
7x3 |
0 |
|||
1. |
1 |
1. |
|
|
3x2 |
0 |
|
|
|
|||
|
|
|
|
|
|
|
8x2 |
23x3 |
0 |
|||
|
|
|
|
1,0,0 . |
|
|
|
|
|
|
|
|
|
b1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
3x1 |
|
8x2 |
23x3 |
||
2. |
2 |
2 . |
|
|
7x2 |
7x3 |
0 |
|||||
|
|
|
|
|
|
|
3x2 |
3x3 |
0 |
|||
|
образом, |
|
|
|
|
|
|
|
|
|||
|
b2 |
5,2, |
|
1 |
|
|||||||
|
|
|
|
|
7x1 |
|
8x2 |
|
23x3 |
|||
3. |
3 |
8 . |
3x2 |
|
7x3 |
|
0 |
|||||
|
|
|
|
3x2 |
7x3 |
0 |
|
|||||
|
образом, |
|
|
|
125 |
,7,3 |
||||||
|
b |
|
||||||||||
|
|
|
||||||||||
|
|
|
|
|
3 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
1 |
|
|
|
|
x2 |
0 . Таким образом, |
|||
|
x3 |
0 |
|
|
|
0 x1 |
5 |
|
|
||
|
x2 |
2 |
|
. Таким |
|
|
x3 |
1 |
|
||
|
x1 |
125 |
|
||
0 |
|
|
|
|
|
7 |
|
|
|||
|
|
|
|||
|
|
|
|
||
|
x2 |
7 |
|
. Таким |
|
|
x3 |
3 |
|
|
|
Вывод. Собственные значения линейного оператора совпадают с корнями характеристического уравнения матрицы этого оператора. Каждый линейный оператор имеет собственное значение, так как в силу основной теоремы алгебры характеристическое уравнение всегда имеет корень.
Отметим следующие важные теоремы. Характеристический многочлен линейного преобразования не зависит от выбора базиса.
Если матрица А линейного преобразования А является симметрической, то все корни характеристического
уравнения A 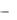 E 0 действительные числа.
E 0 действительные числа.
Лемма. Собственные векторы симметрической матрицы, соответствующие различным собственным числам ортогональны.
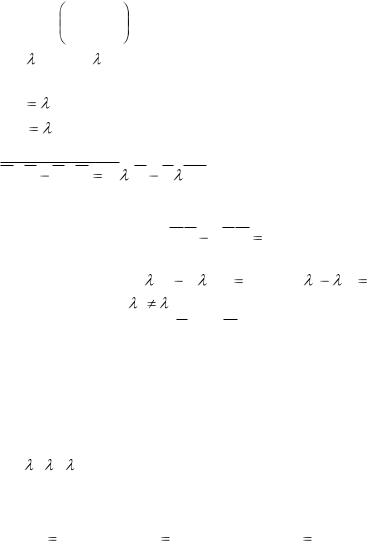
Доказательство приведем для матрицы второго
|
a11 |
a12 . Пусть |
|
|
|
|
|
порядка |
b |
и b |
2 |
- собственные векторы, |
|||
|
a21 |
1 |
|
|
|
||
|
a22 |
|
|
|
|
||
а1 и 2 - соответствующие им различные
действительные числа.
|
|
|
|
|
|
|
|
|
|
|
Ab1 |
b1 |
умножим слева на b2 , |
||||||||
|
|
|
|
|
|
|||||
Ab2 |
|
b2 |
умножим справа на b1 . |
|||||||
Вычтем из верхнего выражения нижнее и получим:
b2 Аb1 b1 Аb2 b2 1 b1 b1 2 b2 . Левая часть равна нулю, так как А – симметрическая матрица, а оператор А
самосопряжен, поэтому скалярное произведение можно
переписать в виде Ab2 b1 Ab1 b2 0 . Таким образом, левая часть равна нулю, следовательно и правая часть
|
|
|
|
|
|
|
|
|
|
|
|
|
равна нулю, тогда b2 |
1 b1 |
b1 2 b2 0 b1 b2 ( 1 |
2 ) 0 , но |
|||||||||
по |
условию |
1 |
2 , |
|
следовательно, |
скалярное |
||||||
произведение векторов b1 и b2 равно нулю, то есть
векторы перпендикулярны.
Вывод: Если матрица симметрическая, то можно говорить об ортогональном базисе, составленном из собственных векторов этой матрицы.
Пусть есть симметрическая матрица третьего порядка.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. 1 , |
2 , 3 |
различны, тогда b1 , b2 , b3 |
будут образовывать |
||||||||||||||||||||
ортогональный базис. Из этого ортогонального можно |
|||||||||||||||||||||||
получить ортонормированный базис. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
b1 |
|
|
|
|
b2 |
|
|
|
|
|
|
b3 |
|
|
|||||
|
b0 |
|
|
b0 |
b0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
b1 |
2 |
|
|
b2 |
|
|
|
|
|
|
|
3 |
|
|
b3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
||||||||
2. |
b3 |
b2 |
b3 b1 , следовательно, |
|||||||||||||||||
|
|
b1 |
|
b2 |
|
b3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
b3 |
плb2 b1 |
|
|
|
|
|
|
|
|
|
|||||||||
Если не все корни характеристического уравнения различны, кратность которых к , то иногда можно указать к линейно-независимых векторов, отвечающих этому собственному значению.
Теорема. Для того чтобы существовал базис из собственных векторов, оператора А необходимо и достаточно, чтобы каждому собственному значению соответствовало столько линейно независимых собственных векторов, какова его кратность. Число линейно-независимых векторов определяется как n – r , где n – размерность матрицы, а r – ее ранг.
Итак, каждому оператору в различном базисе соответствует различная матрица Мы хотим найти такой базис, в котором матрица оператора имела бы простейший вид, а именно диагональный.
В базисе из собственных векторов матрица оператора имеет диагональный вид , где на главной диагонали стоят собственные значения оператора.
|
1 |
0 |
... |
0 |
|
|
|
|
|
||
A |
0 |
2 |
... |
0 |
|
|
|
|
|||
... ... ... ... |
|||||
|
|||||
0 0 ... n
Пример. Найти ортонормированный базис и привести к диагональному виду матрицу.
5 2 2
A 2 2 |
4 . |
2 4 2

1.Составим характеристическое уравнение матрицы
|
5 |
2 |
|
2 |
|
|
|
|
|
|
|
2 |
2 |
|
4 |
0 |
|
|
|
|
(*) |
|
2 |
4 |
|
2 |
|
|
|
|
|
|
|
|
или |
3 |
9 2 |
108 |
0 . |
|
|
|
|
2. |
Корни уравнения |
1 3 , |
2 = |
3 =6. Подставим |
||||||
|
|
|
|
|
|
|
8x1 |
2x2 |
2x3 |
0 |
1 |
3 в (*) и перейдем к системе |
2x1 |
5x2 |
4x3 |
0 . В |
|||||
|
|
|
|
|
|
|
2x1 |
4x2 |
5x3 |
0 |
этой системе первые два уравнения не пропорциональны,
выведем из них x2, x3 |
через x1: |
|||||||||||||
2x2 |
2x3 |
8x1 |
|
|
|
|
|
x2 |
2x1 . Возьмем x1=-1. имеем |
|||||
5x |
2 |
4x |
3 |
2x |
|
|
|
|
|
x |
3 |
2x |
||
|
|
1 |
|
|
|
|
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
||||
собственный вектор a1 |
|
1;2;2 , после нормирования |
||||||||||||
|
|
|
1 |
; |
2 |
; |
2 |
|
|
|||||
получим e |
|
|||||||||||||
|
|
|
|
|||||||||||
|
|
|
1 |
3 |
3 |
|
|
3 |
|
|
||||
|
|
|
|
|
|
|
|
|||||||
Подставим |
3 = 6 в (*) и перейдем к системе |
|||||||||||||
x1 |
2x2 |
2x3 |
0 |
|
|
|
|
|
|
|
||||
2x1 |
4x2 |
4x3 |
0 . Второе и третье уравнения системы |
|||||||||||
2x1 |
4x2 |
4x3 |
0 |
|
|
|
|
|
|
|
||||
пропорциональны первому, следовательно, переходим к
уравнению |
|
x1 2x2 2x3 |
0 . Возьмем любое решение |
||||||
этого уравнения, например |
2; 1;2 .нормируя его, имеем |
||||||||
|
|
|
2 |
; |
1 |
|
2 |
. |
|
|
e2 |
; |
|
||||||
|
3 |
3 |
3 |
|
|||||
|
|
|
|
|
|
||||

e3 находим как смешанное произведение e2 и e1 =
32 ; 32 ; 13 . Таким образом, в базисе из векторов матрица
3 0 0
имеет вид 0 6 0 . 0 0 6
Евклидово Пространство
Линейное пространство R называется евклидовым, если имеется правило, которое позволяет для каждых двух векторов х и у из R построить действительное число, называемое скалярным произведением векторов х и у и обозначаемое (х, у), причем это правило удовлетворяет следующим условиям:
1°. (х, у) = (у, х);
2°. (x, y+z)=(х, у)+(х, z);
3°. |
( x , у)= (х, у) |
для любого Действительного числа , |
4°. |
(х, х) > 0, если х |
0. |
Из условий 1°—4° следует, что:
а) (у+z, х)=(у, х)+(z, х); б) (х, у)= 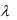 (х, у);
(х, у);
в) (0, х)=0 для любого вектора х.
Скалярное произведение любого вектора x R на себя называется скалярным квадратом вектора х.
Длиной вектора х в евклидовом пространстве называется квадратный корень из скалярного квадрата
этого вектора, |
т. е. |
x |
|
x, x |
|
Если k |
любое действительное число, а х—любой |
||||
вектор евклидова пространства, то |kх| = |k||х |.

Вектор, длина которого равна единице, называется
нормированным. Если |
|
|
x R ненулевой вектор, то |
|||
нетрудно видеть, что |
|
1 |
|
|
x |
|
|
|
x |
|
|
||
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
является нормированным вектором.
Для любых двух векторов х и у в евклидовом пространстве выполняется неравенство x, y 2 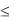 x, x
x, x y, y
y, y
называемое неравенством Коши—Буняковского. Равенство (х, у)2 = (х, х) (у, у) имеет место тогда и
только тогда, когда векторы х и у линейно зависимы.
Из неравенства Коши—Буняковского следует, что
1 |
|
|
x, y |
1. |
Угол |
определяемый |
равенством |
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
y |
|
|
|
|||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
cos |
|
|
(x, y) |
и принадлежащий отрезку [0, 1], называется |
||||||||||
|
|
|
|
x |
|
y |
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
углом между векторами х и у. Если х и у—ненулевые векторы, а 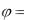 / 2 , то (х, у) = 0. В этом случае говорят,
/ 2 , то (х, у) = 0. В этом случае говорят,
что векторы х и у ортогональны..
Для произвольных векторов х и у евклидова пространства имеют место следующие важные соотношения:
1. |х + у| |х]+|у| (неравенство треугольника). 2. Пусть ф—угол между векторами х и у; тогда
x y |
|
2 |
|
x |
|
2 |
|
y |
|
2 |
2 |
|
x |
|
y |
|
cos |
(теорема косинусов). Если х |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
у, то получается равенство |
|
x y |
|
2 |
|
x |
|
2 |
|
y |
|
2 . Заменяя |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
впоследнем равенстве у на -у, получаем
xy 2 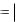 x 2
x 2 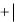 y 2 (теорема Пифагора).
y 2 (теорема Пифагора).

Квадратичные формы
Квадратичной формой действительных переменных
x1 , x2 ,..., xn называется |
многочлен |
второй |
степени |
относительно этих переменных, не содержащий свободного члена и членов первой степени.
|
Если |
|
|
f (x1 , x2 ,..., xn ) |
|
|
квадратичная |
форма |
|||||||||||
переменных |
|
|
x1 , x2 ,..., xn , |
|
|
а |
|
|
|
— |
|
какое-нибудь |
|||||||
действительное |
|
|
|
|
|
|
|
число, |
|
|
то |
||||||||
f ( x , |
x |
2 |
,..., |
x |
n |
) |
|
2 f (x , x |
2 |
,..., x |
n |
) |
|
|
|
|
|
||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
Если n=2, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
f x , x |
2 |
a x 2 |
|
|
2a x x |
2 |
a |
22 |
x 2 |
|
|||||
|
|
|
|
|
|
1 |
11 |
1 |
|
|
12 |
1 |
|
2 |
|
||||
Если n=3, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
f x1 , x2 , x3 |
a11x1 |
a |
22 x2 |
a33 x3 |
2a12 x1x2 2a13 x1x3 |
2a23 x3 x2 |
|||||||||||||
В дальнейшем все необходимые формулировки и определения приведем для квадратичной формы трех переменных.
Матрица
a11 |
a12 |
a13 |
A a21 |
a22 |
a23 |
a31 |
a32 |
a33 |
у которой aik aki называется |
матрицей квадратичной |
|
формы f (x1 , x2 ,..., xn ) , а соответствующий определитель — определителем этой квадратичной формы.

Так как А - симметрическая матрица, то корни 1 , 2 , 3 характеристического уравнения
a11 |
a12 |
a13 |
|
a21 |
a22 |
a23 |
0 |
a31 |
a32 |
a33 |
|
являются действительными числами.
Формулы преобразования координат при переходе к новому ортонормированному базису имеют вид
x1 |
b11 x1 |
b12 x2 |
b13 x3 |
x2 |
b21 x1 |
b22 x2 |
b23 x3 |
x3 |
b31 x1 |
b32 x2 |
b33 x3 |
Преобразовав с помощью этих формул квадратичную форму f (x1 , x2 ,..., xn ) , получаем квадратичную форму
f x1 , x2 , x3 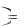 1 x12
1 x12 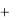 2 x22
2 x22 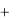 3 x32
3 x32
не содержащую членов с произведениями x1 x3 , x1 x3 , x2 x3 .
Принято говорить, |
что квадратичная |
форма |
f (x1 , x2 ,..., xn ) приведена к |
каноническому |
виду с |
помощью ортогонального преобразования В. Рассуждения проводились в предположении, что характеристические числа 1 , 2 , 3 различны.
При решении задач будет показано, как следует поступать, если среди характеристических чисел имеются одинаковые.
Квадратичные формы 2-х переменных, приведение их к каноническому виду.
Определение: Квадратичной формой двух переменных K (x1 , x2 ) называется однородный многочлен второй степени вида
K (x , x |
2 |
) a x 2 |
2a x x |
2 |
a |
22 |
x |
2 |
||
1 |
11 |
1 |
12 |
1 |
|
|
2 |
|||
(1)
Определение: Однородным многочленом степени k называется многочлен, удовлетворяющий соотношению
P(tx , tx |
2 |
) |
t k p(x , x |
2 |
) |
1 |
|
1 |
|
Представим (1) в виде скалярного произведения. Поставим в соответствие этой квадратичной форме симметричную матрицу S, составленную из координат квадратичной формы.
S |
a11 |
a12 |
|
X |
|
x1 |
|
|
|
|
|
a12 |
a22 |
|
|
x2 |
|
|
|
||||
|
|
|
|
|
|
|
|||||
SX |
a11 |
a12 |
|
x1 |
|
|
|
a11 x1 |
a12 x2 |
|
|
a12 |
a22 |
|
x2 |
|
|
a12 x1 |
a22 x2 |
|
|||
|
|
|
|
|
|||||||
(SX X ) |
(a11 x1 |
a12 x2 )x1 (a12 x1 |
a22 x2 )x2 |
||||||||
a x 2 |
2a x x |
2 |
a |
22 |
x |
2 |
K (x , x |
2 |
) |
||
11 |
1 |
12 |
1 |
|
|
2 |
1 |
|
|||
Т.о. K (x1 , x2 ) (SX , X )
Посмотрим, как изменится координатная форма, а следовательно и матрица S при переходе к новому базису. Для этого воспользуемся следующей леммой.
Лемма: Если оператор А* сопряжен оператору А, то для любых x, y E - эвклидово пространство
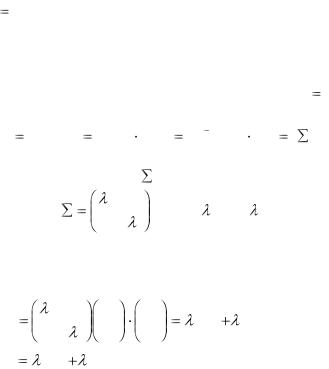
( Ax, y) |
|
(x, AT y) , |
где А – |
матрица оператора |
А, |
АТ |
– |
|
матрица оператора А*. |
|
|
|
|
|
|||
Пусть в базисе e1 , e2 |
k(x1 , x2 ) имеет вид |
(1), |
а |
|||||
соответствующая |
матрица вид |
(2). Перейдем |
к |
базису |
||||
e1 ', e2 ' . Известно, что при переходе |
X |
BX ' , |
||||||
следовательно |
|
|
|
|
|
|
||
K (x , x |
2 |
) (SX , X ) |
(SBX ' BX ') |
(B 1SBX ' X ') |
( |
X ', X ') |
||
1 |
|
|
|
|
|
|
|
|
- квадратичная форма в новом базисе |
|
|
|
|||||
Оказывается, что |
- |
диагональная |
матрица, |
|||||
имеющая вид |
1 |
0 |
, где |
1 и |
2 -собственные |
|
|||||
0 |
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
числа матрицы S.
Найдем вид квадратичной формы в базисе из
собственных векторов( e1 ', e2 ' ): |
|
|
|
|
|
||||||||
k(x ', x |
2 |
') |
|
1 |
0 |
x1 ' |
x1 ' |
1 |
x' 2 |
2 |
x' |
2 |
|
1 |
|
0 |
|
x2 ' |
x2 ' |
1 |
|
2 |
|||||
|
|
|
2 |
|
|
|
|
|
|||||
k(x ', x |
2 |
') |
1 |
x' 2 |
2 |
x' |
2 |
- |
каноническое уравнение |
||||
1 |
|
1 |
|
2 |
|
|
|
|
|
|
|||
квадратичной формы.
Чтобы привести квадратичную форму к каноническому виду (3), нужно:
1.По координатам квадратичной формы составить симметричную матрицу S.
2.Найти собственные числа и собственные векторы матрицы S.
3.Записать квадратичную форму в каноническом виде
(3). Такой вид кв. форма будет иметь в базисе из собственных векторов.
