
Методическое пособие 457
.pdf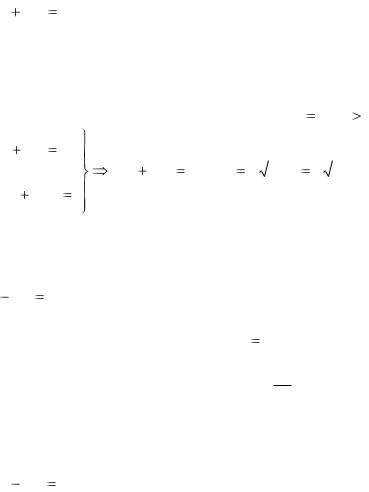
|
|
|
Каноническое |
уравнение |
эллиптического |
|
параболоида имеет вид: |
|
|
||||
|
x2 |
|
y 2 |
z |
|
(5*) |
|
a2 |
|
b2 |
|
||
|
|
|
|
|
||
|
|
|
Плоскости XOZ, |
YOZ являются плоскостями |
||
симметрии. Ось OZ – ось эллиптического параболоида. Из уравнения (5*) следует, что эллиптический параболоид расположен в полуплоскости ZY. Линии пересечения
эллиптического параболоида с плоскостями z |
h , h 0 : |
|||||||||||||||||
|
x 2 |
|
y 2 |
|
h |
|
|
|
|
|
|
|
|
|
|
|
||
|
a 2 |
b2 |
|
x 2 |
|
y 2 |
1, |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
a1 a h,b1 |
b h |
|||||||||||||
|
x 2 |
|
y 2 |
|
|
a 2 |
|
b 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
ha2 |
|
hb2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При увеличении h эллипсы бесконечно увеличиваются. Эллиптический параболоид представляет собой бесконечную чашу. Пусть плоскость x=h
z |
x2 |
|
y 2 |
- уравнение параболы, |
полученной |
||||
a2 |
|
b2 |
|||||||
|
|
|
|
|
|
|
|||
параллельным переносом параболы |
z |
y 2 |
|
при котором ее |
|||||
a2 |
|||||||||
|
|
|
|
|
|
|
|||
вершина (0, 0, 0) переходит в точку (h, 0, h2 ) a2
Каноническое уравнение гиперболического параболоида имеет вид:
x2 |
|
y 2 |
2z |
(6*) |
a2 |
|
b2 |
||
|
|
|
Плоскость XOZ и YOZ являются плоскостями симметрии. Ось OZ – ось гиперболического параболоида.
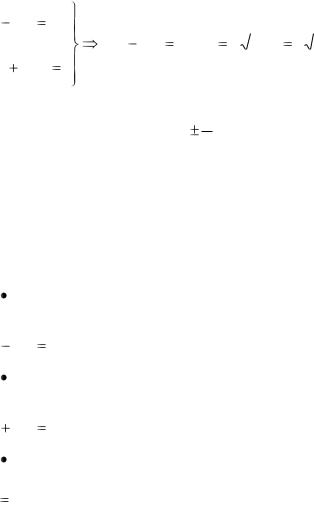
x 2 |
|
y 2 |
|
h |
|
|
|
|
|
|
|
|
|
|
|
||
a 2 |
b2 |
x 2 |
|
y |
2 |
1, |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
a1 a h,b1 |
b h |
|||||||||||||
x 2 |
|
y 2 |
|
a 2 |
|
b 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
ha2 |
|
hb2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Плоскость |
XOY |
|
гиперболический |
параболоид |
|||||||||
пересекает по 2-м прямым y 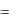 ba x .
ba x .
Цилиндры второго порядка.
В зависимости от характера сечения плоскостью XOY рассматриваемого цилиндра, рассматривают следующие цилиндры:
Гиперболический цилиндр. Каноническое уравнение гиперболического цилиндра имеет вид:
x2 |
|
y 2 |
1 |
a2 |
|
b2 |
|
|
|
Эллиптический цилиндр. Каноническое уравнение эллиптического цилиндра имеет вид:
x2 |
|
y 2 |
1 |
a2 |
|
b2 |
|
|
|
Параболический цилиндр. Каноническое уравнение параболического цилиндра имеет вид:
y 2 2 px
Линейные преобразования и матрицы
С помощью равенств
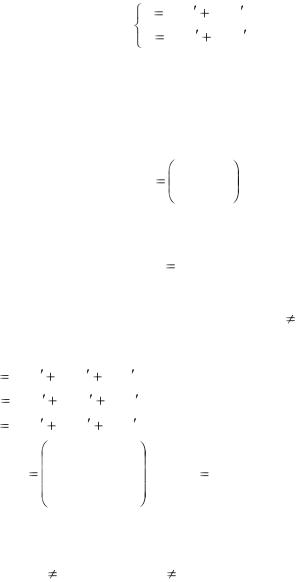
x |
a11 x |
a12 y |
y |
a21 x |
a22 y |
значения переменных x и у можно выразить линейно через значения переменных х' и y'. Эти равенства принято называть линейным преобразованием переменных х' и у'.
Их можно рассматривать также как линейное преобразование координат точки (или вектора) на плоскости. Таблица
A |
a11 |
a12 |
|
a21 |
a22 |
||
|
называется матрицей рассматриваемого линейного преобразования, а определитель
DA |
a11 |
a12 |
|
|
a21 |
a22 |
|
|
|
|
|
|
||
— определителем линейного |
преобразования. |
В |
||
дальнейшем будем предполагать, что DA 0 |
|
|||
Можно также рассматривать линейное преобразование трех переменных (т. е. для пространства)
x |
a11 x |
a12 y |
a13 z |
|
|
|
|
|
|
y a21 x a22 y a23 z , |
|
|
|
|
|
||||
z |
a31 x |
a32 y |
a33 z |
|
|
|
|
|
|
|
|
a11 |
a12 |
a13 |
|
a11 |
a12 |
a13 |
|
|
|
|
|
||||||
где A |
a21 |
a22 |
a23 |
и DA |
a21 |
a22 |
a23 |
|
|
|
|
a31 |
a23 |
a33 |
|
a31 |
a23 |
a33 |
|
|
|||||||||
— соответственно матрица и определитель этого |
|||||||||
преобразования. |
|
|
|
|
|
|
|||
Матрица |
А называется невырожденной (неособой), |
||||||||
если DA |
0 .Если же DA |
0 , то матрица называется |
|||||||
вырожденной (особой). Матрицы
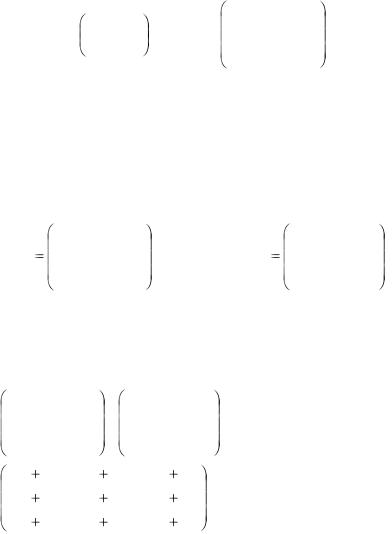
a11 |
a12 |
|
a11 |
a12 |
a13 |
|
и |
a21 |
a22 |
a23 |
|||
a21 |
a22 |
|||||
|
a31 |
a23 |
a33 |
|||
|
|
|
||||
называются квадратными |
матрицами |
соответственно |
||||
второго и третьего порядков. |
|
|
||||
Для большей общности ряд определений будет дан для
матриц |
третьего порядка; |
применение их к матрицам |
второго порядка не вызывает затруднений. |
||
Если элементы квадратной |
матрицы удовлетворяют |
|
условию атп = апт, матрица называется симметрической. Две матрицы
a11 |
a12 |
a13 |
|
|
b11 |
b12 |
b13 |
A a21 |
a22 |
a23 |
и |
B |
b21 |
b22 |
b23 |
a31 |
a23 |
a33 |
|
|
b31 |
b23 |
b33 |
считаются равными (А=В) тогда и только тогда, когда
равны их |
соответственные элементы, т. е. когда атп = bтп |
|||||
(т, п = 1, 2, 3). |
|
|
|
|
||
Суммой двух |
матриц А |
и В |
называется матрица, |
|||
определяемая равенством |
|
|
||||
a11 |
a12 |
a13 |
b11 |
b12 |
b13 |
|
a21 |
a22 |
a23 |
+ b21 |
b22 |
b23 |
= |
a31 |
a23 |
a33 |
b31 |
b23 |
b33 |
|
a11 |
b11 |
a12 |
b12 |
a13 |
b13 |
|
a21 |
b21 |
a22 |
b22 |
a23 |
b23 |
|
a31 |
b31 |
a23 |
b23 |
a33 |
b33 |
|
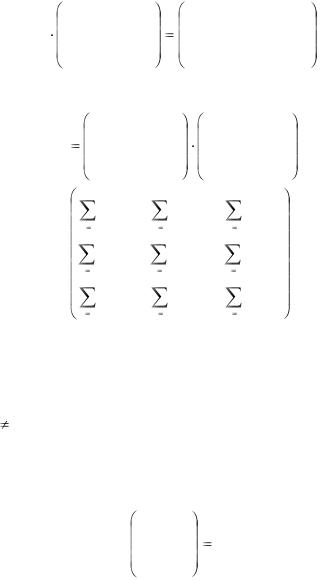
Произведением числа т на матрицу А называется матрица, определяемая равенством
a11 |
a12 |
a13 |
ma11 |
ma12 |
ma13 |
m a21 |
a22 |
a23 |
ma21 |
ma22 |
ma23 |
a31 |
a23 |
a33 |
ma31 |
ma23 |
ma33 |
Произведение двух матриц А и В обозначается символом
АВ и определяется равенством
|
a11 |
a12 |
a13 |
b11 |
b12 |
b13 |
|
AB |
a21 |
a22 |
a23 |
b21 |
b22 |
b23 |
= |
|
a31 |
a23 |
a33 |
b31 |
b23 |
b33 |
|
3 |
3 |
3 |
|||
|
a1 j b j1 |
|
a1 j b j 2 |
|
a1 j b j3 |
j |
1 |
j |
1 |
j |
1 |
3 |
|
3 |
|
3 |
|
= |
a2 j b j1 |
|
a2 j b j 2 |
|
a2 j b j 3 |
j |
1 |
j |
1 |
j |
1 |
3 |
|
3 |
|
3 |
|
|
a3 j b j1 |
|
a3 j b j 2 |
|
a3 j b j 3 |
j |
1 |
j |
1 |
j |
1 |
т. е. элемент матрицы-произведения, стоящий в i-й строке и k-м столбце, равен сумме произведений соответственных элементов i-й строки матрицы А и k-го столбца матрицы В. По отношению к произведению двух матриц переместительный закон, вообще говоря, не выполняется:
AB BA .
Определитель произведения двух матриц равен произведению определителей этих, матриц.
Нулевой матрицей называется матрица, все
элементы которой равны нулю: |
|
||
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Сумма этой матрицы и любой матрицы А дает матрицу А: А+0 = А. Единичной матрицей называется матрица

1 |
0 |
0 |
E 0 |
1 |
0 |
0 |
0 |
1 |
При умножении этой матрицы слева или справа на
матрицу А получается |
матрица AE EA |
A Единичной |
|
матрице. |
отвечает |
тождественное |
линейное |
преобразование: х=х', у=у', z = z'.
Матрица В называется обратной по отношению к матрице А, если произведения АВ и ВА равны единичной матрице: АВ=ВА = Е.
Для матрицы, обратной по отношению к матрице А, принято обозначение А-1, т. е. В = А-1.
Всякая невырожденная квадратная матрица А имеет обратную матрицу. Обратная матрица находится по формуле
|
|
A11 |
|
A21 |
|
A31 |
|
|
DA |
|
DA |
|
DA |
A |
1 |
A12 |
|
A22 |
|
A32 |
|
DA |
|
DA |
|
DA |
|
|
|
|
|
|||
|
|
A13 |
|
A23 |
|
A33 |
|
|
DA |
|
DA |
|
DA |
где Атп- - алгебраическое дополнение элемента матрицы атп в ее определителе, т. е. произведение минора второго порядка, полученного вычеркиванием m-й строки и n-го столбца в определителе матрицы А, на (-1)т+п.
Матрицей-столбцом называется матрица
x1
Xx2 x3
Произведение АХ определяется равенством
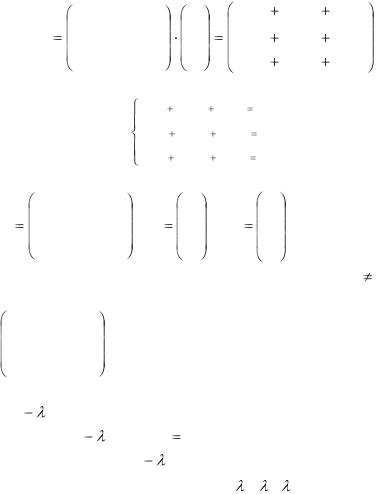
|
a |
a |
a |
x |
a11 x a12 yй |
a13 z3 |
|
|
11 |
12 |
13 |
1 |
|
|
|
AB |
a21 |
a22 |
a23 |
x2 |
a21 x1 |
a22 y2 |
a23 z3 . |
|
a31 |
a23 |
a33 |
x3 |
a31 x1 |
a32 y2 |
a33 z3 |
Система уравнений
a11x1 |
a12 y2 |
a13z3 |
b1 |
a21x1 |
a22 y2 |
a23z3 |
b2 |
a31x1 |
a32 y2 |
a33z3 |
b3 |
может быть записана в виде АХ = В, где
a11 |
a12 |
a13 |
|
x1 |
b1 |
A a21 |
a22 |
a23 |
, X |
x2 |
и В b2 |
a31 |
a23 |
a33 |
|
x3 |
b |
Решение этой системы имеет вид Х = А-1В (если D |
A |
0 ). |
|||||||
|
|
|
|
|
|
|
|
|
|
Характеристическим уравнением матрицы |
|
|
|
||||||
|
a11 |
a12 |
a13 |
|
|
|
|
|
|
|
a21 |
a22 |
a23 |
|
|
|
|
|
|
|
a31 |
a23 |
a33 |
|
|
|
|
|
|
называется уравнение |
|
|
|
|
|
||||
|
a11 |
|
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a21 |
|
a22 |
a23 |
0 |
|
|
|
|
|
a31 |
|
a23 |
a33 |
|
|
|
|
|
Корни |
|
этого |
уравнения |
11 , 2 , 3 |
называются |
||||
характеристическими числами матрицы; они всегда действительны, если исходная матрица является симметрической.
Система уравнений

(a11 |
|
) 1 |
a12 2 |
a13 3 |
0 |
|
a21 |
1 |
(a22 |
) 2 |
a23 3 |
0 , |
|
a31 |
1 |
a32 2 |
(a33 |
) 3 |
0 |
|
в которой |
имеет одно из значений |
1, 2 , 3 и |
||||
определитель, которой в силу этого равен нулю,
определяет тройку чисел |
1 , 2 , 3 |
соответствующую |
данному характеристическому числу. |
|
|
Эта совокупность трех чисел |
1 , 2 , 3 с точностью |
|
до постоянного множителя определяет ненулевой вектор r 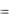 1i
1i 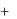 2 j
2 j 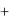 3 k , называемый собственным вектором
3 k , называемый собственным вектором
матрицы.
Линейные пространства.
Основные понятия. Рассмотрим такое множество R элементов x, y, z …, в котором для любых двух элементов
x R и y |
R |
определена сумма |
x y |
R и для любого |
||
элемента |
x |
R и любого |
действительного |
числа |
||
определено |
|
произведение |
x |
R . |
Если |
сложение |
элементов множества R и умножение элемента этого множества на действительное число удовлетворяет следующим условиям:
1.х + у = у + х;
2.( х + у ) + z = х + ( у + z );
3. |
существует такой элемент 0 |
; R (нуль-элемент), что х + |
|
|
0 = х для любого x R ; |
|
|
4. |
для |
каждого элемента x |
R существует элемент |
|
y |
R такой, что х + у = 0 (в дальнейшем будем писать |
|
у= - х, т. е. х + (- х ) = 0);
5.1 x 1;
x 1;

6. |
x |
|
|
x ; |
7. |
( |
)x |
x |
x ; |
8. |
(x |
y) |
x |
y ; |
то множество R называется линейным (или векторным) пространством, а элементы х, у, z, ... этого пространства - векторами.
Например, множество всех геометрических векторов является линейным пространством, так как для элементов этого множества определены действия сложения и умножения на число, удовлетворяющие сформулированным условиям.
Разностью двух векторов х и у линейного пространства называется такой вектор V этого пространства, что у + v = х. Разность векторов х и у
обозначают через х - у, то есть |
х - у = v. Легко |
доказывается, что х – у = х + ( - у). |
|
Справедливы также следующие теоремы: |
|
1.В каждом линейном пространстве существует только один нуль-элемент.
2. |
Для |
каждого |
элемента |
x |
R линейного пространства |
|||
|
существует только один |
противоположный элемент. |
||||||
3. |
Для каждого элемента выполняется равенство 0 x |
0 . |
||||||
4. |
Для |
любого |
действительного |
числа |
и |
|||
|
0 |
R выполняется равенство |
0 |
0 . |
|
|||
5. |
Из равенства |
|
x 0 следует одно из двух равенств: |
|||||
|
|
0 или x |
0 . |
|
|
|
|
|
6. |
Элемент |
1 |
x является |
противоположным |
для |
|||
|
элемента х. |
|
|
|
|
|
|
|
Линейно независимые векторы.
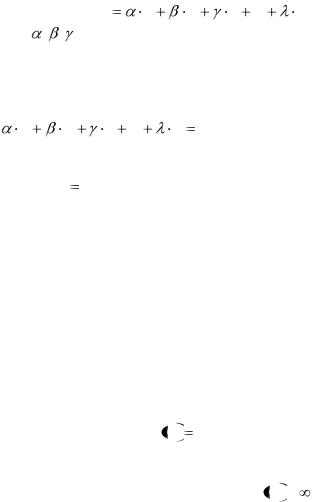
Пусть х, у, z, .., u. - какие-нибудь векторы линейного пространства R. Вектор, определяемый равенством
v |
x |
y |
z ... |
u |
где , , ,..., 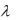 действительные числа, также принадлежат
действительные числа, также принадлежат
линейному пространству R. Этот вектор называется линейной комбинацией векторов х, у, z, ..,u . Пусть линейная комбинация векторов х, у, z, ..,u является нуль - вектором, т. е.
x |
y |
z ... |
u 0 |
(*) |
|
Векторы |
х, у, |
z, |
..,u называются линейно |
независимыми, если равенство (*) выполняется лишь при
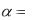
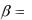
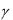 ...
... 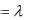 . Если же равенство (*) может выполняться и в том случае, когда не все числа
. Если же равенство (*) может выполняться и в том случае, когда не все числа 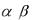
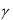
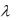
равны нулю, то говорят, что векторы х, у, z, ..,u линейно зависимы.
Легко доказывается, что векторы х, у, z, ..,u линейно зависимы тогда и только тогда, когда один из этих векторов может быть представлен в виде линейной комбинации остальных векторов.
3. Размерность и базис линейного пространства. Если в линейном пространстве R имеется n линейно независимых векторов, но любые n + 1 векторов этого пространства линейно зависимы, то пространство R называют n-мерным. Принято также говорить, что размерность пространства R равна n, и писать d R n . Пространство, в котором
можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным. Если R - бесконечномерное пространство, то d R 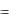 .
.
Совокупность n линейно независимых векторов n- мерного линейного пространства называется базисом. Справедлива следующая теорема: каждый вектор линейного n-мерного пространства может быть единственным образом представлен в виде линейной
