
Методическое пособие 457
.pdf
комбинации векторов базиса. Так, |
если e1 , e2 ,...en базис n- |
мерного линейного пространства |
R, то любой вектор |
x R может быть единственным |
образом представлен в |
виде
x 1e1 |
2 e2 ... |
n en . |
|
Таким образом, вектор х в базисе |
e1 , e2 ,...en |
определяется |
|
единственным образом с помощью чисел |
1 , 2 ,... n Эта |
||
числа называются координатами вектора х в данном базисе.
Преобразование координат при переходе к новому базису.
Пусть в n-мерном линейном пространстве R0 имеются два
базиса: e1 , e2 ,...en (старый) и e1 , e2 ,...en (новый). Даны зависимости, выражающие каждый вектор нового базиса через векторы старого базиса:
e1 |
|
a11e1 |
a21e2 |
... an1en , |
|
e2 |
|
a12 e1 |
a22 e2 |
... an 2 en , |
|
.......... .......... .......... .......... ....... |
|||||
en |
|
a1n e1 |
a2n e2 |
... |
ann en , |
Матрицу |
|
|
|
|
|
|
|
a11 |
a12 |
... |
a1n |
|
A |
a21 |
a22 |
... |
a2n |
|
.... ... ... .... |
||||
|
|
||||
|
|
an1 |
an 2 |
... |
ann |

называют матрицей перехода от старого базиса к новому.
Возьмем какой-нибудь вектор х. Пусть |
( 1 , 2 ,... |
n ) - |
координаты этого вектора в старом |
базисе, |
а |
( 1 , 2
, 2 ,... n
,... n ) его координаты в новом базисе. При этом
) его координаты в новом базисе. При этом
старые координаты вектора х выражаются через новые координаты этого вектора по формулам
1 |
a11 |
1 |
a12 |
2 |
.... |
a1n |
n |
2 |
a21 |
1 |
a22 |
2 |
.... |
a2n |
n |
.......... .......... .......... .......... .......... ..
n an1 1 an 2 2 .... ann n
которые называются формулами преобразования координат.
Нетрудно видеть, что столбцы матрицы А являются координатами в формулах перехода от старого базиса к новому, а строки этой матрицы—координатами в формулах преобразования старых координат через новые.
Подпространства, образованные решениями однородной линейной системы уравнений.
Рассмотрим однородную линейную систему уравнений
а11 х1 |
а12 х2 |
а13 х3 |
0 |
|
|
а21 |
х1 |
а22 х2 |
а23 х3 |
0 |
(*) |
....... |
|
|
|
|
|
|
|
|
|
|
|
аn1 |
х1 |
аn 2 х2 |
аnn хn |
0 |
|

Пусть |
x1 |
1 , x2 |
2 ,...xn |
n какое-нибудь решение |
|||
системы. |
Запишем |
это |
решение |
в виде вектора |
|||
f |
1 , |
2 ,..., |
n . |
|
|
|
|
Совокупность |
линейно |
независимых |
решений |
||||
f1 , f 2 ,..., |
f n системы |
уравнений |
(*) |
называется |
|||
фундаментальной системой решений, если любое решение системы уравнений (*) может быть представлено в виде линейной комбинации векторов f1 , f 2 ,..., f n
Теорема о существовании и фундаментальной системы решении. Если ранг матрицы
a11 |
a12 |
... |
a1n |
a21 |
a22 |
... |
a2n |
.... |
... ... .... |
||
am1 |
am2 |
... |
amn |
меньше n, то система (*) имеет ненулевые решения. Число векторов, определяющих фундаментальную систему
решении, находится по формуле |
k n r , |
где n - ранг |
|
матрицы. |
|
|
|
Таким образом, если рассматривается линейное |
|||
пространство |
R n векторами |
которого |
являются |
всевозможные системы n действительных чисел, то совокупность всех решений системы (*) является
подпространством пространства R n . Размерность этого подпространства равна k.
Линейные Преобразования
1. Основные понятия. Будем говорить, что в линейном пространстве R задано преобразование А, если каждому
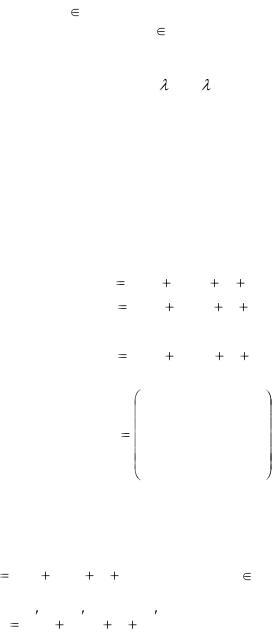
вектору x R по |
некоторому правилу поставлен в |
соответствие вектор |
Ax R Преобразование А называется |
линейным, если для любых векторов х и у и для любого действительного числа А, выполняются равенства
А ( х + у ) = А х + А у, А ( х)= Ах.
Линейное преобразование называется тождественным, если оно преобразует любой вектор х в самого себя. Тождественное линейное преобразование обозначается через Е. Таким образом, Ех = х.
2. Матрица линейного преобразования. Пусть в n-мерном линейном пространстве R, базис которого e1 , e2 ,...en ,
задано линейное преобразование А. Так как Ae1 , Ae2 ,...Aen
векторы пространства R, то каждый из них можно разложить единственным способом по векторам базиса:
Ae1 |
a11e1 |
a21e2 |
... an1en , |
||
Ae2 |
a12 e1 |
a22 e2 |
... an2 en , |
||
.......... .......... .......... .......... ....... |
|||||
Aen |
a1n e1 |
a2n e2 |
... |
ann en , |
|
Матрица |
|
|
|
|
|
|
a11 |
a12 |
... |
a1n |
|
A |
a21 |
a22 |
... |
a2n |
|
.... ... ... .... |
|||||
|
|||||
|
am1 |
am 2 |
... |
amn |
|
называется матрицей линейного преобразования А в базисе e1 , e2 ,...en . Столбцы этой матрицы составлены из
коэффициентов в формулах преобразования базисных векторов. Возьмем в пространстве R какой-нибудь вектор
x |
x1e1 |
x2 e2 ... |
xn en |
Так как Ax R , то и вектор Ах |
можно разложить по векторам базиса: |
||||
Ax |
x1 e1 |
x2 e2 |
... xn |
en |

Координаты x1 , x2 |
,...xn |
|
вектора Ах выражаются через |
|
координаты x1 , x2 ,..., xn |
вектора х по формулам |
|||
x1 |
а11 х1 |
а12 х2 |
а13 хn |
|
x2 |
а21 |
х1 |
а22 х2 |
а23 хn |
....... |
|
|
|
|
xn |
аn1 |
х1 |
аn2 х2 |
аnn хn |
Эти n равенств можно назвать линейным преобразованием А в базисе e1 , e2 ,...en Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А.
Изменение матрицы оператора при переходе от одного ортонормированного базиса к другому.
|
Пусть в одном пространстве задано 2 |
||||
ортонормированных базиса e |
e1 , e2 , e3 и e |
e1 , e2 , e3 . |
|||
|
А – матрица оператора в старом базисе |
|
|||
|
А| - матрица оператора в новом базисе. |
|
|||
Тогда y = A x – оператор А переводит x в y |
|
||||
|
y| = A| x| – оператор A| переводит x| в y|. |
|
|||
y |
Tx |
- связь между |
координатами |
в старом и |
|
y |
Tx |
||||
|
|
|
|||
новом базисах соответственно. Тогда получим следующее соотношение Ty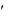 ATX
ATX 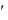 . Получим y в чистом виде. Для этого умножим слева обе части равенства на Т-1.
. Получим y в чистом виде. Для этого умножим слева обе части равенства на Т-1.
T 1T y T 1 ATX
E

y T 1 ATX
T 1 ATX 
Сравним полученное выражение с выражением для оператора в новом базисе:
A X  T 1 ATX
T 1 ATX  или
или
A T 1 AT
T 1 AT
Найдем А через A . Умножим слева на Т, а справа на Т-1 и получим А ТА Т 1 , где Т – матрица перехода от старого базиса к новому.
Действия над линейными преобразованиями.
В приведенных ниже определениях примем следующие обозначения: А и В — произвольные линейные преобразования в линейном пространстве R, — произвольное действительное число, x R любой элемент.
1.Суммой линейных преобразований А и В называется
преобразование С1, определяемое равенством С1х=Ах+Вх. Обозначение: С1=А+В.
2.Произведением линейного преобразования А на число
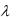 называется преобразование С2, определяемое
называется преобразование С2, определяемое
равенством С2х= Ах. Обозначение. С2= А.
3.Произведением линейного преобразования А на линейное преобразование В называется преобразование
С3, определяемое равенством Сзх=АВх. Обозначение:
Сз=АВ.
4.Преобразования С1, С2 и С3 являются линейными. Матрицы линейных преобразований С1, С2 и С3
определяются из равенств С1=А+В., С2= А., Сз=АВ.
5.При сложении линейных преобразований выполняется переместительный закон: произведение же АВ, вообще говоря, отличается от произведения ВА.

Перечислим некоторые свойства операций над линейными преобразованиями в пространстве R:
A, B C A B,C , AE EA A , A B C AC BC ,
C A B CA CB .
Если для линейного преобразования А найдутся такие линейные преобразования В и С, что ВА=Е, АС=Е, то В=С.
В этом случае |
обозначают |
В=С=А-1, а линейное |
преобразование |
А-1 называют обратным линейным пре- |
|
образованием по отношению к линейному преобразованию
А. Таким образом, |
А-1 А = А А-1 = Е. |
|
|||
Линейное |
преобразование А |
в конечномерном |
|||
пространстве |
называют |
невырожденным, |
если |
||
определитель матрицы этого преобразования отличен от нуля. Следует иметь в виду, что каждое невырожденное
линейное |
преобразование |
А |
имеет |
обратное |
|||
преобразование А-1 и притом только одно. |
|
||||||
Если невырожденное линейное преобразование А в |
|||||||
координатной форме определяется равенствами |
|
||||||
|
x1 |
а11 х1 |
а12 х2 |
а13 хn |
|
||
|
x2 |
а21 |
х1 |
а22 х2 |
а23 хn |
|
|
|
....... |
|
|
|
|
|
|
|
xn |
аn1 |
х1 |
аn2 х2 |
аnn хn |
|
|
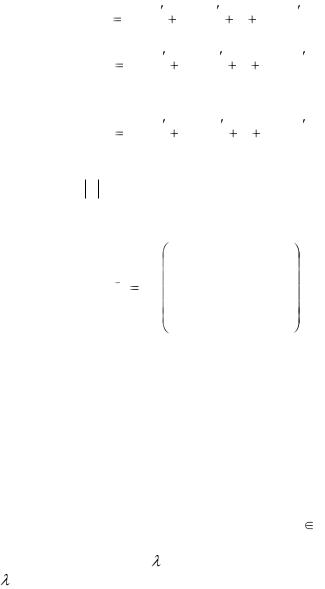
то обратное линейное преобразование А-1 имеет вид
x |
|
|
A11 |
|
x |
A21 |
x |
|
|
... |
An1 |
x |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
n |
|
||||||||
1 |
|
|
A |
1 |
|
|
A |
|
|
|
|
|
A |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
|
|
|
A12 |
|
x |
|
|
A22 |
x |
|
... |
|
An2 |
|
x |
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
n |
|||||||
|
|
|
A |
1 |
|
|
A |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.......... .......... .......... .......... .......... ......
x |
|
|
A1n |
x |
A2n |
x |
|
... |
Ann |
|
x |
|
||||
n |
|
|
|
|
|
|
2 |
|
|
n |
||||||
|
|
A |
1 |
|
A |
|
|
|
|
A |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь АIJ—алгебраическое дополнение элемента аij матрицы А, A определитель матрицы А.
Матрица линейного преобразования А-1 является обратной по отношению к матрице А и определяется равенством
|
|
|
|
А11 |
А12 |
... |
А1n |
|
|
1 |
|
А |
А |
... |
А |
A 1 |
|
|
|
21 |
22 |
|
2n |
|
|
... ... ... ... |
|||||
|
|
A |
|||||
|
|
|
|
Аn1 |
Аn2 |
... |
Аnn |
Характеристические числа и собственные векторы линейного преобразования.
Пусть |
R—заданное |
n-мерное |
линейное |
|
пространство. |
Ненулевой |
вектор |
b |
R называется |
собственным вектором линейного преобразования А, если найдется такое число , что выполняется равенство Аb = b. Само число 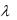 называется характеристическим числом линейного преобразования А, соответствующим вектору b.
называется характеристическим числом линейного преобразования А, соответствующим вектору b.
Перенесем правую часть налево, получим:
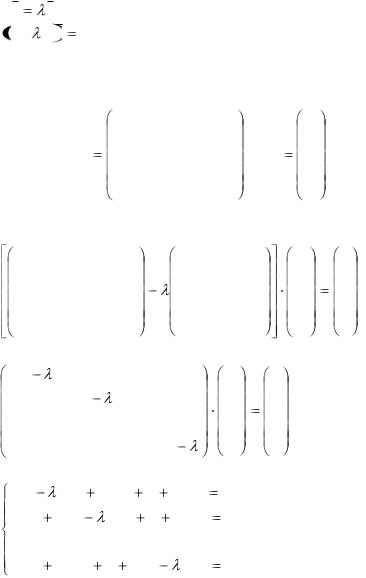
Ab b или A 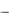 E b 0 .
E b 0 .
Распишем полученное равенство покоординатно. Если линейное преобразование А в базисе e1 , e2 ,...en имеет матрицу
|
|
|
|
А11 |
А12 ... |
|
А1n |
|
|
|
|
b1 |
|
||
|
|
|
А21 |
А22 ... |
|
А2n |
|
|
|
|
b2 |
|
|||
|
|
A |
|
, а |
b |
|
|||||||||
|
|
|
|
... |
... ... ... |
|
|
|
|
... |
|
||||
|
|
|
|
Аn1 |
Аn 2 ... |
|
Аnn |
|
|
|
|
bn |
|
||
то получим следующее матричное уравнение: |
|
||||||||||||||
|
А11 |
А12 ... |
А1n |
|
1 |
|
0 |
... |
0 |
|
|
|
b1 |
0 |
|
|
А21 |
А22 ... |
А2n |
|
0 |
|
1 |
... |
0 |
|
|
|
b2 |
0 |
|
... |
... ... ... |
|
... ... ... ... |
|
|
|
... |
... . |
|||||||
|
Аn1 |
Аn 2 |
... Аnn |
|
0 |
|
0 |
... |
1 |
|
|
|
bn |
0 |
|
Преобразуя, получим |
|
|
|
|
|
|
|
|
|
|
|
||||
|
a11 |
|
a12 |
... |
|
a1n |
|
|
b1 |
|
0 |
|
|
||
|
|
|
|
|
|
|
|
||||||||
|
a21 |
a22 |
... |
|
a2n |
|
|
b2 |
|
0 |
|
|
|||
|
... |
|
... |
... |
|
... |
|
|
... |
|
... . |
|
|||
|
an1 |
an2 |
... |
ann |
|
|
bn |
|
0 |
|
|
||||
Перепишем в виде системы однородных уравнений |
|||||||||||||||
|
(a11 |
k )b1 |
a12b2 |
... a1n bn |
|
0 |
|
|
|
|
|
|
|||
|
a21b1 |
(a22 |
|
k )b2 |
... |
a2n bn |
0 |
|
|
|
|
|
(*) |
||
.......... .......... .......... .......... .......... ....... |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
|
an1b1 |
an 2b2 |
... (ann |
k )bn |
0 |
|
|
|
|
|
|
||||
Система (*) однородная; Нас интересуют ненулевые решения, следовательно, для того, чтобы система имела
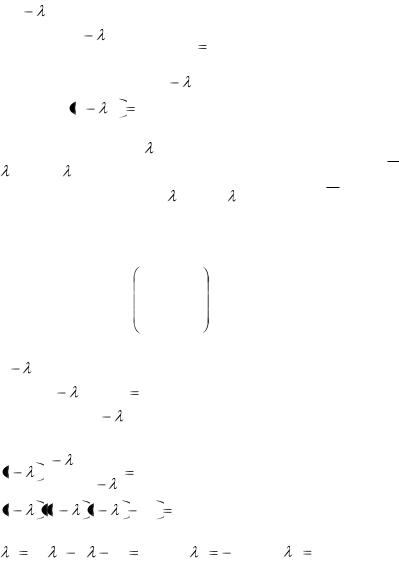
ненулевое решение нужно, чтобы определитель системы равнялся нулю
a11 |
a12 |
... |
a1n |
|
|
a21 |
a22 |
... |
a2n |
0 . |
|
... |
... |
... |
... |
||
|
|||||
an1 |
an 2 |
... |
ann |
|
det A E |
0 . |
Это |
уравнение |
называется |
|
характеристическим |
и |
служит |
для |
нахождения |
|
собственных чисел . В системе (*) подставим вместо число 1 и находим один из собственных векторов b1 .
Затем полагаем вместо число 2 и находим b2 - второй
собственный вектор., соответствующий второму собственному числу и так далее.
Пример. Найти собственные числа и собственные
|
|
|
|
|
|
|
|
1 |
8 |
23 |
|
|
|
векторы оператора |
0 |
5 |
7 . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
3 |
1 |
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
||||
|
|
8 |
|
23 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
5 |
|
7 |
|
|
0 |
|
|
|
|
|
|
0 |
|
3 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
7 |
|
|
0 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||
|
3 |
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
5 |
|
1 |
|
|
21 |
|
0 |
|
|
|
|
|
|
1 |
2 |
6 |
16 |
0 |
|
|
2 |
|
8 . |
||
1 |
|
|
2 |
3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
