
Методическое пособие 457
.pdf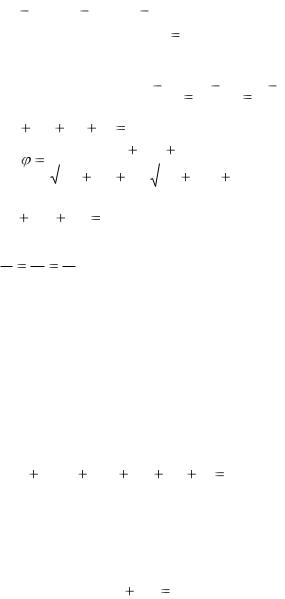
|
x2 |
x1 |
y |
y1 |
z2 |
|
|
|
z1 |
|
|
|
|
|
|
|
|
|
|
||
|
l1 |
|
|
m1 |
|
|
n1 |
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
l2 |
|
|
m2 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||
Угол между прямой |
|
x |
|
|
x1 |
|
|
y |
|
y1 z z1 |
и плоскостью |
||||||||||
|
|
|
l |
|
|
|
m |
|
|
|
n |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Ax |
By |
Cz |
D |
0 определяется по формуле |
||||||||||||||||
sin |
|
|
|
Al |
|
Bm |
Cn |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
A2 |
B2 |
C 2 |
|
l 2 |
|
m |
2 |
n 2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
||||||
условие параллельности прямой и плоскости:
условие перпендикулярности прямой и плоскости:
A B C
l m n
Кривые второго порядка на плоскости.
Канонические уравнения кривых второго порядка.
Общее уравнение кривых второго порядка имеет
вид: |
|
Ax 2 2Bxy Cy 2 Dx Ey F 0 , |
(1) |
|
|
группа старших
где A,B,C,D,E,F – const.
В зависимости от коэффициентов можно получить следующие виды кривых и их вырождения:
1. Эллипс |
x2 |
|
y 2 |
1 |
a2 |
|
b2 |
||
|
|
|
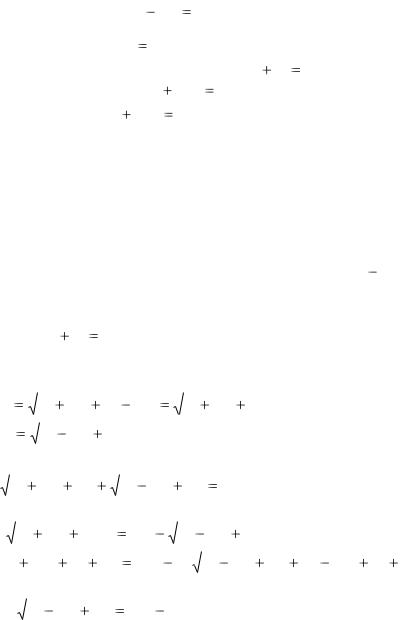
2. |
Гипербола |
x2 |
|
y 2 |
1 |
|
|
|
a2 |
b2 |
|
|
|||||
|
|
|
|
|
||||
3. |
Парабола y 2 |
|
2 px |
|
|
|
||
4. |
Две параллельные прямые Ax2 D 0 , |
D<0 |
||||||
5. |
Две прямые Ax 2 |
Cy 2 |
0 , А и С – разного знака |
|||||
6. |
Точка Ax 2 |
|
Cy 2 |
|
0 , |
А и С – одного знака |
||
Канонические уравнения эллипса,
гиперболы и параболы. Эллипс
Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек F1 ( c,0)
и F2 (c,0) называющимися фокусами – |
есть |
величина |
|||||||||||||||||||||
постоянная, равная 2А. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
r1 |
r2 |
|
2a , где r-фокальный радиус. |
|
(2) |
|||||||||||||
|
|
|
|
|
Чтобы получить уравнение эллипса нужно выразить |
||||||||||||||||||
r1 |
и r2 через координаты x, y. |
|
|
|
|
|
|
||||||||||||||||
r |
|
|
(x c)2 |
|
( y 0)2 |
|
|
|
(x c)2 |
y 2 |
|
|
|
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
(x |
c)2 |
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим r1 |
и r2 |
|
в уравнение (2). |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(x c)2 |
y 2 |
|
|
|
(x c)2 |
|
|
y 2 2a |
|
|
|
|
|
|
||||||||
Упростим это уравнение: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
( (x c)2 |
y 2 )2 |
|
(2a |
|
(x c)2 |
y 2 )2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x2 |
|
2xc c2 |
|
y 2 |
|
4a2 |
4a (x c)2 y 2 |
x2 |
2xc c2 y 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4a (x c)2 |
y 2 |
|
4a2 4xc |
|
|
|
|
|
|
||||||||||||||
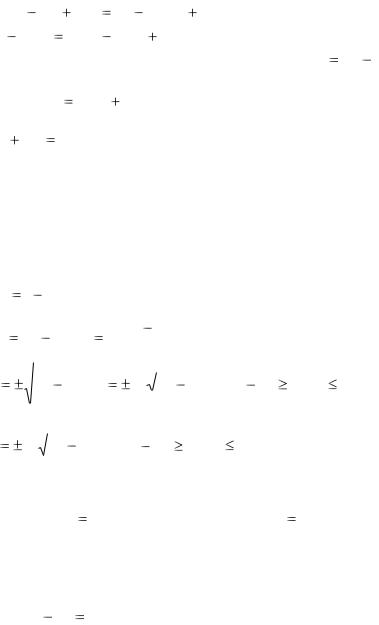
a 2 ((x c)2 |
|
y 2 ) a 4 2a 2 xc x 2 c 2 |
|
|
|||||||
a 4 |
a 2 c 2 |
|
a 2 x 2 |
x 2 c 2 |
a 2 y 2 |
|
|
||||
Пусть |
|
|
|
|
|
b2 |
a2 c2 , |
||||
(3) |
|
|
|
|
|
|
|
|
|
|
|
тогда a 2b2 |
x 2b2 |
a 2 y 2 |
|
: a 2b2 |
|
|
|||||
|
|
|
|||||||||
|
x2 |
|
y 2 |
|
1 |
- |
каноническое |
уравнение |
эллипса. |
||
|
a2 |
|
b2 |
||||||||
|
|
|
|
|
|
|
|
|
|||
(4) |
|
|
|
|
|
|
|
|
|
|
|
Исследуем форму эллипса.
Уравнение эллипса содержит члены только с четными степенями текущих координат. Поэтому определенная им линия симметрична относительно Ox и Oy.
Выразим из (4) у как функцию от x.
|
y 2 |
1 |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
b2 |
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y 2 |
b2 |
b2 |
x2 |
b2 a2 |
b2 x2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
a2 |
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
b2 |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y |
|
|
b2 |
|
x2 |
|
a 2 |
x2 , a2 x2 0 , |
|
x |
|
a |
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a 2 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Аналогично выразим из (4) х, как функцию от у. |
||||||||||||||||||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
b 2 |
y 2 |
|
|
|
|
|
|
|
|
|
|
||
|
x |
|
|
|
|
b2 |
|
|
y 2 , |
0 , |
|
y |
|
b |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
a |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точки, в которых эллипс пересекает оси называются его вершинами ( A1 A2 , B1 B2 ) . Осями эллипса называются отрезки A1 A2 2a - большая полуось, B1 B2 2b - малая
полуось. Если фокусы эллипса расположены на оси абсцисс a>b. Если фокусы эллипса расположены на Oy (b>a), тогда уравнение эллипса имеет вид (4), уравнение
(3) имеет иной вид
b2 c2 a2 |
(3’) |

Тогда большой полуосью называют OB1 |
OB2 |
b , а |
|||||
малой полуосью называют OA1 |
OA2 |
a . |
|
||||
|
Эксцентриситетом эллипса называют отношение |
||||||
расстояний между фокусами и длинны его большей оси |
|||||||
|
|
c |
- фокусы на Ох |
|
|
(5) |
|
|
|
a |
|
|
|||
|
|
|
|
|
|
||
|
|
c |
|
- фокусы на Оу |
|
|
(5’) |
|
|
b |
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
0 |
1 |
|
|
|
Эксцентриситет характеризует форму эллипса. Чем |
||||||
ближе |
1, тем сильнее втянут эллипс. Если |
0 , то |
|||||
получается окружность x 2 y 2 |
a 2 |
|
|
||||
Гипербола
Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек фокуса есть величина постоянная (разность берется по модулю), меньшая расстояния между фокусами.
Фокусы гиперболы F1 и F2 . Расстояние между
ними F1 F2 |
2c , F1 ( c,0) , F2 (c,0) . |
|
|
|
||
M (x, y) - |
произвольная |
точка гиперболы. |
F1M |
r1 , |
||
F2 M r2 |
|
|
F2 M |
|
2a |
|
- фокальные |
радиусы. |
F1M |
|
|||
(6) |
|
|
|
|
|
|
2a 2c a c
Выведем уравнение гиперболы: |
|
||||
r1 r2 |
2a |
|
|
|
|
r |
x c 2 y 2 , |
r |
x c 2 |
y 2 |
|
1 |
|
|
2 |
|
|
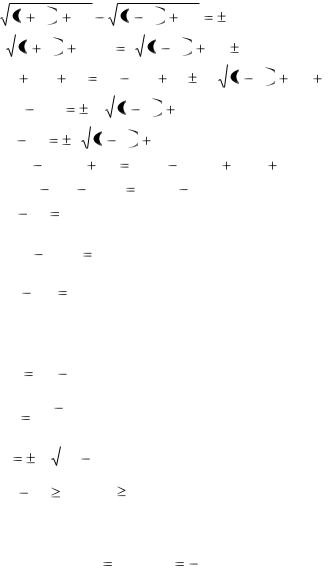
|
|
x c 2 |
y 2 |
x c 2 |
y 2 |
|
2a |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
( x c 2 |
y 2 )2 |
( x c 2 |
y 2 |
|
2a)2 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x 2 |
2cx c 2 |
|
|
|
x 2 |
2cx c 2 |
4a x c 2 |
y 2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4cx 4a 2 |
|
4a x c 2 |
y 2 |
|
|
|
|
|
|||||||||||||||||||||
cx |
a 2 |
a |
|
x |
c 2 |
|
y 2 |
|
|
|
|
|
|
|
|
||||||||||||||
c 2 x 2 |
|
|
2a 2 xc a 4 |
a 2 x 2 |
2a 2 xc a 2 c 2 |
a 2 y 2 |
|||||||||||||||||||||||
|
x 2 (c 2 a 2 ) a 2 y 2 |
a 2 (c 2 |
a 2 ) |
|
|
|
|
||||||||||||||||||||||
c2 |
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(7’) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x 2b2 |
|
|
a 2 y 2 |
|
a 2b2 |
|
|
: a 2b2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x2 |
|
|
y 2 |
|
1 |
- |
|
|
каноническое |
|
уравнение |
|||||||||||||||||
|
a2 |
|
b2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Исследуем уравнение (7): |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
y 2 |
|
|
|
x2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a2 |
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
y 2 |
|
x2 |
a2b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y |
|
|
|
x2 |
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x2 |
a2 |
0 , |
|
|
|
x |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4a 2
гиперболы.
Так как в уравнении (7) только четные степени, поэтому определенная им линия симметрична относительно Ox и
Oy. Прямые y |
b |
x и |
y |
b |
x называются асимптотами |
|
|
||||
|
a |
|
a |
||
гиперболы. |
|
|
|
|
|

Определение: Прямая l называется асимптотой для графика функции y 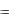 f (x) , если при движении точки М по кривой к бесконечности, расстояние от точки М до прямой
f (x) , если при движении точки М по кривой к бесконечности, расстояние от точки М до прямой
l стремится к бесконечности. |
|
|
|
|
||||||
Точки, в которых гипербола |
пересекает |
ось Ох |
||||||||
A1 ( a,0) и |
A2 (a,0) называются вершинами гиперболы. |
|||||||||
Отрезки A1 A2 2a и |
B1 B2 |
2b |
называются |
осями |
||||||
гиперболы. Точка O(0,0) называется центром гиперболы. |
||||||||||
Уравнение |
вида |
x2 |
|
y 2 |
|
1 |
определяет гиперболу с |
|||
a2 |
b2 |
|||||||||
|
|
|
|
|
|
|||||
фокусами на оси ординат. Эта гипербола называется сопряженной с (7).
Гиперболы с равными полуосями а=b называются
равносторонними. ( x 2 y 2 |
a 2 ) |
|
||
Эксцентриситет |
|
c |
характеризует форму |
|
|
|
|
||
|
a |
|||
|
|
|
||
гиперболы, чем меньше , тем больше вытянут ее основной прямоугольник вдоль действительной оси.
Парабола
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости называется фокусом, а расстояние до некоторой прямой называется директриссой.
|
|
Величину |
p 0 называют параметром. Точка М(х, |
|||||||
у) – произвольная точка. |
r |
MF( p / 2,0) , |
MQ d по |
|||||||
определению |
параболы |
r |
d , |
l – |
директрисса. |
|||||
|
|
|
|
|
|
|
||||
r |
|
(x p / 2)2 |
y 2 , d |
(x p / 2)2 |
|
x p / 2 |
||||
|
|
|
|
|
|
|
|
|
||
|
(x p / 2)2 |
y 2 |
x p / 2 |
|
|
|
|
|
||

x2 |
px |
p2 |
y 2 |
x2 |
px |
p2 |
|
4 |
4 |
||||||
|
|
|
|
|
|||
y 2 |
2 px |
|
|
|
|
|
p 0 - каноническое уравнение параболы, ось которой
совмещена с Ох, она симметрична относительно Ох. – график находится в правой полуплоскости.
Поверхности второго порядка.
Определение: Поверхностью S второго порядка называется геометрическое место точек, декартовые прямоугольные координаты которых удовлетворяют уравнению вида:
a x2 |
a |
22 |
y 2 |
a |
33 |
z 2 |
2a xy 2a xz 2a |
23 |
yz |
|
11 |
|
|
|
|
12 |
13 |
|
|||
2a14 x 2a24 y 2a34 z a44 |
0 |
|
|
|||||||
(1)
где по крайней мере один из коэффициентов при вторых степенях отличен от нуля. Это уравнение называется общим уравнением поверхности второго порядка.
Поверхность второго порядка называется центральной, если система
a11 x0 |
a12 y0 |
a13 z0 |
a14 |
0 |
a21 x0 |
a22 y0 |
a23 z0 |
a24 |
0 |
a31 x0 |
a32 y0 |
a33 z0 |
a34 |
0 |
имеет |
единственное |
решение. Тогда точка O(x0 , y0 , z0 ) |
||
называется центром поверхности второго порядка. Очевидно, что поверхность второго порядка как
геометрический объект не меняется, если от данной системы координат перейти к другой системе.

С помощью преобразования п-ным переносом и поворотом оси уравнение (1) можно привести к виду
a ' x 2 |
a |
22 |
' y 2 |
a |
33 |
' z 2 |
a |
44 |
' 0 |
|
11 |
1 |
|
1 |
|
1 |
|
|
|||
(2) |
|
|
|
|
|
|
|
|
|
|
a11 0 , a22 0 , a33 0
Классификация центральных поверхностей второго порядка.
Если коэффициенты a11 , a22 , a33 |
- одного знака, а |
|||
a44 0 - то поверхность называется эллипсоидом. |
|
|||
Если знак |
коэффициентов |
a11 , |
a22 , |
a33 |
противоположен |
a44 , то поверхность |
называется |
||
вещественным эллипсоидом. В противном случае – мнимым эллипсоидом.
Каноническое уравнение эллипсоида имеет вид:
|
x2 |
|
y 2 |
|
z 2 |
1 |
|
a2 |
b2 |
|
c2 |
||
|
|
|
||||
(1*) |
|
|
|
|
||
Из уравнения (1*) следует, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат – центром симметрии. a, b, c – называются полуосями эллипсоида и представляют собой длины отрезков от начала координатной плоскости до пересечения эллипсоида с осями координат.
Эллипсоид представляет собой ограниченную поверхность. Рассмотрим сечение эллипсоида плоскостями, параллельными XOY.
Каждая из таких плоскостей определяется уравнением z = k = const.
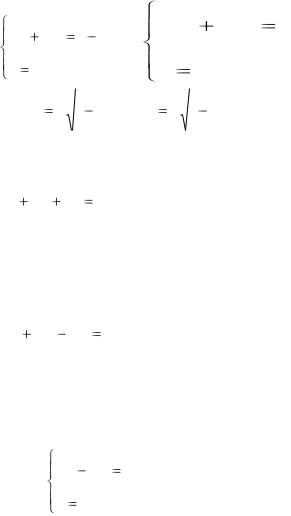
Линия, которая получается в сечении z = h определяется двумя уравнениями.
|
x 2 |
|
y 2 |
|
|
|
h2 |
|
|
x 2 |
|
|
|
|
|
y |
2 |
1 |
||||
|
1 |
|
|
2 |
|
|
|
|
|
b1 |
2 |
|||||||||||
|
a 2 |
b2 |
|
c 2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|||||||||
|
z h |
|
|
|
|
|
|
|
|
|
z |
|
|
|
h |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где a1 |
a 1 |
h2 |
|
, |
b1 b |
1 |
|
h2 |
|
|
|
|||||||||||
c 2 |
|
c2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Аналогичная картина имеет место при рассмотрении сечения, параллельного XOZ, YOZ.
Когда a = b = c = k, эллипсоид является сферой x 2 y 2 z 2 k 2
Если из 4-х коэффициентов a11 , a22 , a33 , a44 два
одного знака, а два другого, то поверхность называется однополосным гиперболоидом. Каноническое уравнение однополосного гиперболоида имеет вид:
x2 |
|
y 2 |
|
z 2 |
1 |
(2*) |
a2 |
|
b2 |
|
c2 |
||
|
|
|
|
Из уравнения (2*) следует, что координатные плоскости являются плоскостями симметрии гиперболоида, а начало координат – центром симметрии.
Рассмотрим сечение плоскостями, параллельными
XOZ (y = 0):
x 2 |
|
z 2 |
1 |
a 2 |
|
c 2 |
|
|
|
||
y |
0 |
|
|
Эта система определяет гиперболоид с полуосями a и c, симметричную относительно координатных осей OX, OY, пересекающую OX в точках (a, 0, 0) и (-a, 0, 0)
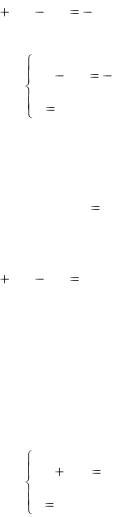
Если знак одного из 3-х коэффициентов a11 , a22 , a33
противоположен знаку остальных, то в этом случае поверхность называется двуполостным гиперболоидом. Каноническое уравнение двуполостного гиперболоида имеет вид:
x2 |
|
y 2 |
|
z 2 |
|
|
1 |
(3*) |
||
a2 |
|
b2 |
c2 |
|
||||||
|
|
|
|
|||||||
|
|
Его сечение координатной плоскостью XOZ: |
|
|||||||
|
|
|
|
x 2 |
|
|
|
z 2 |
1 |
|
|
|
|
|
a 2 |
|
|
|
c 2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
y |
0 |
|
|
|
||
Двуполостный гиперболоид – поверхность, состоящая из 2-х отдельных поверхностей, каждая из которых имеет вид чаши.
Если a44 0 , то поверхность называется конусом
второго порядка. Каноническое уравнение вещественного конуса имеет вид:
x2 |
|
y 2 |
|
z 2 |
0 |
(4*) |
a2 |
|
b2 |
|
c2 |
||
|
|
|
|
Геометрической особенностью является то, что если некоторая точка М лежит на этой поверхности, то все точки прямой, которые проходят через начало координат и точка М, тоже принадлежит конусу. Это вытекает из того, что уравнение (4*) однородно. Такая поверхность называется конической или конусом. Прямые, из которых составлен конус называются образующими. Точка, через которую они проходят называется вершиной.
x 2 |
|
y 2 |
1 |
a 2 |
|
b 2 |
|
|
|
||
z |
l |
|
|
