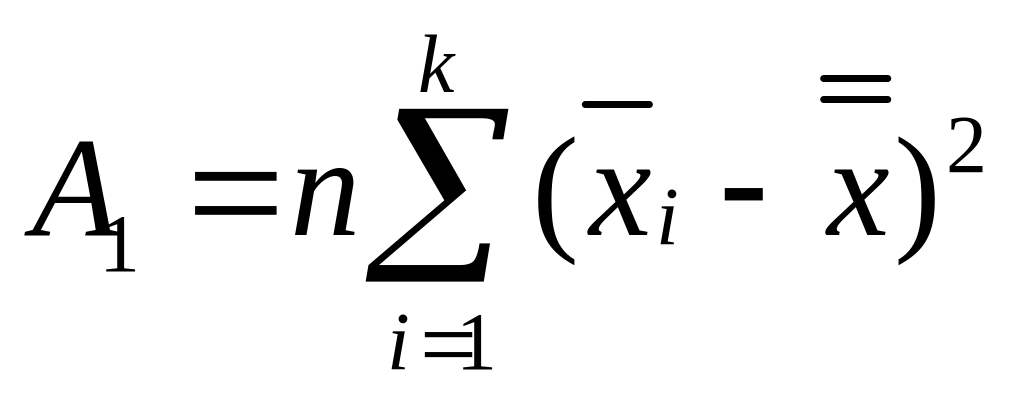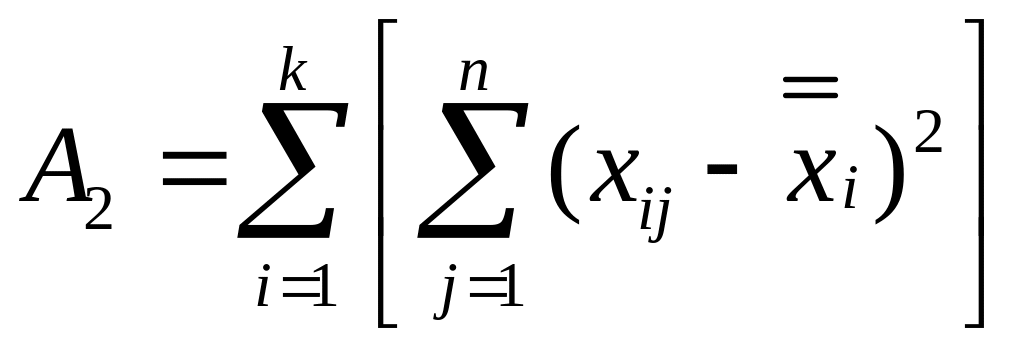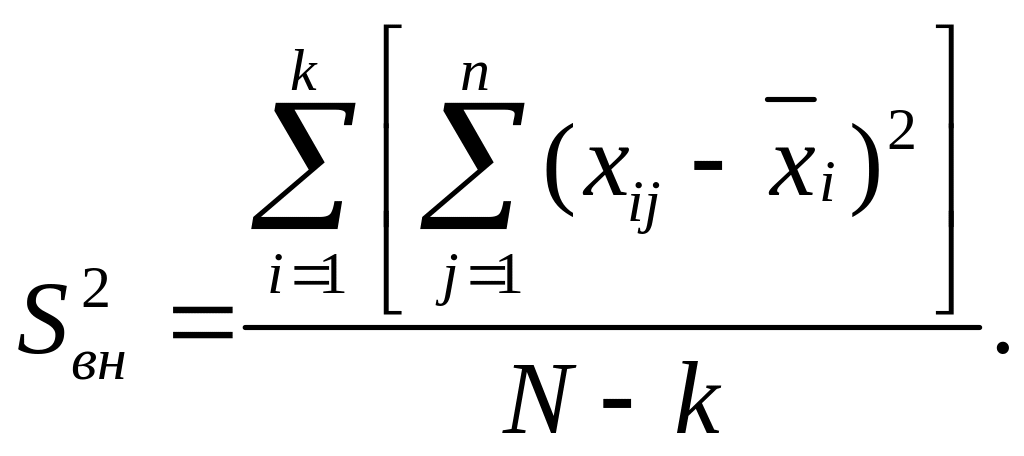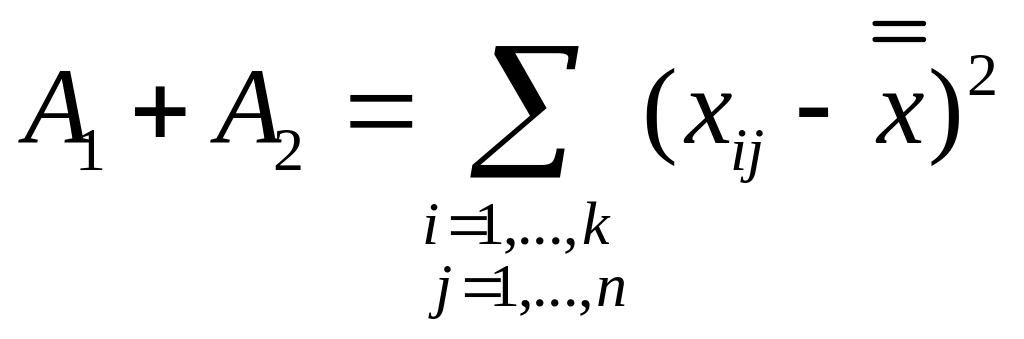- •Математико-статистические методы обработки данных при управлении качеством электронных средств
- •Математико-статистические методы обработки данных при управлении качеством электронных средств Утверждено редакционно-издательским советом
- •Введение
- •1. Общие сведения о контроле качества электронных средств
- •2.2. Графические методы представления статистического ряда
- •2.3. Численные методы представления статистического ряда
- •2.4. Основные понятия теории вероятностей и характеристики генеральной совокупности
- •2.5. Основные законы распределения случайной величины
- •2.6. Статистическая проверка гипотез
- •2.7. Элементы дисперсионного и корреляционного анализа
- •Отклонения толщины фоторезиста от среднего значения при различных частотах вращения центрифуги
- •3. Статистические методы анализа качества. Расслаивание и графические методы
- •3.1. Методы расслаивания
- •3.2. Расслаивание общей изменчивости статистических данных с помощью дисперсионного анализа
- •3.3. Диаграмма разброса (поле корреляции)
- •3.4. Диаграмма Парето
- •3.5. Причинно-следственная диаграмма
- •4. Статистические методы оценки качества
- •4.1. Выбор оценок генеральных характеристик
- •4.2. Определение доверительных интервалов оценок генеральных характеристик
- •4.3. Оценка генеральной средней м(х) с помощью среднего значения выборки
- •Результаты испытаний эс на безотказность работы
- •4.4. Оценка генеральной характеристики рассеивания σ с помощью выборочных характеристик рассеивания
- •4.5. Определение объема выборки для оценки генеральных характеристик с заданной точностью
- •Библиографический список
2.7. Элементы дисперсионного и корреляционного анализа
Дисперсионный анализ. При серийном производстве ЭС часто для обеспечения необходимого объема выпуска осуществляется их одновременное изготовление параллельно на нескольких однотипных технологических линиях. Поэтому, чтобы быть уверенным и получении однородной совокупности ЭС, необходимо ответить на вопрос, является ли работа однотипных линий или технологических установок идентичной. Можно было бы для ответа на этот вопрос применить критерий Стьюдента для попарного сравнения средних арифметических выборок, сделанных из совокупностей ЭС, изготовленных на соответствующих технологических линиях (или установках).
Однако лучшим методом является разложение дисперсий, или дисперсионный анализ. Он основан на том, что при различии в работе технологических линий (или установок) частные средние, вычисленные по выборкам, отличаются друг от друга больше, чем можно было бы ожидать на основе случайных колебаний отдельных значений контролируемого параметра качества.
Пусть имеется k
выборок с одинаковым числом п изделий
в каждой выборке. Тогда число наблюдений
над контролируемым параметром качества
N=kn.
При дисперсионном анализе их располагают
в табл. 2.7 и для каждой выборки наблюдаемых
значений вычисляют частную среднюю
![]() и частную дисперсию si2(i=1,
2,..., k).
и частную дисперсию si2(i=1,
2,..., k).
Общая средняя арифметическая и общая дисперсия, вычисленные по всем наблюдениям, приведенным в табл. 2.7, составляют
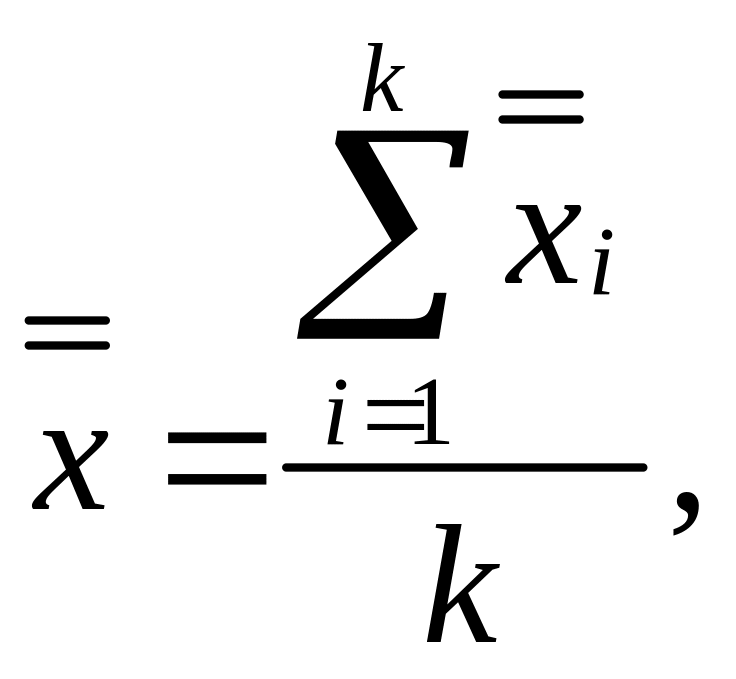 (2.53)
(2.53)
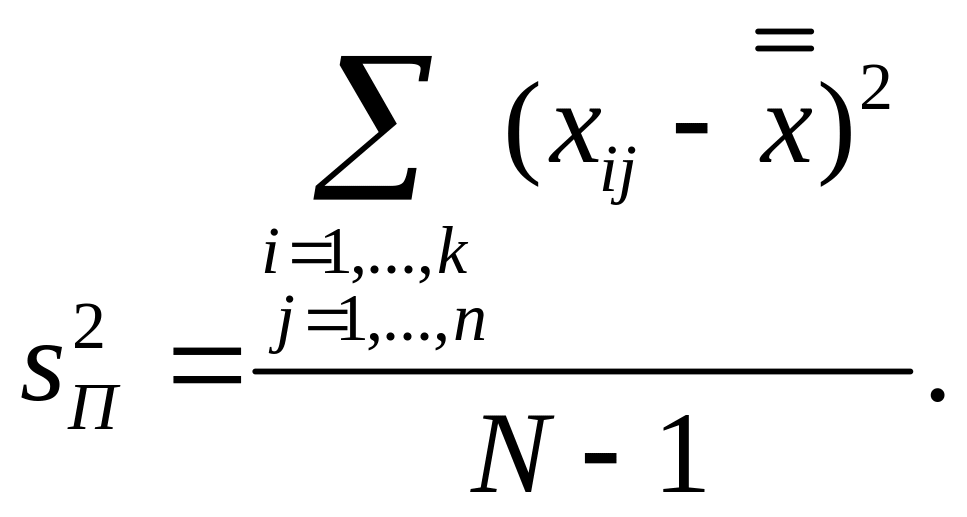 (2.54)
(2.54)
Таблица 2.7
Расположение наблюдаемых значений параметра качества
при дисперсионном анализе
Номер выборки
|
1
|
2
|
3..i.. k
|
Наблюдение xij |
x11 |
x21 |
x31… xi1… xk1 |
. |
x12 |
x22 |
x32… xi2… xk2 |
. |
x13 |
x23 |
x33… xi1… xk3 |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
x1j |
x2j |
x3j… xij… xkj |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
x1n |
x2n |
x3n… xin… xkn |
Частная средняя |
|
|
|
Частная дисперсия |
s12 |
s22 |
s32… si2… sk2 |
Чтобы выборочная дисперсия была несмещенной оценкой генеральной дисперсии, ее получают делением суммы квадратов отклонений случайной величины от их среднего значения не на число наблюдений, а на число степеней свободы. Общая дисперсия sп2 имеет N-1 степеней свободы. Из N наблюдаемых значений N-1 независимы относительно , так как N-1 значений можно выбрать по случайному закону, но после их выбора значение будет определяться значением параметра качества оставшегося изделия.
В дисперсионном анализе кроме общей дисперсии вычисляют еще две другие оценки рассеяния, из которых одна основана на колебании частных средних вокруг общей средней (будем называть ее дисперсией между выборками и обозначать через sср2), а другая — на колебании значений параметра вокруг частной средней внутри отдельных выборок (дисперсия внутри выборок sвн2).
Значение sср2
определяется путем деления изменчивости
между выборками на k
- 1, т. е. на число степеней свободы между
выборками. Из k
значений
можно выбрать по случайному закону
только k-1 значений,
но после их выбора значение будет
определяться средним значением оставшейся
выборки Смысл термина «дисперсия
между выборками» станет понятен, если
вспомнить смысл термина «дисперсия
среднего значения». Предположим, что
сделано k выборок
объемом п и значения
![]() являются средними значениями этих
выборок. Тогда
являются средними значениями этих
выборок. Тогда
![]() можно рассматривать как выборку
объемом k, взятую
из генеральной совокупности всех
возможных средних значений выборок
объемом п. Общая средняя арифметическая
(
)
может быть подсчитана с помощью
(2.53). Следовательно, выражение
можно рассматривать как выборку
объемом k, взятую
из генеральной совокупности всех
возможных средних значений выборок
объемом п. Общая средняя арифметическая
(
)
может быть подсчитана с помощью
(2.53). Следовательно, выражение
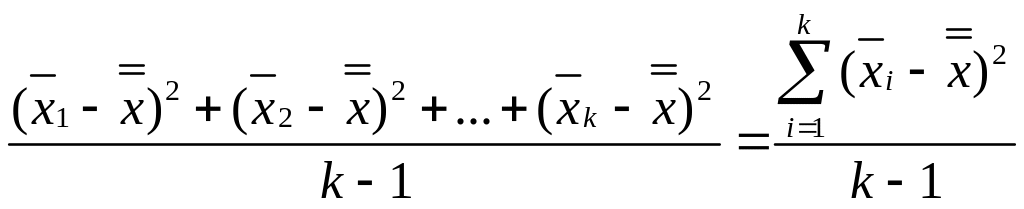
является
наилучшей оценкой
![]() -дисперсии
генеральной совокупности всех
возможных средних значений выборок
объемом п. Но, как известно,
=σ2/n,
а это означает, что выражение
-дисперсии
генеральной совокупности всех
возможных средних значений выборок
объемом п. Но, как известно,
=σ2/n,
а это означает, что выражение
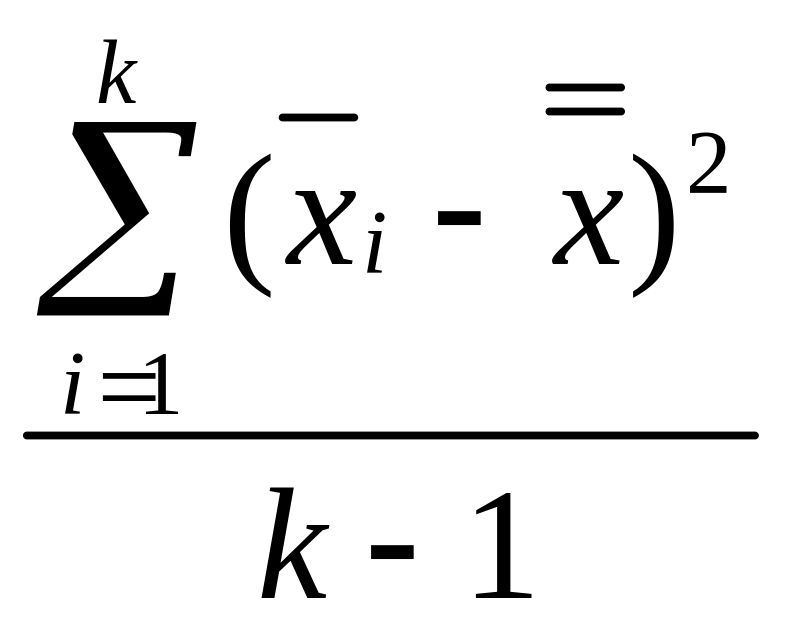 является наилучшей оценкой σ2/п
или
является наилучшей оценкой σ2/п
или
 является наилучшей оценкой σ2.
Поэтому, чтобы дисперсия sср2
была несмещенной оценкой σ 2,
ее следует рассчитывать по формуле
является наилучшей оценкой σ2.
Поэтому, чтобы дисперсия sср2
была несмещенной оценкой σ 2,
ее следует рассчитывать по формуле
 (2.55)
(2.55)
Значение же sвн2 получается делением изменчивости внутри выборок на N—k. Так как для каждой из выборок одна степень свободы оказывается потерянной, а общее число выборок равно k, то v=N—k. Тогда
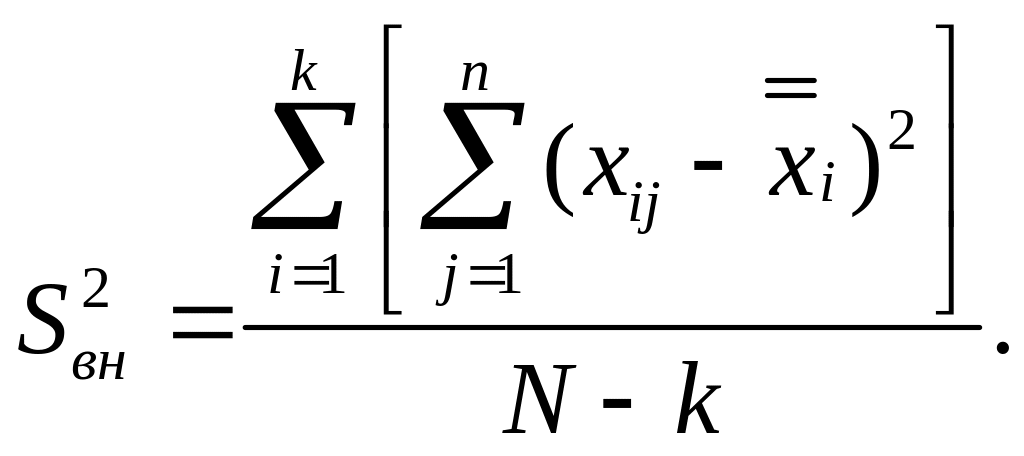 (2.56)
(2.56)
Хотя значения всех рассматриваемых трех оценок могут отличаться друг от друга (для конкретного множества наблюдений), все они являются несмещенными оценками σ -дисперсии генеральной совокупности, из которой взяты выборки.
Схему разложения дисперсии можно представить в виде табл. 2.8.
Таким образом, сумма квадратов отклонений А1 + А2 и общее число степеней свободы N— 1 делятся на две составляющие. Одна составляющая основана на дисперсии частных средних вокруг общего среднего , а другая — на дисперсиях внутри выборок.
Если на выборочные наблюдения не оказывают влияния определенные факторы, то обе оценки дисперсии не отличаются друг от друга. Это можно проверить с помощью F-критерия, а именно F = sср2 / sвн2.
Таблица 2.8
Схема разложения дисперсий
Истонннх дисперсии |
Схема квадратов |
Число степеней свободы |
Дисперсия |
Между выборками |
|
v1 = k-1 |
|
Внутри выборок |
|
v2 = N - k |
|
Общая |
|
v1 – v2= = N - 1 |
|
Пример 5. Рассмотрим влияние частоты вращения центрифуги при нанесении слоя фоторезиста на равномерность слоя фоторезиста. Нанесение слоя фоторезиста осуществляется на установке ПФН-2 на ситаловые подложки, покрытые металлическими пленками. Отклонения толщины пленки фоторезиста (10-6 м) от среднего значения при различных частотах вращения центрифуги приведены в табл. 2.9.
По результатам исследования вычисляем sср2 = 0,0182; sвн2=0,00206; Fрасч = 8,835. Для β=0,05, v1=2, v2=21 по табл. 3 Приложения [3, с. 402] найдем Fтабл = 3,47.
Так как Fрасч>Fтабл, то разброс толщины пленки фоторезиста по подложке зависит от скорости вращения центрифуги.
Таблица 2.9