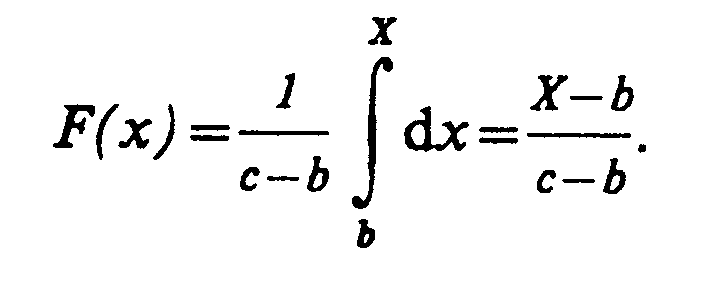2.5. Основные законы распределения случайной величины

В общем случае для определения вероятности того, что случай­ная величина X примет некоторое заранее заданное значение (или окажется меньше его), необходимо знать закон распределения случайной величины. Ввиду того что случайные величины могут быть как дискретными, так и непрерыв­ными, распределения их вероятно­стей будут описываться соответст­венно законами распределения диск­ретных и непрерывных случайных величин.

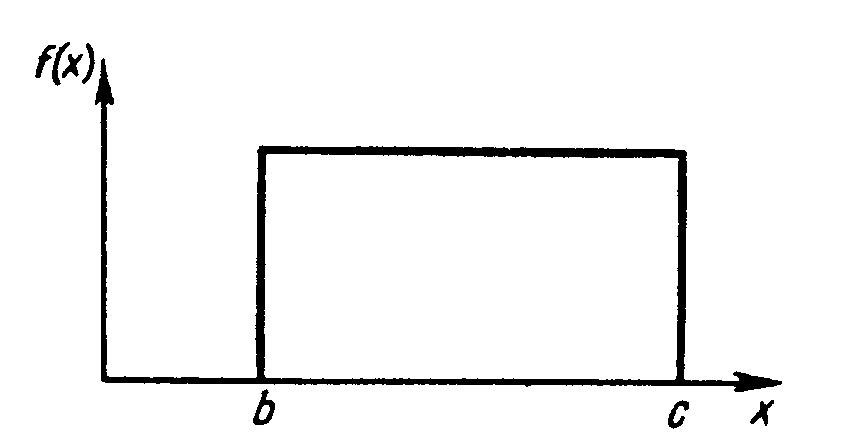
Рис. 2.5. Равновероятное (прямоу­гольное) распределение

Законы распределения для диск­ретных случайных величин, приме­няемые при контроле выпускаемой продукции, подробно рассмотрены в [4], поэтому в данном разделе рассмотрим законы распределения для непрерывных случайных величин, причем только те, которые необходимы для понимания последующего материала.

Равновероятный закон. Простейшим распределением для непре­рывной случайной величины Х является равновероятный (равномер­ный, прямоугольный) закон распределения (рис. 2.5).

Случайная величина X распределена по равновероятному зако­ну, если плотность вероятности

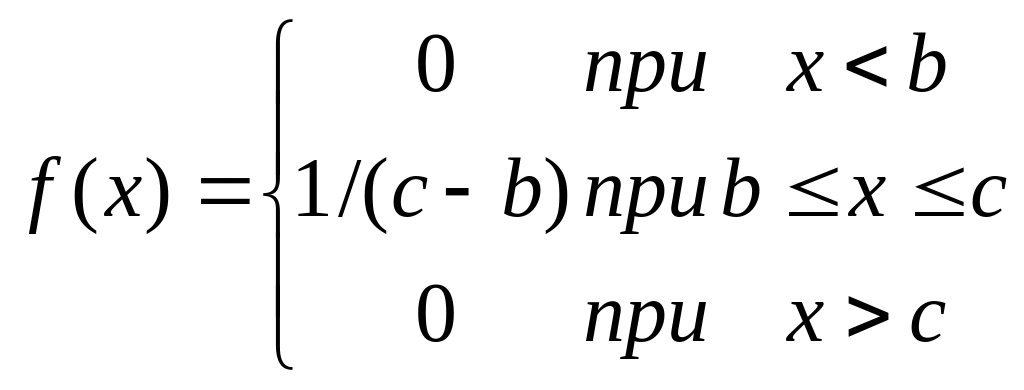(2.24)

Плотность вероятности f(x) иногда называют дифференциальной функцией распределения. Ее физический смысл рассмотрим неско­лько позже. Нетрудно убедиться в том, что площадь под кривой распределения равна единице. Действительно,

(2.25)

Кроме плотности вероятности для непрерывных распределений ис­пользуется также интегральная функция распределения F(x), кото­рая в общем виде выглядит следующим образом:

(2.26)

Для равновероятного закона распределения интегральная функция

(2.27)

Физический смысл интегральной функции распределения состоит в том, что она представляет собой вероятность попадания случай­ной величины х в интервал от -∞ до X, где X — определенное, наперед заданное число.

Гауссовский закон распределения. На практике часто приходится иметь дело с распределениями, которые незначительно отличаются от гауссовского. Широкое распространение гауссовского закона рас­пределения находит теоретическое объяснение в центральной преде­льной теореме, имеющей три условия: случайные величины должны быть независимыми (или слабо зависимыми), их число должно стремиться к бесконечности, среди случайных величин должны отсутствовать превалирующие.

Можно утверждать, что если технологический процесс такого сложного производства, как выпуск современных ЭС, отлажен и ко­нтролируем, то распределение значений параметра качества на каж­дой технологической операции будет близко к гауссовскому. Это можно проверить, набрав достаточную статистику по величинам а и Эк. Особенно часто встречается гауссовский закон при измерени­ях. Такие случайные величины, как ошибки измерений, могут быть представлены как сумма большого числа сравнительно малых сла­гаемых — элементарных ошибок, каждая из которых вызвана дей­ствием отдельной величины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементар­ные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются и сумма оказывается подчиненной закону, близкому к гауссовскому. Основное ограничение, налагае­мое на суммируемые ошибки, состоит в том, чтобы все они в общей сумме равномерно играли относительно малую роль, т. е. должно выполняться третье условие центральной предельной теоремы. Ес­ли это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму слагаемых ошибок резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах ее закон распределения.

Гауссовский закон распределения характеризуется плотностью вероятности

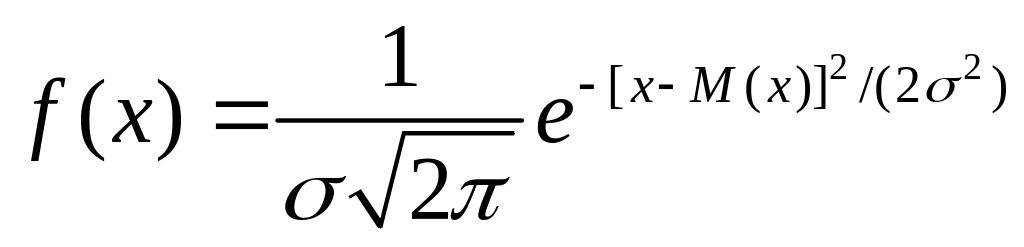(2.28)

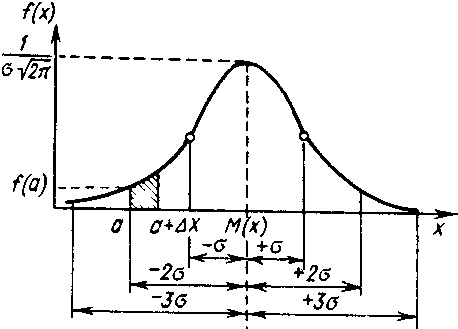
Рис. 2.6. Кривая распределения случайной величины, подчиняющаяся гауссовскому закону

Для определенного распределения М(х) и σ — величины посто­янные. Они являются парамет­рами гауссовского распределе­ния. Графически функция (2.28) представлена на рис. 2.6. Пояс­ним с помощью этого рисунка физический смысл плотности вероятности f(x). Предполо­жим, что случайная величина х представляет собой время ра­боты изделия до отказа (время безотказной работы). Зададим­ся вполне определенным значе­нием времени отказа изделия, равным а, и поставим вопрос следующим образом: какова вероятность того, что данное изделие откажет именно в момент времени x=a? Поставленный таким образом вопрос является некорректным в теории вероятностей. И поэтому ответ будет однозначным: вероятность того, что отказ произойдет в определенный момент времени х = а, равна нулю. Если же вблизи а взять малый интервал, то вероятность того, что случайная величина х попадет в этот интервал,

P[a≤ x ≤ a + ΔX]=f(a) ΔX. (2.29)

При малых ΔХ правая часть уравнения (2.29) представляет собой площадь прямоугольника со сторонами f( а) и ΔХ. Если обе части уравнения (2.29) разделить на ΔХ, то получим вероятность, приходящуюся на единицу длины, т. е. плотность вероятности (аналогично тому, что плотность вещества — это масса на единицу объема)

(2.30)

в этом и заключается физический смысл плотности вероятности.

Вернемся опять к кривой гауссовского закона распределения, приведенной на рис. 2.6. Как видно, кривая распределения имеет характерную колоколообразную форму. Максимальная ордината кривой, равная , соответствует точке х=М(х)—центру распределения. Точка перегиба кривой располагается на расстоянии ±σ от центра распределения (как показано на рис. 2.6). По мере удаления от точки М(х) плотность распределения уменьшается, и при х→±∞ кривая асимптотически приближается к оси абсцисс.

Если при изменении центра группировки М(х) кривая распреде­ления будет смещаться вдоль оси абсцисс, не изменяя своей формы, то при изменении σ кривая распределения меняет свою форму.

Максимальная ордината кривой распределения обратно пропор­циональна σ. Так как площадь под кривой всегда должна оставаться равной единице, то при увеличении σ кривая опускается вниз, одно­временно растягиваясь вдоль оси абсцисс. Напротив, при умень­шении σ кривая вытягивается вверх, одновременно сжимаясь с бо­ков.

Если рассмотреть частный случай, когда М(х) равно нулю, а σ равно единице, то, обозначив плотность вероятности через f₀(x), уравнение (2.28) можно записать в следующем виде:

(2.31)

Функция (2.31) легко табулируется и для нее не представляет труда составить таблицы. С помощью таблицы для f₀ (х) нетрудно вычислить f(x), когда σ не равна единице, а М(х) отлично от нуля. Действительно, из (2.28) и (2.31) имеем

(2.32)

Интегральная функция распределения для случая гауссовского за­кона

(2.33)

С помощью формулы (2.33) определяется вероятность того, что случайная величина х будет меньше некоторого значения X. Если же требуется найти вероятность того, что случайная величина х, име­ющая гауссовский закон распределения, будет лежать в каких-либо пределах от х₁ до х₂, необходимо соответственно изменить пределы интегрирования в выражении (2.33), т. е.

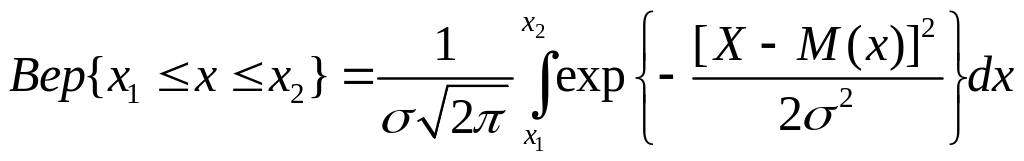(2.34)

Произведя в (2.34) замену переменной интегрирования X на α=[X—M(x)]/σ, которую называют нормированием, и учитывая, что Х= ασ ± М(х), а dx = σdα, получаем

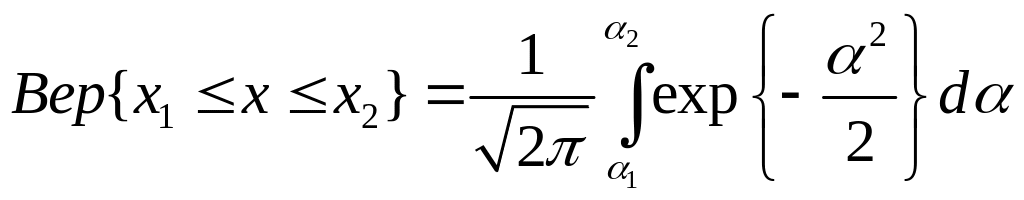(2.35)

Новые нормированные пределы интегрирования α₁ и α₂ заменили пределы х₁ и х₂. Представив правую часть выражения (2.35) в виде суммы двух интегралов, получим

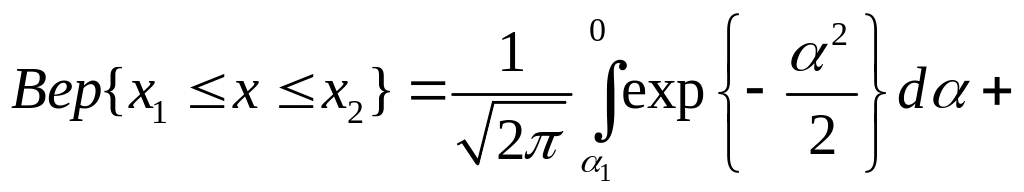
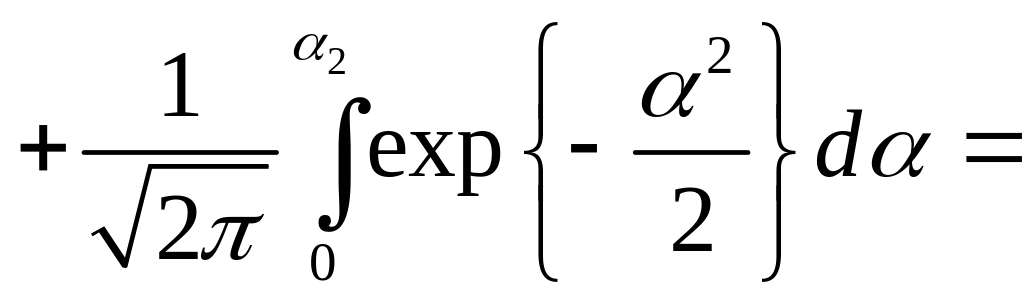
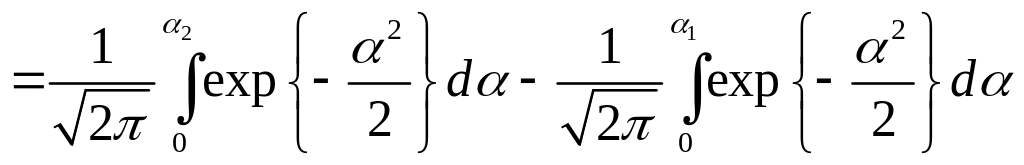
где ;

Знак перед первым слагаемым изменился вследствие изменения пределов интегрирования α₁ - 0 на 0 – α₂.

Функция

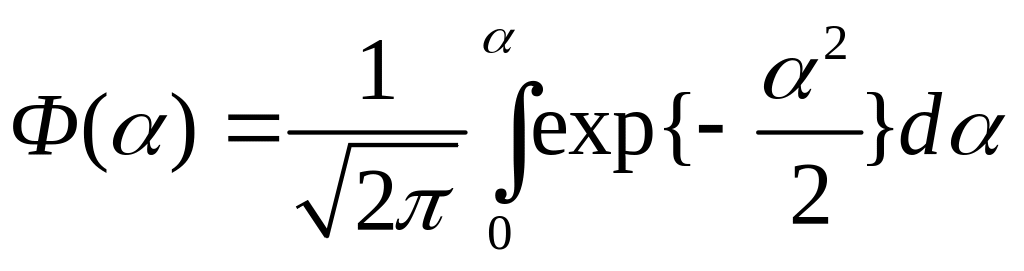(2.36)

называется нормированной функцией Лапласа или интегралом вероятности. Для этой функции имеется в Приложении табл. 1 [3]. Таблица построена для положительных значений, но, учитывая, что функция Ф(α) нечетная, т. е. Ф(-α)=- Ф(α), для отрицательных значений α табличный результат следует брать со знаком минус. В некоторых случаях следует брать функцию

Ф₁(α)=2Ф(α). (2.37)

Таким образом, для получения Ф₁(α) достаточно удвоить значение Ф(α), взятое из табл. 1 Приложения.

Площадь под кривой Гаусса равна 1, или 100% всех значений случайной величины в генеральной совокупности. Величина площади, заключенной между одно-, двух- и трехсигмовыми границами, найденными при подстановке в (2.37) значений Ф(а), взятых из табл. 1 .Приложения [3] для σ, соответственно равного 1, 2 и 3, приведена табл. 2.5.

Таблица 2.5

Величина площади под кривой Гаусса

при различных границах изменения случайной величины

Границы изменения случайной величины X	Площадь под кривой Гаусса
Односигмовые [М(х) — σ; М(х) + σ] Двухсигмовые [М(х) —2σ; М(х) +2σ] Трехсигмовые [М(х) - 3σ; М(х) + 3σ ]	0,6827 0,9545 0,9973

Приведенные в табл. 2.5 данные можно истолковать следующим образом. Если 68,27%, т. е. ²/₃, наблюдаемых значений случайной величины лежит между границами М(х) — σ и М(х) + σ , то 31,73% всех наблюдений следует ожидать за этими границами (соответст­вующими точками перегиба кривой Гаусса), а именно: 15,865% — за границей М(х)— σ; 15,865% — за границей М(х)+ σ в силу симметричности гауссовского распределения. Как уже отмечалось ранее, односигмовые границы соответствуют точкам перегиба кри­вой Гаусса.

Между трехсигмовыми границами [М(х) - 3σ; М(х) + 3σ] нахо­дится 99,73% всех наблюдений, т. е. практически все значения. Только 0,27% значений лежит за этими границами, а именно 0,135% — за границей М (х) -Зσ; 0,135% — за границей М(х) + Зσ. Это означает, что при проведении 10 000 наблюдений в среднем 27 наблюдений будет лежать за трехсигмовыми границами или при 270 наблюдениях — одно. Поэтому, зная стандартное отклонение и математическое ожидание случайной величины, подчиняющейся гауссовскому закону распределения, можно ориентировочно ука­зать интервал ее практически возможных минимальных и макси­мальных значений. И если какое-либо значение появляется за пре­делами трехсигмового участка, то его можно считать чисто случай­ным. Так как вероятность появления такого события очень мала, а именно 1/270, следует считать, что рассматриваемое событие является практически невозможным. Такой способ оценки диапазо­на возможных значений случайной величины известен в математи­ческой статистике под названием правила трех сигм.

На практике участок, лежащий внутри трехсигмовых границ, называют областью статистического допуска параметра качества соответствующего изделия или процесса его изготовления.

Композиция распределений. Пусть имеется целый ряд независимых случайных величин X,, Х₂, Х₃, ... с соответствующими плотностями вероятностей f₁(x),f₂(x), f₃(x), ...,f_n(x). Если составить новую случайную величину Y=X₁+ Х₂+Х₃ + ...+Х_n, то ее распределение будет характеризоваться уже своей плотностью вероятности. Закон распределения величины Y называют композицией (сочетанием) законов рас­пределений величин Х_г, Х₂, Х₃, ..., Х_n. Композиция распределений характеризуется двумя общими свойствами, не зависящими от вида законов распределений.

Первое свойство состоит в том, что математическое ожидание величины У равно арифметической сумме математических ожиданий случайных величин, зако­ны распределений которых составляют композицию распределений:

М (у) =M(x₁) + М(х₂) +М(х₃) + ... + М (х _n). (2.38)

Второе свойство состоит в том, что дисперсия величины Y равна ариф­метической сумме дисперсий случайных величин, законы распределений которых составляют композицию распределений:

σ² (Y)=σ² (x₁)+σ² (x₂) +σ² (x₃)+…+ σ² (x_n) (2-39)

Из этих двух свойств вытекают два интересных следствия:

1. Пусть σ² (x₁)= σ² (x₂) = σ² (x₃)=…= σ² (x_n);

M(x₁) = М(х₂) =М(х₃) = ... = М (х _n) . Тогда σ² (Y) =nσ ²(x); M(Y)=nM(x).

Найдем коэффициент вариации:

V(Y)= σ (y)/M(y) =σ (x)/(√nM(x)). (2.40)

Из выражения (2.40) видно, что с ростом числа наблюдений п коэффициент вариации убывает, а следовательно, точность возрастает пропорционально .

2. Если имеются две (и более) случайные величины, у которых резко отличаются средние квадратические отклонения, то в результате композиции влияние на суммар­ную дисперсию случайной величины, имеющей меньшую дисперсию, практически аннулируется. Действительно, пусть Y=Х₁ +Х₂; σ (х₁) =0,1; σ (х₂) = 1. Тогда, соглас­но второму общему свойству, σ² (у) = σ² (х₁) + σ² (х₂) = 0,01 +1 = 1,01 ≈1 = σ ²(х₂).

Сказанное наглядно подтверждает, что не должно быть сильно отличающихся между собой (превалирующих) независимых случайных величин, для того чтобы в результате композиции их законов распределений получился (в соответствии с третьим условием центральной предельной теоремы) гауссовский закон распреде­ления.

Рассмотрим композицию законов гауссовского и равновероятного распределения.

Если случайная величина X_t распределена по гауссовскому закону (2.28), т. е.

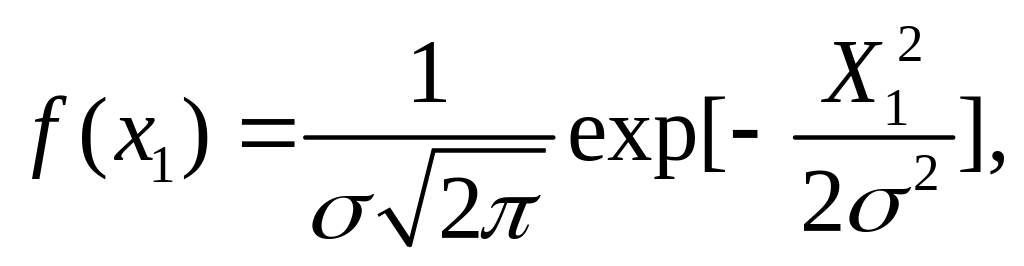
а величина Х₂ следует закону равновероятного распределения (2.24)

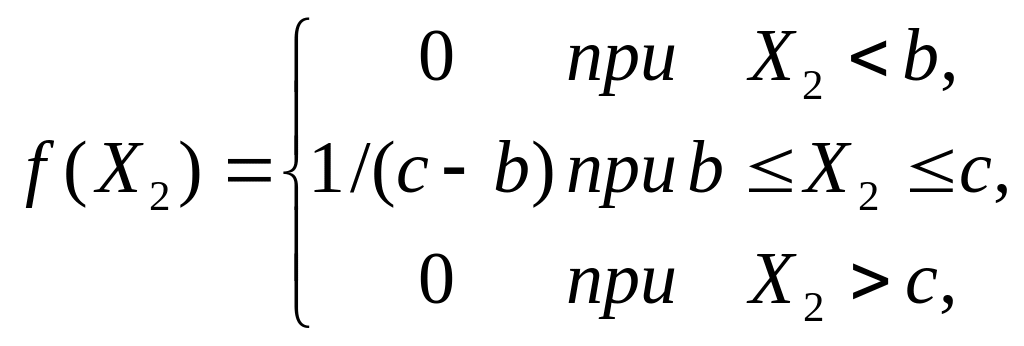
то плотность вероятности для случайной величины Y=X₁ +X₂

где Ф(α) вычисляется по формуле (2.36) с помощью таблицы для интеграла вероят­ности (см. табл. 1 Приложения).

Композиция равновероятного и гауссовского распределений может оказаться полезной для описания экспериментальных распределений производственных погре­шностей технологического процесса в тех случаях, когда наряду с действием многих случайных технологических факторов проявляется действие равномерно возраста­ющего или равномерно убывающего доминирующего фактора (старения формиру­ющего раствора при гальванической операции, старения фоторезистора и т. д.).