2.4. Основные понятия теории вероятностей и характеристики генеральной совокупности

Мы имеем дело с количественными признаками продукции, если результат каждого отдельного наблюдения выражается в числовом виде. В то же время на практике приходится иметь дело с такими показателями качества, когда результат каждого наблюдения основан на констатации, про­изошло или нет определенное событие. В отличие от количествен­ного признака показателя качества такой признак называют качест­венным. Примером качественного признака показателя качества может служить годное или бракованное изделие. В альтернативу «годное — бракованное» можно превратить и распреде­ление количественного признака продукции, используя заранее уста­новленные пределы изменения значения параметра качества (ε). Если значение параметра лежит внутри этого предела, то изделие является годным (хорошим), если вне их, то бракованным (плохим). Вполне очевидно, что попадание параметра очередного изделия в эти установленные пределы или за них является случайным собы­тием. Поэтому появление бракованного или годного изделия также случайное событие. Однако вероятность появления этого события можно предсказать заранее с помощью теории вероятности.

Предположим, что сдается готовая партия интегральных микро­схем. Известно, что в этой партии, состоящей из N интегральных микросхем, D бракованных. Тогда вероятность извлечь из этой партии именно бракованную будет

Q = D/N. (2.13)

Теперь предположим, что методом случайного отбора мы состави­ли из этой партии выборку объемом п. После проверки микросхем выборки выяснилось, что из п схем d микросхем оказались брако­ванными. Долю бракованных микросхем, полученных в результате опыта, обозначим через Q_oц. Эта доля называется частостью бракованных изделий или статистической вероятностью:

Q_ОП = d/n. (2.14)

Вполне очевидно, что Q — величина постоянная, определяемая количеством бракованных изделий D в партии. Величина же q_пa случайная.

Действительно, допустим, мы взяли выборку микросхем, напри­мер n=10, и среди них оказались три бракованные микросхемы. Согласно (2.14), имеем q_пa = 0,3. Вернув в генеральную совокупность первую выборку, опять методом случайного отбора составим выборку n = 10.

Пусть в ней теперь оказалась одна бракованная микросхема. Тогда q_оп =0,1. Аналогично можно составить третью выборку, чет­вертую и т. д. Как мы видим, величина q_aп может меняться, в то время как Q остается все время одинаковой для данной генеральной совокупности. Правда, при этом необходимо каждый раз возвра­щать выборку в генеральную совокупность. Величину Q называют генеральной характеристикой, q_оп — выборочной характеристикой.

Однако следует отметить, что статистическая вероятность при уве­личении числа опытов все более теряет свой случайный характер. Случайные обстоятельства, свойственные каждой отдельной выбор­ке, в массе взаимно погашаются, и средняя величина статистической вероятности с увеличением числа опытов приближается к генераль­ной характеристике Q. Это свойство, многократно проверенное экспериментально и подтверждающееся всем опытом практической деятельности, есть одна из наиболее характерных закономерностей, наблюдаемых в случайных явлениях.

Приведем некоторые теоремы, используемые при вычислении вероятности события.

Теорема сложения вероятностей. Вероятность появления хотя бы одного из нескольких попарно несовместимых событий равна сумме вероятностей этих событий. Для примера приведем контроль операции шлифовки полупроводниковой пластины при изготовлении микросхемы

Рассмотрим, например, событие, заключающееся в том, что контролируемая толщина пластины после операции шлифовки окажется меньше нижнего предела заданного допуска, и событие, заключающееся в том, что этот размер окажется больше верхнего предела допуска. Оба события несовместимы, так как исключают друг друга. Пусть на основе длительного наблюдения установлено, что вероятность первого события равна 0,03 (3%), а второго — 0,05 (5%). Тогда вероятность того, что рассматриваемая полупроводниковая пластина будет не соответствовать нор­мам стандарта (будет либо слишком тонкой, либо слишком толстой), равна сумме отдельных вероятностей, т. е. 0,03+0,05=0,08 (8%). А так как сумма вероятностей двух противоположных событий равна единице, то вероятность того, что пластина будет соответствовать требованиям стандарта, равна 1,00-0,08=0,92 (92%).

Теорема умножения вероятностей. Если событие состоит из двух или нескольких независимых событий и для появления такого сложного события необходимо появ­ление каждого события, то вероятность его равна произведению вероятностей от­дельных событий.

Предположим, что появление брака среди гибридных интегральных микросхем (ГИС) при монтаже активных элементов 0,02 (2%), а вероятность появления брако­ванных ГИС при создании на этих же схемах пассивных элементов равна 0,05 (5%). Оба события являются практически независимыми. Вероятность того, что при изготовлении ГИС появится бракованная микросхема за счет брака при монтаже навесных активных элементов и брака при создании пассивных элементов, равна произведению отдельных вероятностей: 0,02x0,05=0,001. Итак, среди 1000 схем в среднем окажется одна ГИС, которая будет иметь оба дефекта.

Теорема умножена вероятностей для зависимых событий. Вероятность совмест­ного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.

В качестве примера рассмотрим опять партию микросхем, состоящую из 100 шт., из которых три бракованные. Возьмем из этой партии одно за другим два изделия. Спрашивается: какова вероятность того, что оба изделия окажутся брако­ванными? Эти события зависимые, а именно* если первое изделие оказалось брако­ванным, то в партии осталось еще 99 шт., из которых 97 годных и 2 бракованные. Вероятность снова вытащить бракованное изделие составляет уже не 3/100, а 2/99. Вели бы первое извлеченное нами изделие оказалось годным, то среди оставшихся 99 шт. теперь находились бы три бракованные и вероятность того, что второй раз будет извлечено бракованное изделие, была бы равна 3/99. Итак, вероятность второго события зависит от результата первого

Вероятность того, что оба извлеченных изделия окажутся бракованными, равна 3/100 и 2/99. Вероятность же того, что извлеченные из этой партии последовательно друг за другом три изделия окажутся бракованными, равна (3/100)·(2/99)·(1/98)=1/16/700. Итак, можно утверждать, что из 161 700 опытов только в одном случае три последовательно извлеченные микросхемы окажутся бракованными.

Рассмотрим еще одно понятие в теории вероятностей, с которым нам в дальнейшем придется встречаться,— математическое ожи­дание. Математическое ожидание играет роль характеристики поло­жения случайной величины в генеральной совокупности, и поэтому его иногда называют генеральным средним арифметическим значе­нием случайной величины или центром группирования значений случайной величины в генеральной совокупности.

Рассмотрим случайную величину X, которая может принимать дискретные положения x₁ ,х₂ ,х₃ ,.., х_i ,.... х_n с соответствующими вероятностями p₁ ,р₂ ,р₃ ,…p_i ,…,p_n . Нам требуется охарактеризо­вать каким-то числом положение значения случайной величины на оси абсцисс с учетом того, что эти значения имеют различные вероятности. Для этой цели воспользуемся формулой для средней взвешенной, где каждое значение х_i при усреднении должно учиты­ваться с «весом», пропорциональным вероятности этого значения. Тогда генеральное среднее арифметическое значение случайной вели­чины X, которое обозначим М(х), может быть подсчитано по формуле

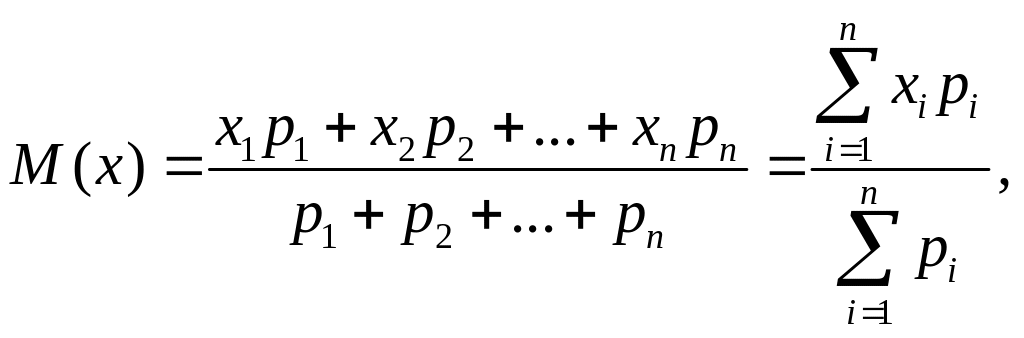(2.15)

или, учитывая, что (2.16)

(2.17)

Вычисленная на основании формул (2.3) и (2.4) выборочная средняя всегда будет содержать элемент случайности, в то время как математическое ожидание, представляющее среднее значение случайной величины в генеральной совокупности, является вели­чиной постоянной для данной генеральной совокупности. При боль­шом количестве наблюдаемых значений выборочная средняя при­ближается к математическому ожиданию.

Дисперсию случайной величины X в генеральной совокупности, которую будем обозначать через σ², подсчитывают по следующим формулам:

для случая, когда значения х_i в генеральной совокупности не повторяются,

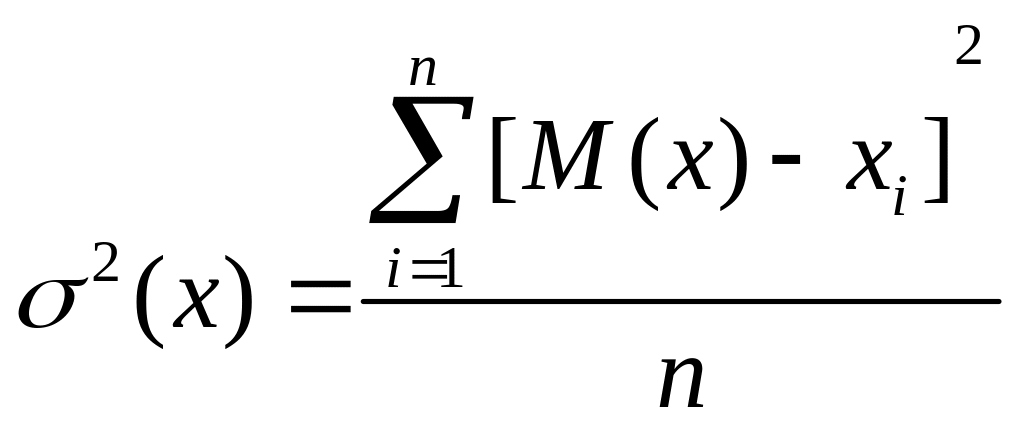(2.18)

для случая, когда значения х_i повторяются,

(2.19)

где

Кроме характеристик положения и рассеивания нам в дальнейшем придется столкнуться с рядом характеристик, каждая из которых описывает то или иное свойство распределения. В качестве этих характеристик чаще всего применяются так называемые центральные моменты.

Практический интерес представляют второй, третий и четвертый центральные моменты. Второй центральный момент представляет собой не что иное, как дисперсию.

Третий центральный момент служит для характеристики асимметрии распределения:

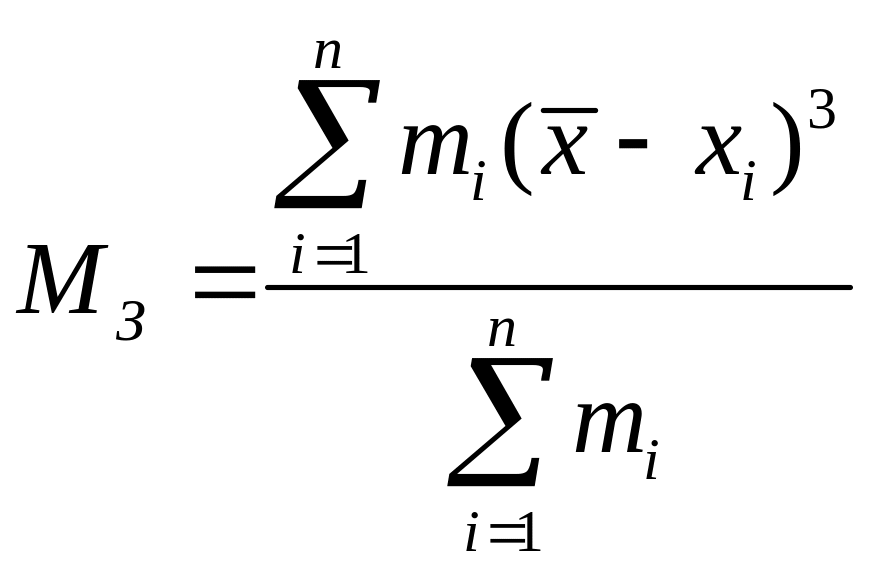(2.20)

Если распределение симметрично относительно его среднего значения, то взве­шенные по соответствующим частотам кубические отклонения значений случайной величины, равноотстоящие от средней арифметической, отличаются только знаками и их сумма равна нулю. Если же распределение асимметрично, то значения парамет­ра, лежащие по одну сторону от средней арифметической, дадут большие кубические отклонения, чем значения, лежащие по другую сторону. Знаки этих отклонений различны. Разность между суммами положительных и отрицательных слагаемых будет отличаться от нуля, являясь положительной или отрицательной. Соответственно этому знак М₃ указывает на отрицательную или положительную асимметрию.

Чтобы получить меру асимметрии в виде отвлеченного числа, позвозляющего сравнивать разнородные распределения, третий момент М₃ делят на куб стандарт­ного отклонения σ³. Полученная величина, обозначаемая А, носит название асим­метрии или косости распределения:

А = М₃ / σ³ (2.21)

Величина асимметрии дает нам представление о большей или меньшей асимметрии, а знак указывает на ее направление: если А>0, то средняя лежит справа от моды (правосторонняя асимметрия); если А<0, то средняя лежит слева от моды (левосто­ронняя асимметрия).

Кроме значения А за меру асимметрии иногда принимают число

а=( -Мо)/ σ, (2.22)

которое часто называют коэффициентом асимметрии

Особенностью симметричных рядов является равенство трех характеристик — средней арифметической, моды и медианы: = Мо = Ме. Поэтому а для симметрич­ных распределений равно нулю.

Четвертый центральный момент М₄ служит для характеристики так называемой крутости, т. е. островершинности или плосковершинности распределения. Это свой­ство распределения описывается с помощью так называемого эксцесса.

Эксцесс случайной величины X вычисляется по формуле

Эк=М₄ / σ⁴ -3. (2.23)

Число 3 вычитается из отношения М₄ / σ⁴ потому, что для весьма важного и широко распространенного в природе гауссовского закона распределения, с которым мы подробно познакомимся в дальнейшем, М₄ / σ⁴ = 3. Поэтому для гауссовского рас­пределения эксцесс равен нулю. Кривые, более островершинные по сравнению с ним, обладают положительным эксцессом; кривые более плосковершинные — отрица­тельным эксцессом.