4.4. Оценка генеральной характеристики рассеивания σ с помощью выборочных характеристик рассеивания

Если среднее значение характеризует настроенность технологи­ческого процесса, то величина стандартного отклонения характери­зует его качество и поэтому является одной из важнейших харак­теристик при анализе и контроле качества изделий.

Оценка σ по . На практике распространенной ошибкой является необоснованная замена неизвестного стандартного от­клонения генеральной совокупности σ выборочным стандартным отклонением s.

Стандартное (среднее квадратическое) отклонение s одной вы­борки, особенно при малом ее объеме, не может считаться пригод­ным значением оценки стандартного отклонения генеральной сово­купности, так как, кроме всего прочего, средняя арифметическая , которая используется при вычислении стандартного отклонения выборки, является выборочной средней, а не математическим ожи­данием генеральной совокупности. Поэтому и средняя арифмети­ческая значений s из k выборок также не идентична σ.

Поскольку теоретически можно получить распределение стан­дартных отклонений выборок одинакового объема n, взятых из совокупности с гауссовским распределением, можно говорить о свя­зи между и σ. Отношение к σ обозначим через С₂. Оно меньше единицы и приближается к единице по мере увеличения п. Коэф­фициент С₂ можно использовать для оценки неизвестного стандарт­ного отклонения генеральной совокупности σ по , т. е. по средней арифметической значений стандартного отклонения ряда выборок одинакового объема п. Можно считать, что с достаточной точ­ностью выполняется равенство [8]

(4.14)

Значения С₂ зависят от объема выборок и приведены в табл. 7 Приложения.

Учитывая, что при вычислении выборочной дисперсии измен­чивость делят не на число наблюдаемых значений п случайной величины х, а на число степеней свободы v = n — 1, для вычисления оценки стандартного отклонения генеральной совокупности исполь­зуют коэффициент С₂, умноженный на , т. е.

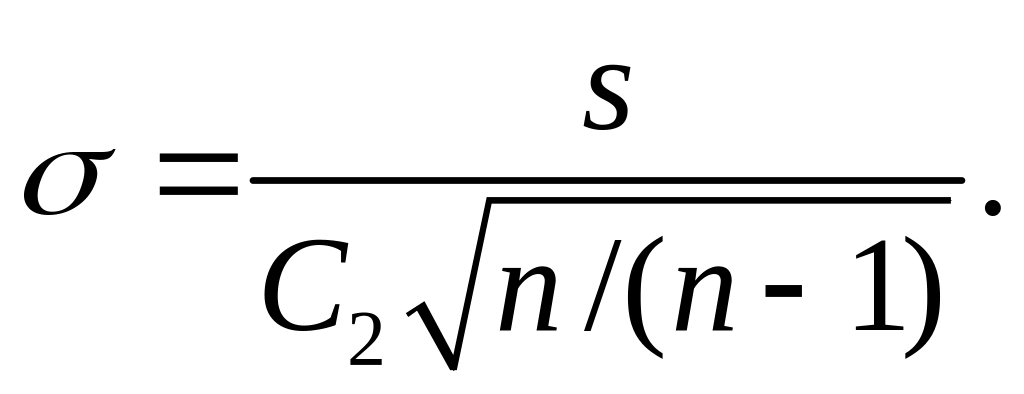(4.15)

При объеме выборки п> 10 для оценки σ можно с малой погреш­ностью пользоваться формулой (14).

При анализе и контроле технологических процессов часто встает задача не просто оценить значение σ по , а определить величину вероятности равенства неизвестной генеральной дисперсии (или ста­ндартного отклонения) и среднего значения выборочной дисперсии (или среднего значения стандартного отклонения выборки). При этом иногда приравнивают неизвестное генеральное стандартное отклонение σ выборочному стандартному отклонению s, допуская большую погрешность, чем при замене σ на . Когда задача о заме­не решена, то говорят, что, полагая σ ≈ (или s), σ находим с точ­ностью ε и вероятностью Р=Р₁ —Р₂.

Решение этой задачи записывается обычно (как указывалось в § 2) так: вероятность того, что σ будет находиться в пределах - ε ≤ σ ≤ + ε, равна разности вероятностей двух событий; + ε≥ σ и - ε ≤ σ, т. е.

P{ - ε ≤ σ ≤ + ε }=P₁-P₂, (4.16)

где Р₁ и Р₂ — вероятности, определяемые по таблице значений вероятностей Р для критерия χ² (см. табл. 2 Приложения) соответ­ственно для значений

и (4.17)

и для v = N - k, где N=nk.

В случае замены σ на s в числителе выражения (4.17) вместо N— k будет п— 1, а число степеней свободы v = n—1.

Разделив неравенство, стоящее в фигурных скобках выражения (4.16), на , получим

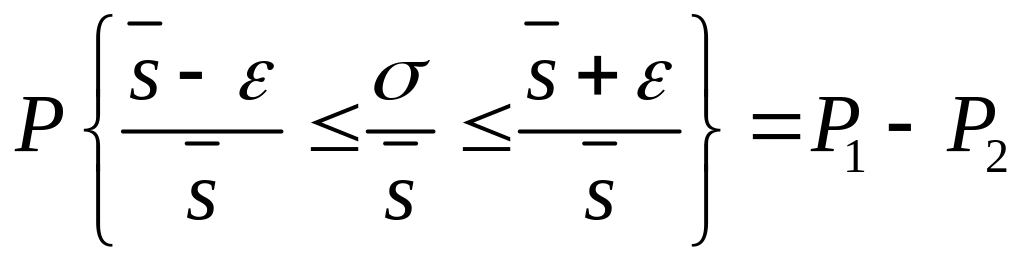
или с учетом (4.17)

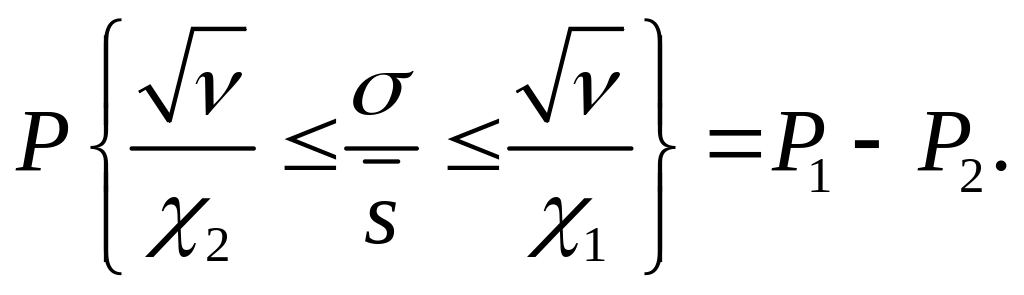(4.18)

Для случая дисперсий выражение (18) примет следующий вид:

Переписав это выражение в удобном виде, будем иметь

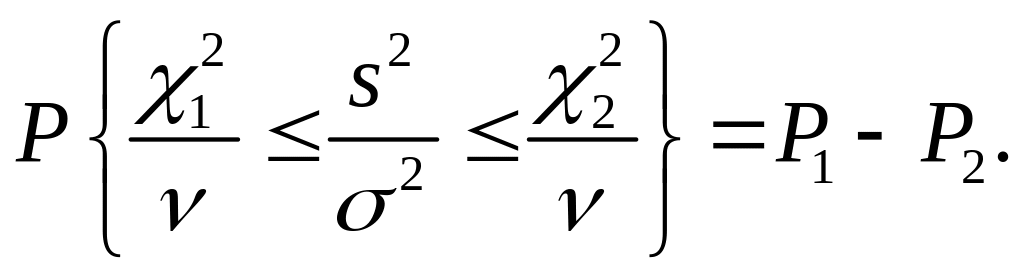(4.19)

Оценка замены неизвестного стандартного отклонения генеральной совокупности σ выборочным стандартным отклонением s рассмот­рена в примере 6 § 2.7.

Оценка σ по R. В связи с тем, что вычисление стандартного отклонения s связано с трудностями, в качестве меры отклонения отдельных значений внутри выборки используют размах R, кото­рый легко определяется для выборок небольшого объема. Теорией и практикой доказано, что стандартное отклонение s и размах R выборки находятся в прямой пропорциональной зависимости; между ними существует положительная корреляционная связь, т. е. чем меньше s, тем меньше R , и наоборот.

Поэтому можно доказать, что если выборки производятся из генеральной совокупности с гауссовским законом распределения или законом, близким к нему, то при достаточно большом числе выборок k математическое ожидание величины R/d₂ (где d₂ — неко­торый коэффициент, зависящий от объема п выборок) равно σ , т. е.

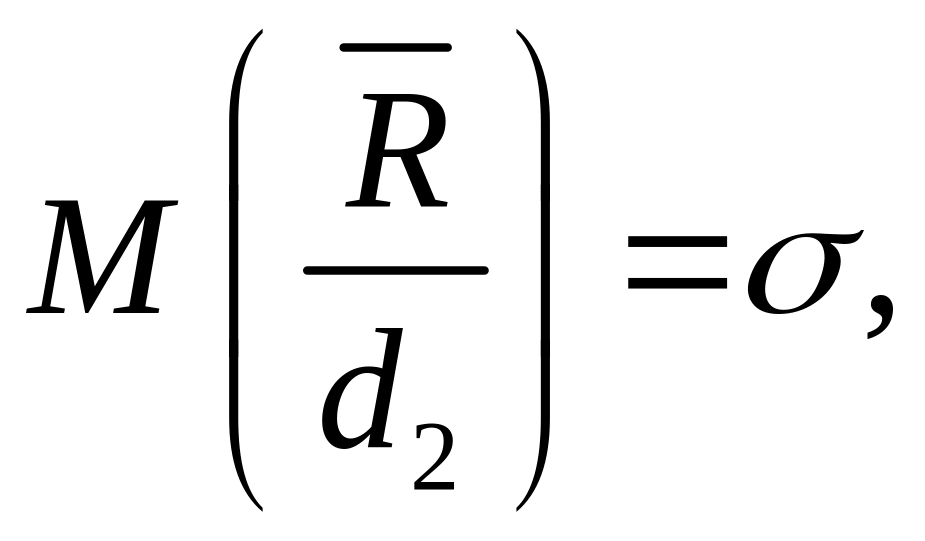
Это дает нам право использовать среднее значение размахов вариации R_i из k выборок в качестве оценки стандартного отклоне­ния генеральной совокупности, так же как и . Стандартное отклоне­ние генеральной совокупности σ связано с при помощи следу­ющей зависимости:

σ = /d₂. (4.20)

Значение d₂ в (4.18) определяется в зависимости от п по табл. 7 Приложения.