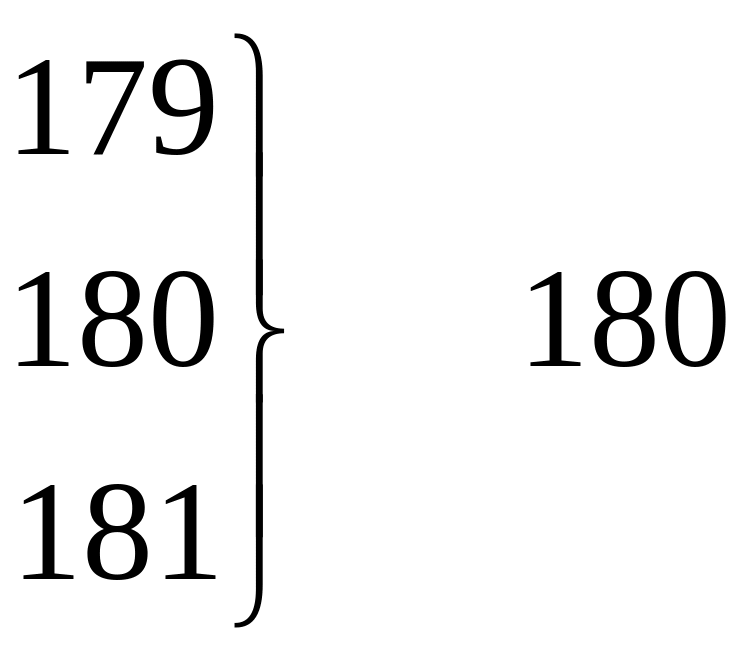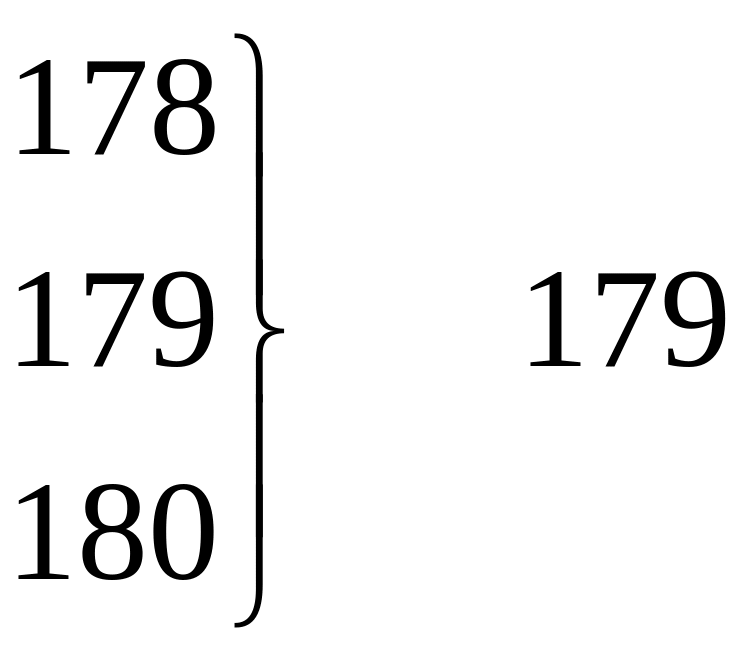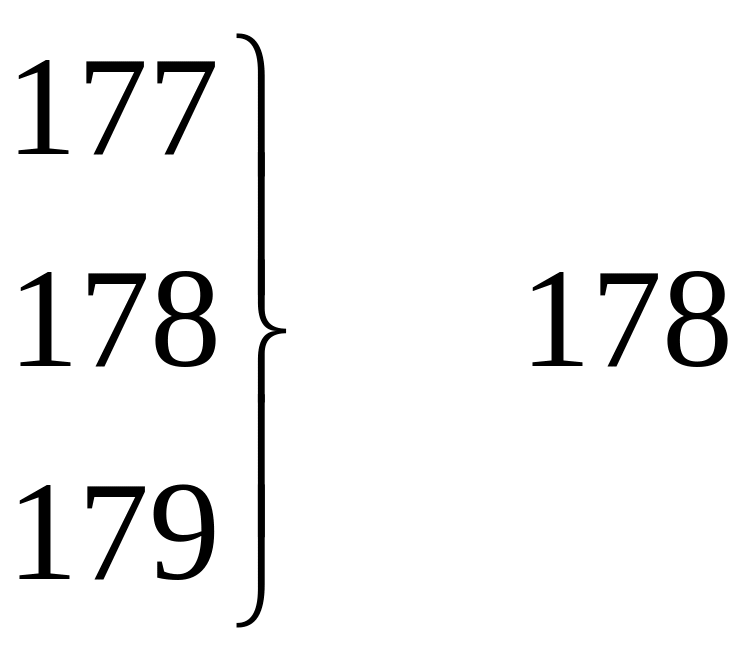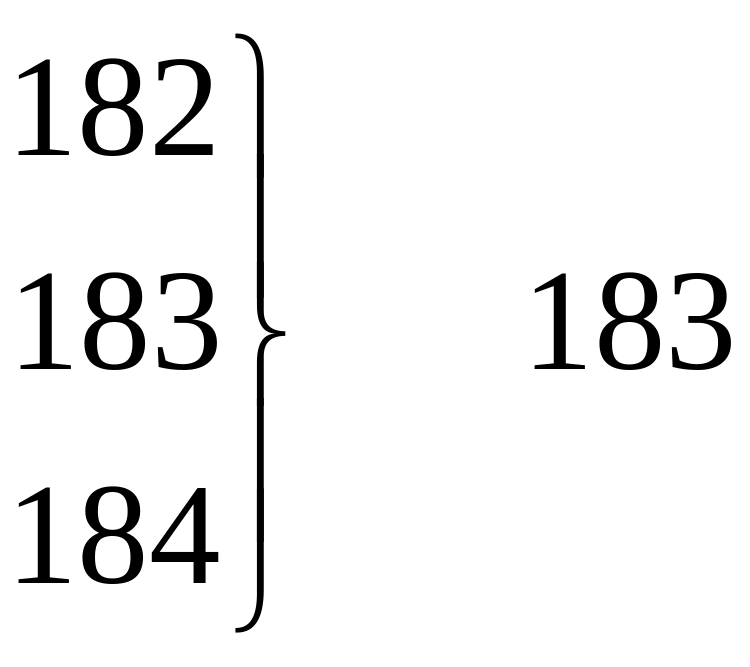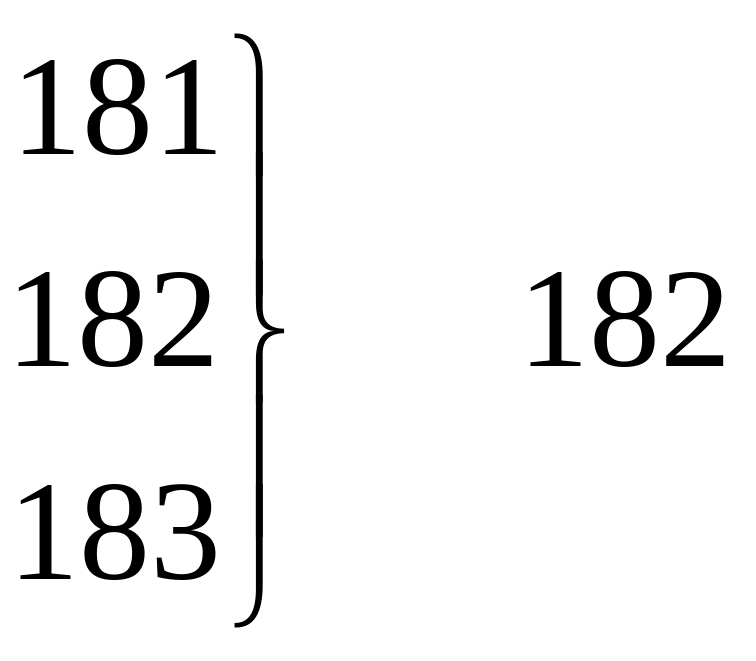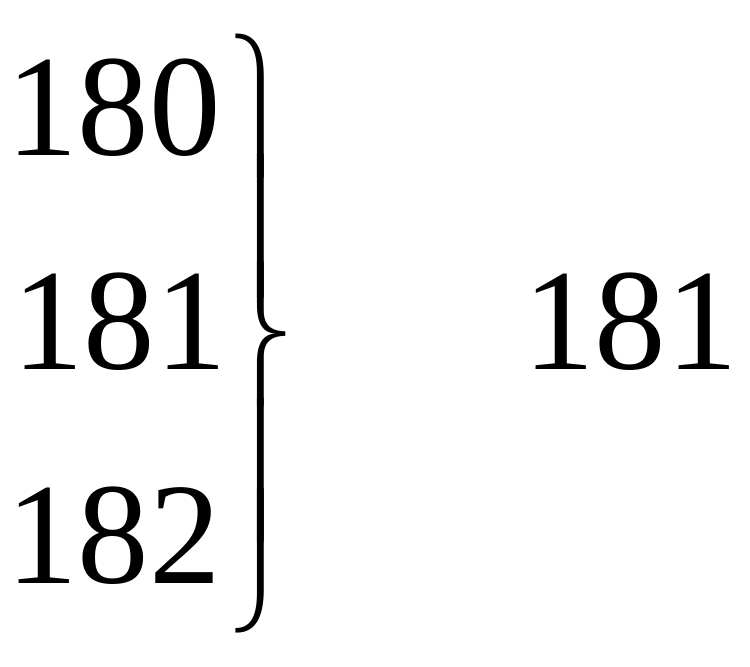В.С. Скоробогатов

Математико-статистические методы обработки данных при управлении качеством электронных средств

Воронеж 2003

МИНИСТЕРСТВО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Воронежский государственный технический

университет

В.С. Скоробогатов

Математико-статистические методы обработки данных при управлении качеством электронных средств Утверждено редакционно-издательским советом

университета в качестве учебного пособия

В оронеж 2003

УДК 678.029.983

Математико-статистические методы обработки данных при управлении качеством электронных средств: Учеб. пособие. / В.С. Скоробогатов. Воронеж: Воронеж. гос. тех. ун-т, 2003. 152 с.

В учебном пособии рассматриваются математико-статистические основы обработки данных при управлении качеством электронных средств: статистический ряд, методы его представления и обработки, расслоение статистических данных и статистические методы оценки качества электронных средств.

Пособие предназначено для студентов вузов специальности 200800 "Проектирование и технология производства РЭС" и является дополнительным материалом при изучении дисциплины "Управление качеством электронных средств".

Учебное пособие подготовлено в электронном виде в текстовом редакторе MS Word XP и содержится в файле МАТ-СТАТ МЕТОДЫ12.doc.

Табл. 31. Ил. 31. Библиогр.: 8 назв.

Научный редактор д-р техн. наук, проф. А.В. Муратов.

Рецензенты: НТС ОАО "Электросигнал", г. Воронеж;

д-р техн. наук, проф. Ю.А. Цеханов

 Скоробогатов В.С., 2003

 Оформление. Воронежский государственный технический университет, 2003

Введение

В настоящее время уже очевидно, что конкурентоспособность любого предприятия, независимо от формы его собственности и его размеров зависит в первую очередь от качества его продукции и соизмеримости ее цены с предлагаемым качеством, т.е. от того, в какой степени продукция предприятия удовлетворяет запросы потребителя.

Качество любого изделия - это совокупность свойств этого изделия, обусловливающая возможность его применения, удовлетворяющую определенным требованиям потребителя.

Параметры объекта, характеризующие его качество, называют параметрами качества.

Совокупность этапов проектирования изделия, его изготовления и эксплуатации составляет жизненный цикл изделия, который все время повторяется.

Качество изделия, являясь его свойством, закладывается в изделие в процессе его проектирования и изготовления, а оценивается в процессе его эксплуатации. Однако обеспечение планируемого качества и соответствующая ему корректировка параметров качества на этапах проектирования и изготовления изделия требуют решения вопроса как обеспечения, так и контроля качества на всех трех этапах жизненного цикла изделия.

1. Общие сведения о контроле качества электронных средств

Контроль качества осуществляется путем сравнения запланированного показателя качества с действительным его значением, а если качество можно контролировать, то, следовательно, им можно и управлять. Собственно конт­роль качества, например процесса производства, и состоит в том, чтобы, про­веряя нужным образом подобранные выборочные данные (показатели каче­ства), обнаружить отклонение показателей качества от запланированных их значений. В случае обнаружения такого отклонения производитель ищет при­чину его появления и после корректировки процесса вновь проверяет соответ­ствие скорректированных показателей качества запланированным их значени­ям (стандарту или норме). Именно по такому непрерывному циклу осуществ­ляются управление и обеспечение требуемого качества и дальнейшее его улуч­шение. Учитывая последовательность прохождения в этом цикле таких важней­ших этапов, как план (PLAN), реализация (DO), проверка (CHECK) и ис­правление (ACTION), его называют PDCA-циклом или циклом Деминга, который использовал эти понятия в своих семинарах в Японии [1,2].

Если все показатели качества контролируемого изделия система­тизированы и осуществляется системный подход к обеспечению и контролю качества с целью анализа и управления составляющих качества на каждом этапе жизненного цикла изделия, то можно говорить о наличии системы управления качеством. Таким обра­зом, система управления качеством рассматривает вопросы как обеспечения, так и контроля качества изделий в течение всего их жизненного цикла, начиная с момента составления технического задания и заканчивая рассмотрением претензий заказчика на гото­вую продукцию. Если в системе управления качеством для обеспече­ния контроля качества изделий на всех этапах его жизненного цикла применяется вычислительная техника (ЭВМ, микропроцессоры, вы­числительные устройства), то говорят о наличии автоматизирован­ной системы управления качеством [3].

В то же время трудности создания системы управления каче­ством заключаются в том, что целый ряд изделий, к которым в первую очередь относятся электронные средства, характеризуются большим количеством и многообразием показателей качества, ко­торые, в свою очередь, делятся на два основных класса: количест­венные показатели (физические, электрические, механические, хи­мические величины); качественные показатели, оцениваемые не кон­кретными значениями величины, а с помощью чувственных органов человека (зрительными органами, например восприятие цвета; обо­нянием — восприятие запахов, и т. п.).

Следует отметить, что управление качеством возможно только в том случае, если возможно управле­ние факторами, воздействующими на рассматриваемый параметр качества. В то же время если исследуемый объект рассматривать в виде «черного ящика» (рис. 1.1), то все разнообразие факторов, воздействующих на параметр качества (Y) объекта, можно условно разбить на три самостоятельные группы [3].

Первая группа факторов составляет k-мерный вектор X входных управляемых параметров, т. е. таких, которые можно измерять и целенаправленно изменять, поддерживая при этом заданные зна­чения показателя качества Y. Вектор X называют вектором фак­торов; область его возможных значений (х₁, x₂, х₃,.... x_k) — фа­кторным пространством, а его составляющие — факто­рами.

Вторая группа образует р-мерный вектор W контролируе­мых, но в рассматриваемой тех­нологической операции не упра­вляемых параметров , ха­рактеризующих состояние ис­ходных факторов и качество объекта в целом (например, чи­стота исходного кремния при из­готовлении микросхем).

Третья группа составляет т-мерный вектор Z неконтролируемых, а следовательно, и неуправля­емых параметров Сюда относятся параметры, оказыва­ющие случайные возмущающие воздействия на качество объекта.

Очевидно, что выход системы Y может состоять из любого числа параметров качества , интересующих нас обычно не в одинаковой степени. Система управления качеством рассматрива­ет на каждом этапе жизненного цикла изделия (или отдельного периода цикла) только контролируемые и управляемые факторы, оказывающие влияние на параметры качества объекта управления.

Рис. 1.1. Схема процесса в виде «черного ящика»

Еще в 20-х годах прошлого века специалисты поняли, что различные изменения параметров качества в производственном процессе могут быть описаны с помощью статистических методов. В 40-50-х годах методы статистической обработки и анализа экспериментальных данных были развиты и усовершенствованы.

Применение статистических методов - весьма дейст­венный путь разработки новой технологии и контроля качества производственных процессов. Многие ведущие фирмы стремятся к их активному использованию, и не­которые из них тратят более ста часов ежегодно на обуче­ние этим методам, осуществляемое в рамках самой фир­мы. Хотя знание статистических методов - часть нор­мального образования инженера, само знание еще не оз­начает умения применить его. Способность рассматри­вать события с точки зрения статистики важнее, чем зна­ние самих методов. Кроме того, надо уметь честно при­знавать недостатки и возникшие изменения и собирать соответствующую информацию. Следует подчеркнуть, что важно не столько знание самих статисти­ческих методов, сколько сознательное желание использо­вать их [1].

Контролем охватываются все этапы производства ЭС. В зависи­мости от стадии «жизни» изделия (производство, хранение, эксплуатация) различают производственный контроль и эксплуатацион­ный.

Производственный контроль, т. е. статистический контроль, осу­ществляемый на стадии производства, охватывает, как правило, все вспомогательные, подготовительные и технологические операции. В зависимости от места в цепи технологического процесса производственный контроль подразделяют на входной, операционный и приемочный.

Входной контроль — это контроль продукции поставщика, по­ступившей к потребителю или заказчику и предназначенной для использования при изготовлении, ремонте или эксплуатации ЭС. Поступающие в производство материалы, полуфабрикаты, комп­лектующие изделия подвергаются входному контролю на их соот­ветствие требованиям технической документации (ТУ, чертеж на изделие).

Операционный контроль включает в себя контроль продукции после завершения какой-либо операции.

Приемочный контроль предусматривает контроль готовой про­дукции по окончании всех технологических операций.

Эксплуатационный контроль, т. е. статистический контроль, осу­ществляемый на стадии эксплуатации продукции, охватывает эксп­луатируемые ЭС.

Статистический контроль в основном базируется на контроле фактических значений параметров качества и сравнении их значений с запланированными в соответствии с разработанной нормативно-технической документацией (НТД). Поэтому такой контроль каче­ства часто называют параметрическим контролем.

Кроме того, при приемочном и операционном контроле качества ЭС на конечных операциях их изготовления, а также при эксплу­атационном контроле ЭС, как правило, производится их контроль на качество функционирования в соответствии с их дальнейшим назначением. Этот вид контроля ЭС называют функциональным контролем.

Перечисленные виды контроля могут быть сплошными (100 %) или выборочными.

Сплошной контроль предусматривает проверку каждой единицы продукции.

При выборочном контроле подвергаются проверке выборки, про­изводимые из больших партий изделий.

При любом виде контроля проводятся измерения какого-либо параметра, набирается статистический материал, который затем обрабатывается статистическими методами, анализируется и используется при управлении качеством электронных средств.

2. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ОСНОВЫ

УПРАВЛЕНИЯ КАЧЕСТВОМ

2.1. Статистический ряд и его обработка

при управлении качеством

В основе управления качеством лежат различные статистические методы. Для их применения необходимо набрать достаточное количество статистических данных по параметрам качества изделий. Как правило, эти данные являются случай­ными величинами, т. е. могут принимать то или иное значение, причём заранее не известно, какое именно. Сбор и обработка статистических данных основаны на применении так называемого выборочного метода.

Выборкой называют часть изделий, отобранных из общей их совокупности для получения информации о всем количестве изделий, называемом общей или генеральной совокупностью. При этом последняя подразумевает однородную совокупность параметров качества контролируемых изделий. Если выборка достаточно хорошо представляет соответствующие характеристики генеральной совокупности, то такую выборку называют представительной или репрезентативной.

При анализе и контроле технологических процессов выборку классифицируют по ряду признаков, например по способу отбора (повторные и бесповторные), преднамеренности отбора (пристраст­ные и случайные), по отношению ко времени отбора (единовремен­ные и текущие), целевому назначению (общепроизводственные, одноагрегатные) и т. д.

Повторная выборка образуется отбором изделий из генеральной совокупности для измерения параметров качества, после чего они возвращаются в совокупность. Такая операция может быть прове­яна многократно. При бесповторной выборке отобранные изделия не возвращаются в генеральную совокупность. При этом гарантируется, что ни одно изделие не попадает дважды в выборку.

Если при отборе изделий из генеральной совокупности отдается предпочтение изделиям с заранее оговоренным признаком, то такую выборку называют пристрастной или расслоенной. Если же возможность попадания в выборку каждого из изделий равновероятна, то такую выборку называют случайной, например, изделия отбираются наугад из разных источников (разные поточные линии» разные единицы оборудования и т. д.).

Единовременная выборка образуется из партии изделий после их изготовления независимо от того, в какой момент времени изготов­лено каждое из них. Текущая выборка в отличие от единовременной состоит из изделий, последовательно изготовленных за определен­ный промежуток времени. Общепроизводственная выборка служит для получения общей оценки технологического процесса независимо от того, сколько поточных линий, единиц оборудования и т. д. занято в производственном процессе. Одноагрегатная выборка со­ставляется из изделий, изготовленных на определенном оборудовании(агрегате).

Помимо названных выше применяют и другие, так называемые экспериментальные, выборки, предназначенные для анализа точно­сти и стабильности отдельных технологических операций, изучения влияния технологических режимов отдельного оборудования, осна­стки на точность и стабильность качества продукции и других целей. Значение параметра качества отдельного изделия (например, глубина диффузии примеси при изготовлении интегральной микро­схемы), взятого из текущего процесса, изменяется от изделия к из­делию. Если при изготовлении изделий отбирать выборки, то ста­тистические характеристики этих выборок тоже будут колебаться. Если же по статистическим характеристикам выборок нужно сде­лать вывод о числовых характеристиках (параметрах) генеральной совокупности, то для этого менее благоприятна выборка малого объема, чем большого. Но все-таки выгоднее вместо одной исполь­зовать несколько выборок малого объема, охватывающих большой промежуток времени. При этом представление о системе случайных причин, воздействующих на процесс изготовления, т. е. о всей генеральной совокупности, будет более полным.

Значение параметров качества изделий выборки представляет собой первичный статистический материал, подлежащий обработке, осмыслению и научному анализу.

Предположим, что имеются результаты наблюдений над случай­ной величиной х. Для представления полученной информации о ка­честве изделия в управляющую подсистему статистический матери­ал подвергается специальной обработке в измерительной подсисте­ме. Сначала измеренные значения параметра располагаются в воз­растающем или убывающем порядке с тем, чтобы получить так называемый упорядоченный (ранжированный) ряд или упорядочен­ное распределение различных значений одного и того же параметра качества.

В табл. 2.1 приведены результаты измерений пробивного напря­жения диэлектрических слоев 160 однотипных МОП-структур.

Статистический материал такого вида подвергают дополнитель­ной обработке — строится так называемый статистический ряд, в котором одни и те же значения случайной величины объединяют. Число случаев для каждого из повторяющихся значений (m₁, m₂,m₃,.... т_n) называют абсолютной частотой или статистическим весом. Найдя в табл. 2.1 наибольшее и наименьшее значения (210 и 179), составим таблицу, в которой расположим результаты измерений от 179 до 210 В в порядке возрастания.

Для подсчета частоты можно отмечать штрихами одинаковые значения по мере просмотра всех данных. В результате получаем упорядоченный ряд из 160 наблюдений (табл. 2.2а).

Таблица 2.1

Пробивные напряжения диэлектрических слоёв 160 однотипных МОП-структур, В
191 199 189 188 188 195 187 201 188 199 185 193 193 193 187 202	197 198 196 193 196 179 187 201 197 207 201 206 196 190 188 205	195 196 198 187 197 182 191 192 190 188 199 192 201 197 191 196	197 187 202 198 196 193 204 193 185 191 205 197 205 198 209 198	194 191 195 195 188 201 193 198 184 193 190 192 193 204 198 199	194 194 192 187 188 199 196 202 196 183 198 184 193 205 199 202	193 195 197 180 191 186 195 193 201 189 198 188 193 194 192 193	203 197 197 197 203 190 187 186 209 198 203 202 207 197 190 190	203 193 199 202 188 198 187 194 188 190 189 204 199 200 196 193	198 210 192 187 198 195 201 197 194 208 195 181 193 205 203 195

Числа, стоящие в столбце х, называют упорядоченным рядом параметра качества, а числа, стоящие в столбце m— рядом частот. Табл. 2.2а дает более наглядную картину изменения значений пара­метра качества, чем табл. 2.1. Структуры с пробивным напряжени­ем от 190 до 199 В встречаются чаще других, а структуры с пробив­ным напряжением меньше 179 и больше 210 В вообще не встречают­ся. Из табл. 2.2а видно, как распределяются значения пробивных напряжений 160 измеренных структур в пределах от 179 до 210 В.

В реальных условиях важно, чтобы данные регистрировались в простой и доступной для использования форме.

Таблица 2.2а

Упорядоченный статистический ряд наблюдения, составленный по результатам намерений пробивного напряжения диэлектрических слоев 160 однотипных

МОП-структур (контрольный лист)

X		т	X		m
179	/	1	195	/////////	9
180	/	1	196	////////	8
181	/	1	197	//////////////	14
182	/	1	198	//////////	10
183	/	1	199	//////////	10
184	//	2	200	/	1
185	//	2	201	///////	7
186	//	2	202	//////	6
187	/////////	9	203	/////	5
188	//////////	10	204	///	3
189	///	3	205	/////	5
190	///////	7	206	/	1
191	//////	6	207	//	2
192	//////	6	208	/	1
193	/////////////////	17	209	//	2
194	//////	6	210	/	1
				Сумма	160

Для этого широкое распространение получил контрольный листок - бумажный бланк, на котором заранее напечатаны контролируемые параметры, с тем, чтобы можно было легко и точно записать данные измерений (табл. 2.2б). Его главное назначение облегчить процесс сбора данных и автоматически упорядочить данные для облегчения их дальнейшего использования. Каждый раз, когда производится замер, в соответствующую клеточку ставится крест, так, что к концу измерений гистограмма готова.

Таблица 2.2б

Контрольный листок для регистрации распределения

измеряемого параметра качества в ходе производственного процесса (значение параметра на чертеже 8,3000,008)

	Отклонение	Замеры															Частота
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
	-10
	-9
*	-8
	-7
	-6
	-5																1
	-4																2
	-3																4
	-2																6
	-1																9
8,300	0																11
	1																8
	2																7
	3																3
	4																2
	5																1
	6																1
	7
*	8
	9
	10
* Граница поля допуска (по чертежу) Итого																	55

Изменение параметра качества может быть дискретным или непрерывным. Дискретным изменением параметра качества назы­вают такое, при котором рядом лежащие значения в ранжирован­ном ряду отличаются одно от другого на некоторую конечную величину (обычно целое число). Примером дискретного изменения случайной величины может быть число дефектных изделий в выборках, которые периодически берутся из текущего технологического процесса. Число дефектных изделий может быть только целым.

Непрерывным изменением параметра качества называют такое, при котором рядом лежащие его значения в ранжированном ряду отличаются одно от другого на сколь угодно малую величину. Примером непрерывного изменения случайной величины может служить изменение пробивного напряжения; хотя, например, за­фиксирован результат измерения — 197 В, пробивное напряжение на диэлектрике обследуемой структуры не обязательно точно равно этому числу. Если применять более точный измерительный прибор, то результат может оказаться равным, например, 196,86 или 197,32 В.

В любом из этих двух случаев измеренное значение находится ближе к 197, чем к 196 или 198 В. Итак, если у 14 структур, зафиксировано пробивное напряжение 197 В, то в действительности значение каждого из них колеблется в пределах, от 166,5 до 197,4 В. При непрерывном изменении параметра качества его распределение называют интервальным.

За величину интервала (его также называют классом), как прави­ло, принимают его середину, т. е. центральное значение.

Если значение случайной величины находится в точности на границе двух классов, то можно считать (чисто условно) данное значение принадлежащим в равной мере к обоим классам и прибав­лять одну его половину к верхнему, а другую половину — к нижне­му классу. Наряду с этим правилом можно рекомендовать придер­живаться следующего порядка:. в каждый класс включаются те наблюдения, числовые значения которых больше нижней границы класса и меньше или равны верхней.

Число классов, на которые следует группировать статистический материал, не должно быть слишком большим (тогда ряд распреде­ления становится невыразительным и частоты в нем обнаруживают незакономерные колебания), но не должно быть и слишком малым (тогда свойства распределения описываются статистическим радом слишком грубо). Практика показывает, что при достаточно боль­шом числе наблюдений рационально выбирать 10...20 классов. Ши­рина классов (длина интервалов) может быть как одинаковой, так и различной. Проще брать ее одинаковой. В этом случае ширина класса подсчитывается по формуле

, (2.1)

где x_i, x_i+1 — границы i-го класса; x_max, х_min — максимальное и ми­нимальное значения; k — число классов.

При формировании данных о случайных величинах, распреде­ленных крайне неравномерно, более удобно выбирать в области наибольшей плотности распределения ширину классов более узкую, чем в области малой плотности. В случае неодинаковой ширины классов удобнее пользоваться не абсолютной величиной m_i, а от­носительной, равной отношению частоты m_i приходящейся на i-й класс или i-е значение параметра, к общему числу наблюдений n:

w_i=m_i /n. (2.2)

Эту относительную величину называют относительной часто­той или частостью.

Нетрудно заметить, что сумма частостей всех интервалов равна единице, или 100%.

Если заранее подготовить бланки в виде табл. 2.2а и, производя измерения, вести ее заполнение, заранее выбрав классы (интервалы), то легко узнать состояние производства и качество произведенных за день изделий. Такие таблицы обычно называют контрольными листами. Анализ производства по контрольному листу, являюще­муся одним из семи инструментов качества,— основа аналитичес­кой работы; он несет большой объем информации.

Приведенное в табл. 2.2а распределение пробивного напряжения имеет 32 интервала, каждый из которых равен 1 В. Для представле­ния данных табл. 2.2а в виде интервального ряда распределения необходимо значительно уменьшить число интервалов. Для этого объединим по три значения показателя качества так, чтобы получи­лись классы шириной 3 В. Способы такого объединения показаны в табл. 2.3.

Таблица 2.3

Способы объединения наблюдаемых

значений показателей качества

Способ 1		Способ 2		Способ 3
середина интервала	mi	середина интервала	mi	середина интервала	mi
	3		2		1
	4		3		3
и т.д.		и т.д.		и т.д.

Как видно из таблицы, при втором и третьем способах к числу 179 подключаются соответственно еще одно или два значе­ния.

Так как эти значения при измерении пробивного напряжения 160 структур не наблюдались, то их частоты равны нулю. То же самое справедливо для числа 210, замыкающего упорядоченный ряд. Если воспользоваться третьим способом, то получим интервальный ряд распределения с числом классов k =12 и шириной класса, равной 2,9 В. Такой ряд приведен в табл. 2.4.

Таблица 2.4

Интервальный ряд распределения пробивных напряжений

диэлектрических слоев 160 однотипных МОП-структур

Интервал (класс)	Середина интервала (класса)	Частота mi	Относитель­ная частота wi%	Накоплен­ная частота	Относитель­ная накоплённая частота
176,5...179,4	178	1	0,6	1	0,6
179.5...182.4	181	3	1,9	4	2,5
182,5... 185,4	184	5	3,1	9	5,6
185,5...188,4	187	21	13,1	30	18,1
188,5...191,4	190	16	10,0	46	28,7
191,5...194,4	193	29	18,1	75	46,8
194,5...197,4	196	31	19,4	106	66,2
197,5..200.4	199	21	13,1	127	79,3
200,5...203,4	202	18	11,4	145	90,7
203,5...206,4	205	9	5,6	154	96,3
206,5...209,4	208	5	3,1	159	99,4
209,5...212,4	211	1	0,6	160	100,0