4. Приближенное решение систем линейных дифференциальных уравнений

Теоретические сведения

Рассмотрим систему двух дифференциальных уравнений

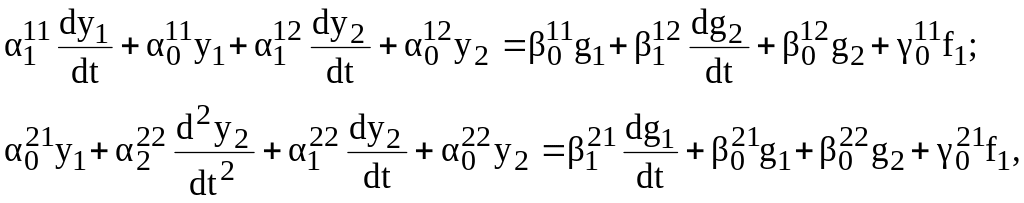
в которой t  независимая переменная;

g₁(t), g₂(t), f(t) известные функции переменной t;

y₁(t), y₂(t) искомые функции переменной t;

 постоянные коэффициенты, где i соответствует порядку производной функций g, f или y; j  номер дифференциального уравнения (номер строки); k  соответствует индексу (номеру) функции g_k, f_k, y_k.

Переходя к операторной форме записи эту систему можно представить в виде:

a₁₁(p)y₁ + a₁₂(p) y₂ = b₁₁(p) g₁ + b₁₂(p) g₂ + c₁₁(p) f₁;

a₂₁(p) y₁ + a₂₂(p) y₂ = b₂₁(p) g₁ + b₂₂(p) g₂ + c₂₁(p) f₁,

в котором коэффициенты a_jk(p), b_jk(p), c_jk(p) являются полиномами оператора p:

Полученная операторная форма записи позволяет воспользоваться матричным представлением системы дифференциальных уравнений общего вида:

A(p)y = B(p) g + C(p) f, (1)

в котором

где  - число искомых функций y(t) равно числу дифференциальных уравнений;

m, r  число известных функций g(t) и f(t) соответственно, при этом наибольший порядок полиномов b_jk(p), c_jk(p) не должен превосходить старшего порядка n полиномов a_jk(p).

Полином |A| называется характеристическим полиномом системы (1).

Способ решения системы линейных дифференциальных уравнений (1) заключается в переходе от исходного выражения общего вида (1) к нормальной форме Коши и последующему интегрированию полученной системы уравнений первого порядка любым численным методом, например, методом Эйлера или Рунге-Кутта.

Для получения нормальной формы Коши представим матрицы А, В и С в виде:

A = A_npⁿ + A_n-1p^n-1 +…+A₁p + A₀;

B = B_npⁿ + B_n-1p^n-1 +…+B₁p + B₀;

C = C_npⁿ + C_n-1p^n-1 +…+C₁p + C₀,

где

причем A_n0.

Теперь, переписав (1) в виде

(A_npⁿ +…+A₁p +A₀)y = (B_npⁿ +…+B₁p +B₀)g + (C_npⁿ +…+C₁p + C₀)f,

раскрыв скобки и перейдя к оригиналам, получим выражение

A_ny⁽ⁿ⁾+A_n-1y^(n-1)+…+A₁y⁽¹⁾+A₀y = B_ng⁽ⁿ⁾+…+B₀g + C_nf⁽ⁿ⁾+…+C₀f, (2)

совпадающее по форме с традиционной скалярной записью дифференциальных уравнений, однако коэффициенты А_(), В_(), С_() и функции g, f и y в нем  суть матрицы.

Представив (2) в виде

0 = A_ny⁽ⁿ⁾+A_n-1y^(n-1)+…+A₁y⁽¹⁾+A₀y - B_ng⁽ⁿ⁾-…-B₀g - C_nf⁽ⁿ⁾-…-C₀f

и используя процедуру понижения порядка, введем n новых переменных х₁,х₂,…х_n, которые также будут являться матрицами (векторами)

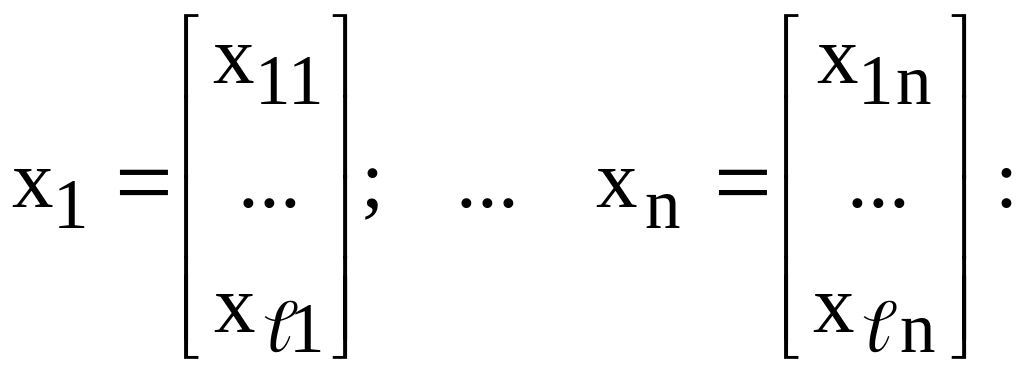
x₁ = A_ny^(n-1)+A_n-1y^(n-2)+…+A₂y⁽¹⁾+A₁y - B_ng^(n-1)-…-B₁g - C_nf^(n-1)-…-C₁f;

x₂ = A_ny^(n-2)+A_n-1y^(n-3)+…+A₃y⁽¹⁾+A₂y - B_ng^(n-2)-…-B₂g - C_nf^(n-2)-…-C₂f;

……..

x_n = A_ny - B_ng - C_nf.

Переписав полученные уравнения с учетом введенных переменных

и учитывая, что

можно выразить переменные в явном виде:

Полученная система уравнений является искомой нормальной формой Коши общего вида

(3)

в котором

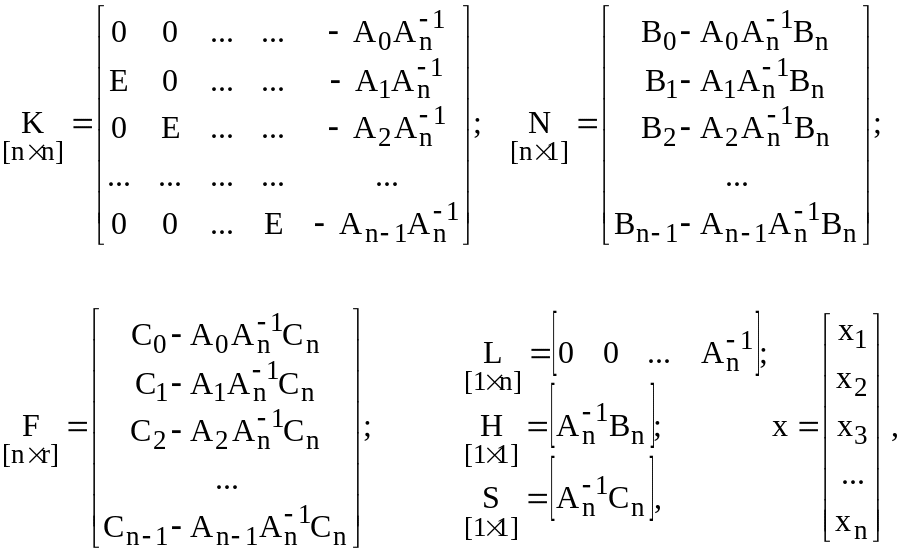
Е  единичная матрица размером .

Для решения нормальной системы можно воспользоваться методом Эйлера:

y_i = Lx_i + Hg_i + Sf_i;

x_i+1 = x_i + h(Kx_i + Ng_i + Ff_i),

где h  шаг интегрирования по переменной t.

Пример задания.

Задана структурная схема многомерной системы автоматического регулирования (рис. 4.1) с двумя задающими (входными) воздействиями g₁ и g₂, двумя регулируемыми (выходными) величинами y₁, y₂ и возмущением f.

Составить дифференциальные уравнения, устанавливающие взаимосвязь выходных величин y₁, y₂ с внешними воздействиями g₁, g₂, f.

Решить полученные дифференциальные уравнения относительно y₁(t) и y₂(t) при ступенчатом изменении g₁(t), g₂(t) и f(t).

Параметры передаточных функций: k₁=3; k₂=20; k₃=2; T₃=3; k₄=2.

Решение.

Используя заданную структурную схему и известные передаточные функции сначала составим математическую модель системы в изображениях по Лапласу. В соответствии со структурной схемой рис.1 выпишем уравнения связи:

y₁ = W₁₁u₁ – W_ff;

u₁ = g₁  y₁;

y₂ = W₂₁u₁ + W₂₂u₂;

u₂ = g₂ – y₂.

Подставляя величины u₁ и u₂ в выражения для y₁ и y₂ получим:

Раскроем выражения для передаточных функций:

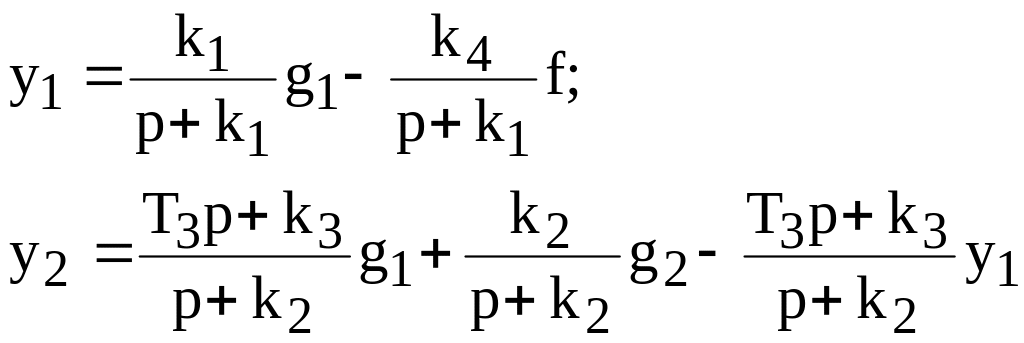
и избавимся от знаменателей:

(p + k₁)y₁ = k₁g₁ – k₄f;

(T₃p + k₃)y₁ + (p + k₂)y₂ = (T₃p + k₃)g₁ + k₂g₂.

Полученные уравнения представляют собою не что иное, как уравнения общего вида (1):

A(p)y = B(p) g + C(p) f,

в котором

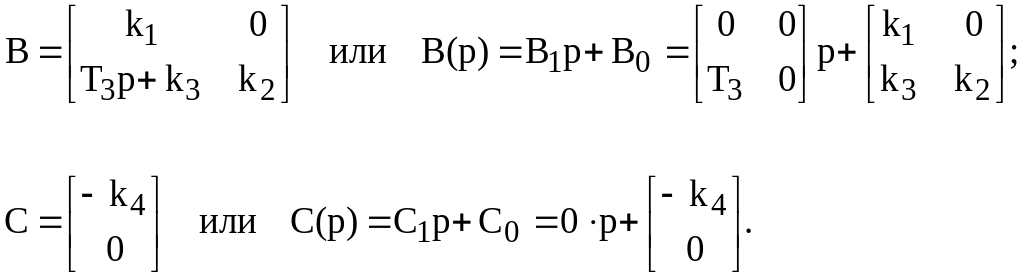
Для получения нормальной формы Коши

осталось определить матрицы K, N, F, L, H и S. Учитывая, что n=1, =2, r=1, вычислим:

Характеристическое уравнение |A|=0:

p² +(k₁ + k₂)p +k₁k₂ = 0

для заданных числовых параметров имеет вид

p² +(3 + 20)p +320 = p² +23p + 60 = 0,

и отрицательные вещественные корни

,

из чего следует, что решение будет устойчивым.

По известным матрицам K, N, F, L, H и S составляем описание системы регулирования в нормальной форме Коши:

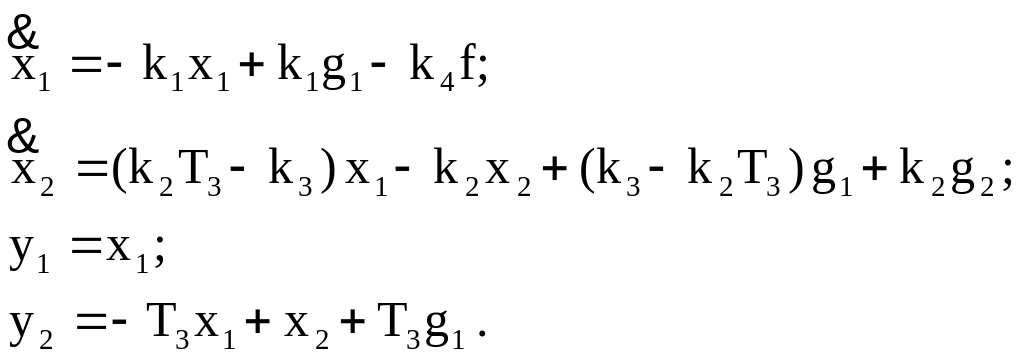
Для численного решения полученной системы воспользуемся уравнениями Эйлера

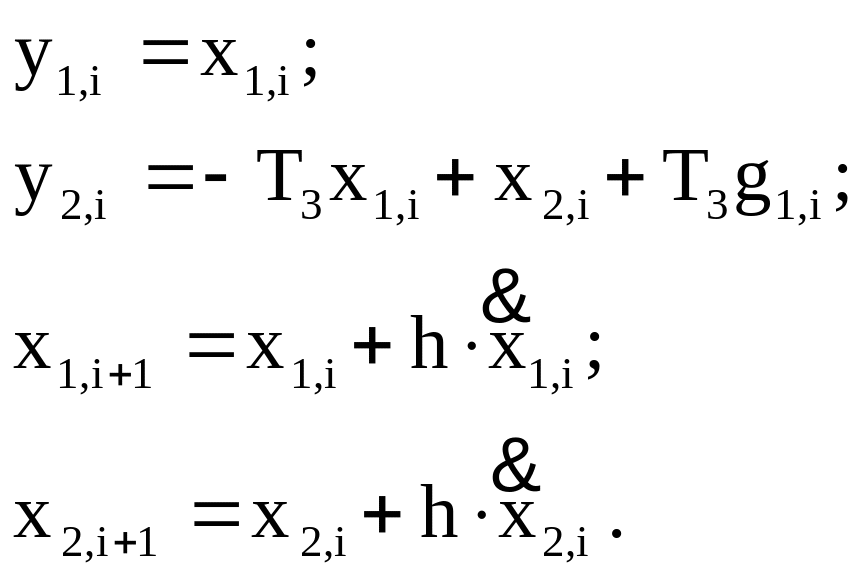
С оставленная на основе этих уравнений программа представлена ниже.

Результаты решения.

Целью решения полученных дифференциальных уравнений является изучение реакции выходных величин y₁(t), y₂(t) системы автоматического регулирования на единичные ступенчатые воздействия g₁(t), g₂(t), f(t).Для наглядного представления результатов следует рассмотреть три решения  отдельно для каждого внешнего воздействия: g₁(t)=1₀(t), g₂(t)=0, f(t)=0, (рис. 4.2а); g₁(t)=0, g₂(t)=1₀(t), f(t)=0, (рис.2б); g₁(t)=0, g₂(t)=0, f(t)= 1₀(t), (рис. 4.2в).

Р ассмотрение кривых переходных процессов на рис. 4.2 раскрывает характерную особенность многомерных систем автоматического регулирования  существование влияния какого-либо из внешних воздействий одновременно на несколько регулируемых величин (рис. 4.2а и 4.2в).

При синтезе систем, как правило, необходимо обеспечить независимость управления каждой выходной величиной так, как это получилось на рис. 4.2б.

Варианты заданий.

Для заданных вариантов многомерных систем автоматического регулирования, представленных ниже структурными схемами, составить математическую модель в виде системы дифференциальных уравнений, устанавливающих взаимосвязь выходных величин y₁(t), y₂(t) с внешними воздействиями g₁(t), g₂(t) и f(t). Решить полученные дифференциальные уравнения относительно y₁(t), y₂(t) поочередно задаваясь ступенчатым изменением внешних воздействий. Получить графическую иллюстрацию решения.

Указание.

При составлении математической модели рекомендуется на предварительных этапах расчетов убедиться в устойчивости искомого решения, определив для этого корни характеристического уравнения |A|=0. С этой же целью полезно найти собственные числа матрицы K, решив для этого уравнение |pE-K|=0. Корни полинома |A| и собственные числа матрицы K должны совпадать.

Дополнительные вопросы.

1. Метод Рунге-Кутта решения дифференциальных уравнений.

2. Метод Адамса решения дифференциальных уравнений.

3. Метод Эйлера решения дифференциальных уравнений.

4. Метод Милна решения дифференциальных уравнений.

5. Метод малого параметра решения дифференциальных уравнений.