2. Условный экстремум. Метод множителей Лагранжа

Теоретические сведения

Пусть требуется найти экстремум функции n переменных f(x₁,x₂,…,x_n) при условии, что переменные x₁,x₂,…,x_n связаны соотношениями (ограничениями)

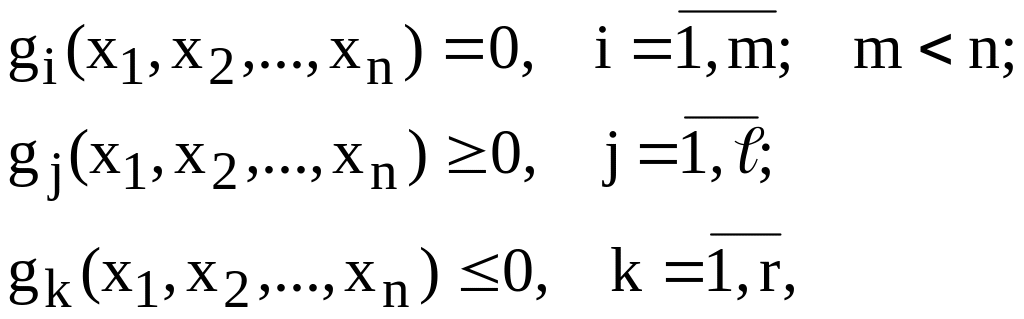
среди которых количество m ограничений-равенств меньше числа n переменных, а количество  и r ограничений-неравенств может быть произвольным.

Для нахождения значений {x₁,x₂,…,x_n}=Х, необходимо доставляющих экстремумы функции f(X), можно воспользоваться методом неопределенных множителей Лагранжа:

1. Ограничения-неравенства g(X)0 приводятся к виду (Х)0, где (Х) = - g(X).

2. Полученные ограничения-неравенства

в свою очередь приводятся к ограничениям-равенствам путем введения +r дополнительных переменных

В результате задача поиска условного экстремума примет канонический вид:

в котором соотношение m++r < n++r указывает на возможность получения множества допустимых решений, а значит, и нахождения среди них тех, которые доставляют экстремум f(X).

3. Составляется функция Лагранжа:

Ф(x₁,…,x_n,₁,…,_m++r) = f(x₁,x₂,…,x_n)+₁q₁+₂q₂+…+_m++rq_m++r ,

в которой дополнительные переменные {₁,…,_m++r}= называются неопределенными множителями Лагранжа.

Для составленной функции Лагранжа можно ставить задачу нахождения безусловного экстремума

Ф(Х,)  extr,

результат решения которой будет совпадать с искомым решением исходной задачи нахождения условного экстремума.

4. Для функции Ф(Х,) составляются необходимые условия существования экстремума:

Ф(Х,)=0

или

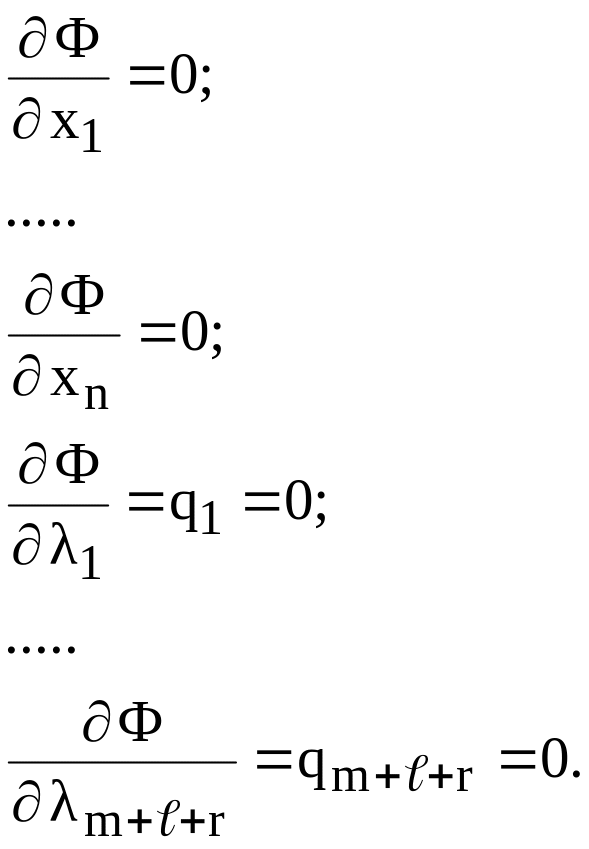
5. Полученную систему уравнений Ф(Х,)=0 решают, и в результате решения находят значения

,

удовлетворяющие необходимым условиям существования экстремума.

6. Для решения вопроса о том, существует ли в найденных точках максимумы или минимумы следует воспользоваться достаточными условиями существования экстремумов, которые для гладких функций Ф() формулируются следующим образом:

если в некоторой точке матрица вторых производных положительно определена, то в анализируемой точке лежит минимум функции f(Х);

если отрицательно определена  максимум.

Если Ф(Х,) негладкая, то можно использовать достаточные условия вида, например, для максимума:

Ф(Х,*)  Ф(Х*,*) = Ф(Х*,),

однако проверка этих условий при большом числе переменных трудоемко, и при решении практических задач вопрос о наличии минимума или максимума решается на основании дополнительных соображений, вытекающих из содержания задачи.

Пример задания.

Найти состав продуктов наименьшей стоимости, обеспечивающий недельную потребность человека в белках, жирах и углеводах.

Числовые данные к задаче представлены в таблице.

Продукт	Содержание белков, о.е.	Содержание жиров, о.е.	Содержание углеводов, отн. единиц	Цена за1 кг
Хлеб	0,07	0,01	0,5	10
Масло	0,06	0,8	0,09	60
Недельная потребность, кг	0,6	0,7	2,5

Решение.

Обозначим через х₁ и х₂ массы хлеба и масла, составляющие искомый состав продуктов. В качестве целевой функции f(x₁,x₂) возьмем суммарную стоимость продуктов: f(x₁,x₂) = 10х₁ + 60х₂. Недельную потребность в белках, жирах и углеводах примем за ограничения, накладываемые на переменные х₁ и х₂.

В указанной постановке решаемая задача может быть сформулирована как задача поиска условного экстремума:

10х₁ + 60х₂  min;

0,07х₁ + 0,06х₂  0,6;

0,01х₁ + 0,8х₂  0,7;

0,5х₁ + 0,09х₂  2,5;

х₁0;

х₂0.

Решим задачу методом множителей Лагранжа.

1. Приведем ограничения к виду (Х)  0:

0,6 - 0,07х₁ - 0,06х₂  0;

0,7 - 0,01х₁ - 0,8х₂  0;

2,5 - 0,5х₁ - 0,09х₂  0;

-х₁0;

-х₂0.

2. Путем ведения дополнительных переменных х₃,х₄,х₅,х₆,х₇ перейдем к ограничениям-равенствам:

0,6 - 0,07х₁ - 0,06х₂ + х₃² = 0;

0,7 - 0,01х₁ - 0,8х₂ +х₄² = 0;

2,5 - 0,5х₁ - 0,09х₂ +х₅² = 0;

-х₁ + х₆² = 0;

-х₂ + х₇² = 0.

3. Сформируем функцию Лагранжа:

Ф(х₁,х₂,х₃,х₄,х₅,х₆,х₇,₁,₂,₃,₄,₅) =

= 10х₁ + 60х₂ +₁(0,6 - 0,07х₁ - 0,06х₂ + х₃²) +

+₂(0,7 - 0,01х₁ - 0,8х₂ +х₄²)+

+₃(2,5 - 0,5х₁ - 0,09х₂ +х₅²)+

+₄(-х₁ + х₆²)+

+₅(-х₂ + х₇²).

4. Составим необходимые условия Ф(Х,)=0:

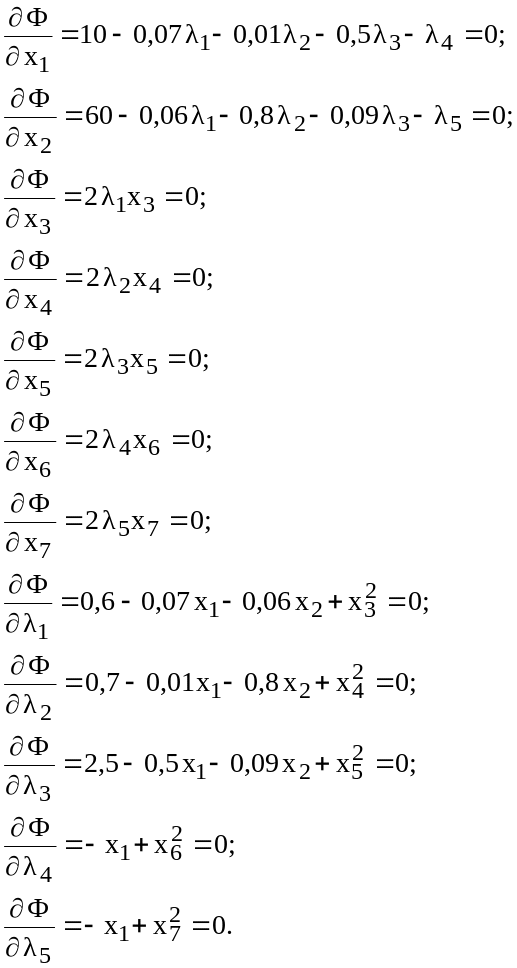
5. Решить полученную систему нелинейных уравнений можно каким-либо формальным методом с помощью, например, средств математического пакета Mathcad:

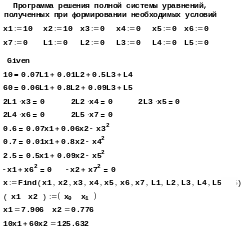
В результате использования приведенной программы с различными начальными условиями было получено четыре решения:

х₁ = 70; х₂ = 0; f₁(х₁,х₂) = 700;

х₁ = 7,906; х₂ = 0,776; f₂(х₁,х₂) = 125,63;

х₁ = 4,051; х₂ = 5,274; f₃(х₁,х₂) = 356,96;

х₁ = 0; х₂ = 27,778; f₄(х₁,х₂) = 1666,68.

Лучшим решением из приведенного перечня является второе.

Необходимо отметить, что значительный размер сформированной системы уравнений, полученных из необходимых условий (12 уравнений), вызван:

во-первых, тем, что переход от ограничений-неравенств к ограничениям-равенствам осуществляется путем введения дополнительных переменных х₃,х₄,х₅,х₆,х₇, число которых равно числу ограничений-неравенств;

во-вторых, тем, что переход от задачи нахождения условного экстремума к задаче безусловного поиска возможен, в соответствии с методом Лагранжа, с помощью введения дополнительных переменных ₁,₂,₃,₄,₅, число которых равно общему числу ограничений задачи.

Таким образом, решение задачи методом Лагранжа получено ценой повышения ее размерности. Этот недостаток ограничивает область применения метода Лагранжа сравнительно простыми задачами, поэтому с повышением числа переменных и ограничений целесообразно переходить к численным методам математического программирования.

Анализ решения.

Для проверки правильности полученных результатов и осмысления содержательной стороны решаемой задачи поиска условного экстремума проведем ее анализ.

Переписав исходную систему ограничений-неравенств в виде

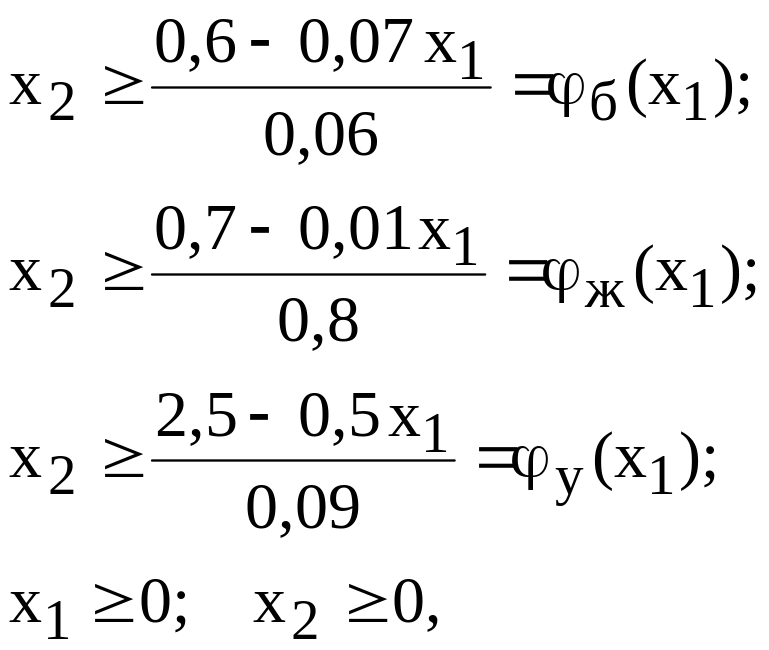
получаем возможность графически представить эти ограничения на плоскости х₂ох₁ в виде прямых _б(х₁); _ж(х₁); _у(х₁); х₂=0; х₁=0, снабдив их штриховкой, направленной в сторону области допустимых значений х₁ и х₂, рис. 2.1,2,2.

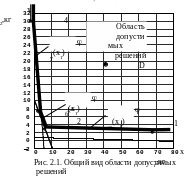
Как следует из рис. 2.1, область допустимых решений не является замкнутой, допустимые значений х₁ и х₂ не ограничены сверху и любая пара их допустимых значений, например, точка D, обеспечивает необходимую потребность в белках, жирах и углеводах с избытком.

Поскольку целью задачи является нахождение минимума затрат, пропорциональных массам х₁ и х₂, очевидно, что искомое решение будет лежать на границе области допустимых решений, составленной отрезками 1-2-3-4, ограничивающей значения х₁ и х₂ снизу.

При этом решения на интервале [1-2) обеспечивают точное выполнение потребности в жирах (0,7кг) и избыток белков и углеводов;

на интервале (2-3)  точное обеспечение потребности в белках (0,6кг) и избыток жиров и углеводов;

на интервале (3-4]  точное обеспечение потребности в углеводах (2,5кг) при избытке белков и жиров.

В смежных точках 2 и 3 активно по два ограничения:

в точке 2  строгое выполнение условия по белкам и жирам при избытке углеводов;

в точке 3  строгое выполнение условий по белкам и углеводам при избытке жиров.

Чтобы ответить на вопрос, в какой же точке ломаной 1-2-3-4 расположен минимум функции f(x₁,x₂) =10x₁+60x₂, построим проекции линий равного уровня f(x₁,x₂) = 20, f₂(x₁,x₂)=125,63 и f₃(x₁,x₂)=356,96 на плоскость х₂ох₁, т.е. построим в этой плоскости прямые

10x₁+60x₂=20;

10x₁+60x₂=125,63 ;

10x₁+60x₂=356,96,

две из которых, как и следовало ожидать из результатов аналитического решения, проходят через точки 2 и 3, рис. 2.2.

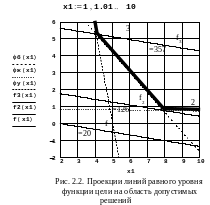
Взаимное расположение построенных линий f(x₁,x₂), f₂(x₁,x₂), f₃(x₁,x₂) и границы 1-2-3-4 показывает, что всякая линия уровня со значением f(x₁,x₂)<126 располагается ниже прямой f₂(x₁,x₂) и, следовательно, не будет иметь общих точек с границей 1-2-3-4, т.е. решение задачи со значением f(x₁,x₂), меньшим, чем f₂(x₁,x₂), не существует, и в точке 2 находится искомый условный минимум.

Найденное решение, как это было установлено выше, обеспечивает избыток углеводов, но, тем не менее, это лучшее решение при данных условиях. Если провести линию уровня через любую другую точку ломаной 1-2-3-4, то можно убедиться, что она будет соответствовать значению f(x₁,x₂)>126, т.е. в точке 2 располагается единственный условный минимум задачи.

Неактивность в окрестностях экстремума ограничений х₁0, x₂0 свидетельствует о том, что эти условия при составлении функции Лагранжа можно было исключить и значительно понизить размерность задачи.

Кроме того, проведенный анализ показывает, что экстремум в данной задаче можно было найти более рациональным способом  решить систему двух уравнений, составляющих ограничения по белкам и жирам:

0,07х₁ + 0,06х₂ = 0,6;

0,01х₁ + 0,8х₂ = 0,7.

Р ешение этой системы и поверка граничных условий представлены в программе:

Проверка показывает полное совпадение результатов с решением по методу Лагранжа, а также подтверждает ожидаемое строгое выполнение условий по белкам (0,6 кг) и жирам (0,7 кг) с избытком углеводов (4,652 > 2,5 кг).

Варианты заданий.

1. Определить размеры x,y,z каркаса заданной конструкции (рис. 2.3а), обеспечивающие максимальное значение его объема, если длина рейки, отпущенной на его изготовление, равна 30 метрам. Провести анализ полученного решения.

2.Определить диаметр и высоту цилиндрического бака с крышкой объемом 8 м³, обеспечивающие минимальный расход материала на его изготовление. Провести анализ полученного решения.

3. Составить план выпуска изделий, обеспечивающий максимальную прибыль от их реализации. Провести анализ решения.

Исходные данные представлены в таблице.

Вид сырья	Количество сырья, идущего на единицу изделия		Запас сырья
	Плита	Перемычка
Песок	7	5	70
Щебень	9	4	80
Цемент	2	2	30
Прибыль от единицы изделия	30	19

4. Имеются два предприятия и две базы, снабжающие предприятия сырьем. Потребности предприятий в сырье равны p₁ и p₂. Запасы сырья на базах b₁ и b₂, причем b₁+ b₂ > p₁+ p₂. Стоимость перевозки единицы сырья с i-й базы на j-е предприятие составляет с_ij (рис. 2.3б).

Найти план снабжения предприятий сырьем с минимальными затратами на перевозку. Провести анализ полученного решения.

Числовыми данными задачи задаться самостоятельно.

5. Предприятие производит два вида изделий. Для каждого изделия требуется два вида сырья в известном количестве а_ij,i=1,2; j=1,2. Запасы сырья равны S₁ и S₂. Прибыль от каждого изделия p₁ и p₂. Задан обязательный заказ на каждое изделие z₁ и z₂.

Найти план выпуска изделий, обеспечивающий максимальную прибыль от их реализации при условии выполнения обязательного заказа. Провести анализ полученного решения.

Числовыми данными задаться самостоятельно.

6. Четыре станка обрабатывают два вида деталей: А и В. Каждая деталь проходит обработку на всех четырех станках.

Известны: время обработки детали на каждом станке, время работы станков в течение одного цикла производства и прибыль, получаемая от выпуска одной детали каждого вида.

Эти данные приведены в таблице:

Станки	Время обработки одной детали,ч.		Время работы станка за один
	А	В	цикл производства, ч.
I	1	2	16
II	2	3	25
III	1	1	10
IV	3	1	24
Прибыль на одну деталь, усл.ден.ед.	4	1	-

Составить план производства, обеспечивающий наибольшую прибыль. Провести анализ полученного решения.

7. Для изготовления 3-х видов изделий A, B, C используется токарное, фрезерное, сварочное и шлифовальное оборудование.

Затраты времени на обработку одного изделия для каждого из типов оборудования указанны в таблице. В ней же указан общий фонд рабочего времени, а так же прибыль от реализации одного изделия каждого вида:

Тип оборудования	Затраты времени (станко-ч.) на обработку 1-го вида изделия			Общий фонд рабочего
	A	B	C	времени (ч).
Фрезерное Токарное Сварочное Шлифовальное	2 1 7 4	4 8 4 6	5 6 5 7	120 280 240 360
Прибыль	10	14	12

Требуется определить сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной. Провести анализ полученного решения.

8. Продукцией городского молочного завода является молоко, кефир и сметана, расфасованные в бутылки. На производство 1т молока, кефира и сметаны требуется соответственно 1010, 1010 и 9450 кг молока. При этом затраты рабочего времени при разливе 1т молока и кефира составляют 0.18 и 0.19 машино-часов. На расфасовке 1т сметаны заняты специальные автоматы в течение 3.25 ч. Всего для производства цельномолочной продукции завод может использовать 136 000 кг молока. Основное оборудование может быть занято в течение 21.4 машино-часов, а автоматы по расфасовке сметаны в течение 16.25 ч. Прибыль от реализации 1т молока, кефира и сметаны соответственно равна 30, 22 и 136 усл. ден. ед. Завод должен ежедневно производить не менее 100т молока, расфасованного в бутылки. На производство другой продукции не имеется никаких ограничений.

Требуется определить, какую продукцию и в каком количестве следует ежедневно изготовлять заводу, чтобы прибыль от ее реализации была максимальной. Провести анализ полученного решения.

9. Кондитерская фабрика для производства трех видов карамели А,В,C используют три вида основного сырья: сахарный песок, патоку, фруктовое пюре. Нормы расхода сырья каждого вида на производство 1тонны карамели в таблице. В ней же указано общее количество сырья каждого вида, которое может быть использовано фабрикой, а также приведена прибыль от реализации 1тонны карамели данного вида:

Вид сырья	Нормы расхода сырья (т) на 1 т карамели			Общее количество сырья (т)
	А	В	С
Сахарный песок	0,8	0,5	0,6	800
Патока	0,8	0,4	0,3	600
Фруктовое пюре	-	0,1	0,1	120
Прибыль от реализации 1т продукции (усл.ден.ед.)	108	112	126

Найти план производства карамели, обеспечивающей максимальную прибыль от ее реализации. Провести анализ полученного решения.

10. На мебельной фабрике из стандартных листов фанеры необходимо вырезать заготовки трёх видов в количествах, соответственно равных 24, 31 и 18 шт. Каждый лист фанеры может быть разрезан на заготовки двумя способами. Количество получаемых заготовок при данном способе раскроя приведено в таблице. В ней же указана величина отходов, которые получены при данном способе раскроя одного листа фанеры:

Вид заготовки	Количество заготовок при раскрое по способу
	I	II
1	2	6
2	5	4
3	2	3
Величина отходов (см2)	12	16

Определить, сколько листов фанеры и по какому способу следует раскроить так, чтобы было получено не меньше нужного количества заготовок при минимальных отходах. Провести анализ полученного решения.

11. На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество корма каждого вида, которое должны ежедневно получать лисицы и песцы, приведено в таблице. В ней же указано общее количество корма каждого вида, которое может быть использовано зверофермой и прибыль от реализации одной шкурки лисицы и песца.

Вид корма	Количество единиц корма, которое ежедневно должны получать		Общее количество корма
	лисица	песец
I	2	3	180
II	4	1	240
III	6	7	426
Прибыль от реализации одной шкурки (усл. ден.ед.)	16	12

Определить сколько лисиц и песцов следует выращивать на звероферме, чтобы прибыль от реализации их шкур была максимальной. Провести анализ полученного решения.

12. Для перевозок груза на трех линиях могут быть использованы суда трех типов. Производительность судов при использовании их на различных линиях характеризуется данными, приведенными в таблице. В ней же указаны общее время, в течение которого суда каждого типа находятся в эксплуатации, и минимально необходимые объемы перевозок на каждой из линий:

Тип судна	Производительность судов (млн. тонно-миль в сутки)на линии			Общее время эксплуатации
	1	2	3	судов (сут.).
I	8	14	11	300
II	6	15	13	300
III	12	12	4	300
Заданный объем перевозок (млн. тонно-миль)	3000	5400	3300	-

Определите, какие суда, на какой линии и в течение какого времени следует использовать, чтобы обеспечить максимальную загрузку судов с учетом возможного времени их эксплуатации. Провести анализ полученного решения.

13. Для обогрева помещений используют четыре агрегата, каждый из которых может работать на любом из пяти сортов топлива, имеющемся в количествах 90,110,70,80 и 150 т. Потребность в топливе каждого из агрегатов соответственно равна 80,120,140 и 160 т. Теплотворная способность i-го сорта топлива при использовании его на j-м агрегате задается матрицей

(с_ij) =

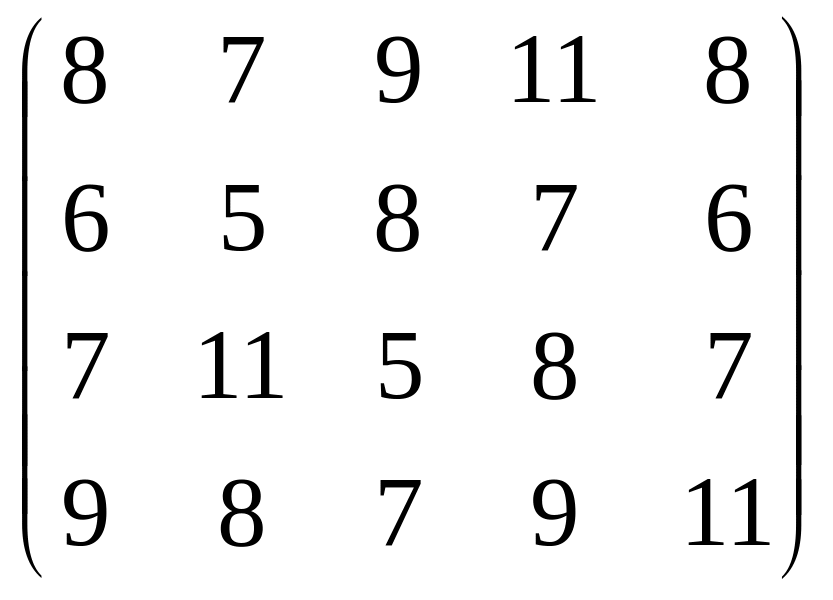
Найти такое распределение топлива между агрегатами, при котором получается максимальное количество теплоты от использования всего топлива. Провести анализ полученного решения.

14. Изготовляемый на пяти кирпичных заводах кирпич поступает на шесть строящихся объектов. Ежедневное производство кирпича и потребность в нём указаны в таблице. В ней же указана цена перевозки 1000 шт. кирпича с каждого из заводов к каждому из объектов:

Кирпичный	Цена перевозки 1 тысячи штук кирпича строящемуся объекту						Производ- ство кирпича
завод	1	2	3	4	5	6	(тыс.шт.)
1	8	7	5	10	12	8	240
2	13	8	10	7	6	13	360
3	12	4	11	9	10	11	180
4	14	6	12	13	7	14	120
5	9	12	14	15	8	13	150
Потребность в кирпиче (тыс.шт)	230	220	130	170	190	110

Составить план перевозок, согласно которому обеспечиваются потребности в кирпиче на каждом из строящихся объектов при минимальной общей стоимости перевозок. Провести анализ полученного решения.

15. При производстве 4 видов кабеля выполняются 5 групп технологических операций. Нормы затрат на 1 км кабеля данного вида на каждый из групп операций, прибыль от реализации 1 км каждого вида кабеля , а также общий фонд рабочего времени, в течение которого могут выполняться эти операции. Данные представлены в таблице:

Технологические операции	Нормы затрат времени (ч) на обработку 1км кабеля вида				Общий фонд раб.времени(ч)
Волочение	1,2	1,8	1,6	2,4	7200
Наложение изоляции	1,0	0,4	0,8	0,7	5600
Скручивание элементов в кабель	6,4	5,6	6,0	8,0	11176
Освинцование	3,0		1,8	2,4	3600
Испыт. и контроль	2,1	1,5	0,8	3,0	4200
Прибыль от реализации 1 км кабеля (усл. ден. ед.)	1,2	0,8	1,0	1,3

Определить такой план выпуска кабеля, при котором общая прибыль от реализации изготовляемой продукции являлась максимальной. Провести анализ полученного решения.

16. Метод наименьших квадратов.

17. Наибольшее и наименьшее значения функции в заданной области.

18. Скалярные и векторные поля.

19. Формула Тейлора для функций двух переменных.

20. Кривизна поверхностей.