1. Многочлены и их корни

Теоретические сведения

Функция

P(x) = a_nxⁿ + a_n-1x^n-1 + …+a₁x + a₀,

где n - целое число, называется многочленом от x степени n.

Число  называется корнем многочлена P(x), если Р()=0, иначе говоря   корень уравнения Р(х)=0.

Уравнение Р(х)=0, в котором Р(х)  многочлен степени n, называется алгебраическим уравнением степени n.

Всякое алгебраическое уравнение Р(х)=0 степени n имеет по крайней мере один корень (основная теорема алгебры) и не более n различных корней.

Остаток от деления многочлена Р(х) на разность (х-) равен Р(), т.е. значению Р(х) при х= (теорема Безу).

Если   корень многочлена Р(х) степени n, то этот многочлен делится на (х-) без остатка, т.е. представляется в виде произведения

Р(х) = (х - )Q(х),

где Q(х)  многочлен степени n-1.

Всякий многочлен n-й степени разлагается на n линейных сомножителей (х-₁),…,(х-_n), где ₁,…,_n  корни многочлена, и множитель, равный коэффициенту при хⁿ:

a_nxⁿ + a_n-1x^n-1 + …+a₁x + a₀ = a_n (х-₁)  (х-₂)… (х-_n),

причем часть или даже все корни  могут быть одинаковыми. Такие корни называются кратными.

Приравнивая в последнем уравнении коэффициенты при равных степенях х, получим выражения, связывающие коэффициенты многочлена с его корнями:

a_n-1 = -a_n(₁ + ₂ + … +_n);

a_n-2 = a_n(₁₂ + ₁₃ + … +_n-1 _n);

…………

a₀ = a_n(₁₂ … _n)(-1)ⁿ.

Эти выражения называются формулами Виета.

Пример задания.

Для дифференциального уравнения

в плоскости его коэффициентов А и В найти область, соответствующую устойчивому решению y(t), выделив в ней подобласти с различным характером поведения решения при изменении аргумента t.

Решение.

Для анализа устойчивости решения y(t) дифференциального уравнения

составим характеристическое уравнение

s³+As²+Bs+1=0,

корни которого обозначим через s₁,s₂,s₃.

В соответствии с определением устойчивости по Ляпунову устойчивое решение y(t) будет получено, если все корни s₁,s₂ и s₃ будут иметь отрицательные вещественные части, т.е. будут располагаться слева от мнимой оси комплексной плоскости s=j.

Характер устойчивого решения y(t) зависит от взаимного расположения корней характеристического уравнения. Для рассматриваемого уравнения с тремя корнями возможны следующие основные варианты их взаимного расположения, рис.1.1:

1  все корни вещественные: -₁; -₂; -₃;

2  два корня комплексно-сопряженные и один вещественный: -₁; -₂; причем ₁<₂;

3  два корня комплексно-сопряженные и один вещественный: -₁; -₂; причем ₁>₂;

4 – комплексные корни имеют положительную вещественную часть: -₁; ₂ (неустойчивое решение).

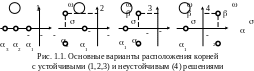
Д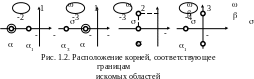 ля выделения в плоскости ВоА указанных подобластей 1,2,3 и 4 необходимо найти расположения корней, соответствующие границам 1-2, 1-3, 2-3 между этими подобластями, а также общую границу 3-4 устойчивого решения, рис.1.2.

Взаимосвязь корней с коэффициентами А и В определим по формулам Виета:

А = -(s₁+s₂+s₃); B = (s₁s₂+s₁s₃+s₂s₃); 1 = -s₁s₂s₃.

Подставляя вместо s₁,s₂,s₃ выражения для корней, соответствующие искомым границам получим уравнения для этих границ в плоскости ВоА в параметрическом виде.

Для границы 1-2:

корни s₁ = -₁; s₂ = s₃ = -; _1;

коэффициенты A=₁+2;

B=2₁+²;

1=₁², где [).

Построить эту границу можно, изменяя  от 1 до . При этом будет обеспечено условие ₁.

Для границы 1-3:

корни s₁ = s₂ = -; s₃ = -₃; ₃;

коэффициенты A=₃+2;

B=2₃+²;

1=₃², где (01].

Выполнение условия ₃ будет обеспечено при изменении  в интервале от 0 до 1.

Для границы 2-3:

корни s₁ = -; s_2,3 = -j;

коэффициенты A=-((- )+(-+j)+(--j))=3;

B=(-)(-+j)+(-)(--j)+(-+j)(--j)=3²+²;

1=-(- )(-+j)(--j)=(²+²), где (01].

Для границы 3-4:

корни s₁ = -₁; s_2,3 = j;

коэффициенты A=-((-₁ )+(j)+(-j))=₁;

B=(-₁)(j)+(-₁)(-j)+(j)(-j)=²; 1=-(-₁ )(j)(-j)=₁²,

где (0).

Примечание.

Выражения для искомых границ в данной задаче могут быть получены в явном виде В(А), однако параметрический вид решения обладает большей общностью и может быть распространен для задач анализа уравнений с более высоким порядком.

Программа вычисления А и В для каждой из указанных границ в пакете Mathcad представлена ниже.

В программе величинами А12,В12, А13,В13, А23,В23, А34,В34 обозначены коэффициенты А и В, образующие соответственно границы 1-2, 1-3, 2-3 и 3-4. Остальные обозначения в программе совпадают с аналитическими выражениями в тексте и к разночтениям не приводят.

Следует отметить, что представленный алгоритм может быть реализован на любом формальном языке; математический пакет Mathcad в данном случае выбран из-за его удобного графического интерфейса.

Результат решения.

Результат заданного разбиения пространства коэффициентов А и В представлен на рис. 1.3.

Нумерация областей совпадает с принятой на рис. 1.1. Области 1,2,3 соответствуют устойчивым решениям дифференциального уравнения, а область 4  неустойчивому.

Варианты заданий.

1. Для дифференциального уравнения

в плоскости его коэффициентов А и В найти область, соответствующую степени устойчивости = -0,3; выделив на ней подобласти с различным характером поведения решения y(t) при изменении аргумента t (рис. 1.4а).

2. Для дифференциального уравнения, указанного в варианте 1, в пространстве его коэффициентов А и В найти область, расположенную слева от мнимой оси комплексной плоскости корней характеристического уравнения внутри угла 45, выделив на ней подобласти с различным характером поведения решения y(t) при изменении аргумента t (рис. 1.4б).

Указание. Границы угла 45 могут быть описаны выражением s = -j.

3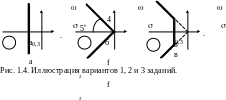 . Для дифференциального уравнения, указанного в варианте 1, в пространстве его коэффициентов А и В найти область, расположенную слева от мнимой оси комплексной плоскости корней характеристического уравнения внутри угла 45и обладающую степенью устойчивости =-0,3; выделив на ней

подобласти с различным характером поведения решения y(t)

4. Для дифференциального уравнения

в плоскости его коэффициентов А и В найти область, соответствующую устойчивому решению y(t), выделив в ней подобласти с различным характером поведения решения при изменении аргумента t. Указание: всего 6 подобластей.

5. Для дифференциального уравнения

в плоскости его коэффициентов А и В найти область, соответствующую устойчивому решению y(t), выделив в ней подобласти с различным характером поведения решения при изменении аргумента t.

6. Для системы, описываемой дифференциальным уравнением второго порядка

,

с корнями характеристического полинома s_1,2 = -j, найти аналитические выражения для y(t,k,,); периода колебаний Т(); максимального значения y(t), достигаемого в момент времени t=T/2; времени регулирования t_p (временем регулирования называется момент времени t_p, после которого выполняется условие

).

7. Для дифференциального уравнения

,

с корнями характеристического уравнения, представленными на рис. 1.1, 1.2, 1.3, в плоскости В0А (см. рис.3) построить линии равных значений наибольшей вещественной части  (линии равной степени устойчивости).

Указание. Для случая рис. 1.1 и 1.2 ₁=const; для случая рис.1.3 ₂=const; ₁,₂=(0;1).

8. Для дифференциального уравнения

,

с корнями характеристического уравнения, представленными на рис.1.1, 1.2, 1.3, в плоскости В0А (см. рис.3) построить линии равных значений для наименьших вещественных частей .

Указание. Для случая рис.1.1 ₃=const; для случая рис.1.2 ₂=const; для случая рис.1.3 ₁=const; =(0;).

9. Для дифференциального уравнения

,

с корнями характеристического уравнения, представленными на рис.1.1, 1.2, 1.3, в плоскости В0А (см. рис.3) построить линии равного уровня для отношения =/=const (линии равной колебательности).

Указание. Рассмотреть случаи рис.1.2 и 1.3; =(0;).

10. Для дифференциального уравнения

,

найти параметры А, В и корни s_1,2 = -j, обеспечивающие значение y(T/2)=1,05k (см. вариант задания 6).

11. Для дифференциального уравнения

найти А, В и С, а также значения корней s₁,s₂,s₃, обеспечивающие получение решения y(t) с наименьшим временем регулирования t_p (см. вариант задания 6).

12. Для объекта управления, заданного системой дифференциальных уравнений в нормальной форме Коши

,

где В – матрица размером 33 с произвольными элементами; N – матрица размером 31 с произвольными элементами; х – вектор переменных состояния х=[x₁ х₂ х₃]^Т, построить модальный регулятор R=[r₁ r₂ r₃], задавшись желаемым расположением корней характеристического полинома s₁ = -1,5; s_2,3 = -1j2,5.

Указание. Для расчёта регулятора использовать соотношение

|sE-B+NR|=s³+a₂s²+a₁s+a₀,

в правую часть которого подставляется полином с желаемым расположением корней; Е – единичная матрица.

13. Для объекта управления, заданного системой дифференциальных уравнений в нормальной форме Коши

,

где В – матрица размером 44 с произвольными элементами; N – матрица размером 41 с произвольными элементами; х – вектор переменных состояния х=[x₁ х₂ х₃ х₄]^Т, построить модальный регулятор R=[r₁ r₂ r₃ r₄], задавшись желаемым расположением корней характеристического полинома s_1,2 = -1,6j0,9; s_3,4 = -1j2,6.

14. Для объекта управления, заданного системой дифференциальных уравнений в нормальной форме Коши

,

где В – матрица размером 33 с произвольными элементами; N – матрица размером 32 с произвольными элементами; х – вектор переменных состояния х=[x₁ х₂ х₃]^Т, построить модальный регулятор

,

задавшись желаемым расположением корней характеристического полинома s₁ = -1,5; s_2,3 = -1j2,5 (модальное управление при наличии части переменных состояния).

15. Для объекта управления, заданного системой дифференциальных уравнений в нормальной форме Коши

,

где В – матрица размером 33 с произвольными элементами; N – матрица размером 31 с произвольными элементами; х – вектор переменных состояния х=[x₁ х₂ х₃]^Т, построить модальный регулятор R=[r₁ r₂ 0], задавшись желаемым расположением двух корней характеристического полинома s_2,3 = -1j2,5 (неполное модальное управление).

16. Методы нахождения корней многочленов высших степеней.

17. Методы решения задач векторной алгебры.

18. Приёмы вычисления значения определителя произвольного порядка.

19. Интерполяция функций (многочлены Чебышёва, сплайны).

20. Численное решение систем алгебраических уравнений.