Правая часть данного неоднородного уравнения имеет вид
,
в данном
случае
.Так
как число
+i =2 + i не является корнем характеристического уравнения, то частное решение будем искать в форме
Найдем производные :
Подставим выражения и производных в заданное уравнение, получим после приведения подобных членов
Сократим на
и приравняем коэффициенты при
и
,
получим два уравнения для определения
А и В:
,
откуда
Запишем частное решение
.Общее
решение будет иметь вид
.
Пример 5. Найти частное решение
линейного неоднородного уравнения,
удовлетворяющее начальным условиям.
.
Решение. Найдем вначале общее
решение, которое будет иметь вид
.
Чтобы найти общее решение соответствующего
однородного уравнения
,
составим характеристическое уравнение
и найдем его корни
Общее решение соответствующего однородного уравнения
.
Правая часть данного неоднородного уравнения имеет вид
,
в данном
случае
.Так
как число +i
= i не является корнем
характеристического уравнения, то
частное решение будем искать в форме
Подставим выражения и производных в заданное уравнение, получим после приведения подобных членов
Приравняем
коэффициенты при
и
,
получим два уравнения для определения
А и В:
,
откуда
Следовательно, частное решение
.Общее
решение будет иметь вид
.
Найдем С1, С2, используя начальные условия
или
Отсюда С1=1, С2=0. Искомое частное решение будет
.
Задачи для самостоятельного решения
В задачах 1-8 для каждого из данных уравнений написать частное решение с неопределенными коэффициентами (числовых значений коэффициентов не находить)
1.
5.
2.
6.
3.
7.
4.
8.
Решить уравнения
9.
Ответ:.
.
10.
Ответ:
11.
Ответ:
12.
Ответ:
13.
Ответ:
14.
Ответ:
Занятие 8. Системы дифференциальных уравнений
Линейные системы дифференциальных уравнений можно решать методом исключения.
Для нахождения решения нормальной системы двух дифференциальных уравнений первого порядка, т.е. системы вида
(1)
разрешенной относительно производных от искомых функций y и z, дифференцируем по х одно из них
(2)
Определяя z из первого уравнения системы (1) и подставляя найденное выражение
(3)
в уравнение (2), получаем уравнение второго порядка с одной неизвестной функцией у. Решая его, находим
,
(4)
где
и
- произвольные постоянные. Подставляя
(4) в формулу (3), определяем функцию z.
Совокупность формул (3) и (4), где у
заменено на
,
дает общее решение системы.
Пример 1. Решить систему
Решение. Дифференцируем первое уравнение по х.
.
Из первого уравнения определяем z:
.
Из второго уравнения находим
Подставляя z и
в уравнение, полученное после
дифференцирования, приходим к уравнению
второго порядка с одной неизвестной у:
Это неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами и правой частью специального вида. Решим его
,
,
,
следовательно,
.
Частное решение будем искать в виде
.
Найдем неизвестные коэффициенты
;
.
Подставляя в уравнение, получим
;
;
Таким образом,
.
Общее решение
.
Тогда
=
.
Таким образом, решение исходной системы
.
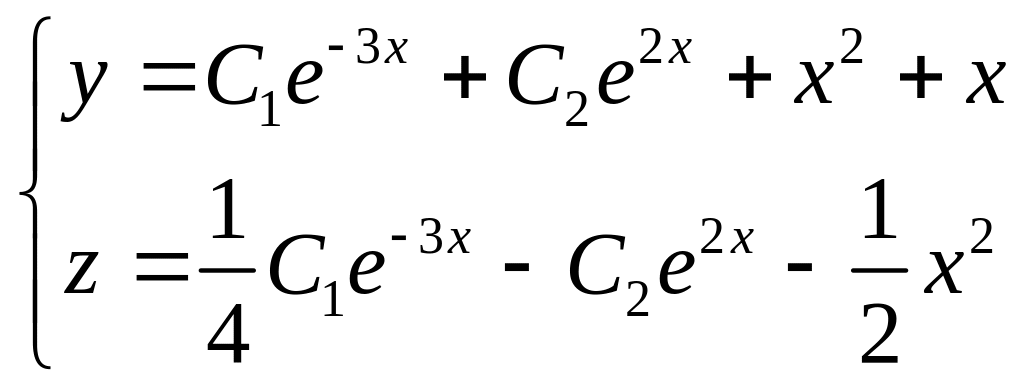Аналогично решаются системы с большим числом уравнений.
Задачи для самостоятельного решения
1.
2.
3.
4.
5.
6.
7.
Ответы:
1.
;
.
2.
;
.
3.
;
.
4.
.
.
5.
;
;
.
6.
;
.
7.
;
.