
- •Методические указания
- •Часть 4
- •Методические указания
- •Часть 4
- •Практические занятия
- •Задачи для самостоятельной работы
- •Решение. Разделим переменные ;
- •Интегрируем обе части, полученного равенства
- •Возвращаясь к переменной у , получаем
- •Задачи для самостоятельного решения
- •Разделяя переменные, получим
- •Задачи для самостоятельного решения
- •Занятие 4. Линейные уравнения первого порядка. Уравнения Бернулли.
- •Пример 1. Решить уравнение
- •Занятие 5. Уравнения, допускающие понижение порядка
- •Пример 1. Найти частное решение уравнения
- •Разделяя переменные, находим
- •Следовательно, . Окончательно получим
- •Рассмотрим линейное однородное уравнение второго порядка
- •Занятие 7. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида Пусть имеем уравнение
- •Правая часть данного неоднородного уравнения имеет вид
- •Правая часть данного неоднородного уравнения имеет вид
- •Библиографический список
- •Занятие 7. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида…………………………….30
- •Методические указания
- •Часть 4
- •Подписано к изданию 20.11.2013. Уч.- изд. Л. 2,6.
- •394026 Воронеж, Московский просп., 14
Занятие 4. Линейные уравнения первого порядка. Уравнения Бернулли.
Линейным называется уравнение вида
![]() (1)
(1)
где
![]() и
и
![]() -
заданные непрерывные функции или
постоянные.
-
заданные непрерывные функции или
постоянные.
Решение уравнения (1) будем искать методом Бернулли. Сделаем замену
у = u (x) v (x). (2)
Одну из функций u (x) или v (x) можно взять произвольной, другая определится на основании уравнения (1). Дифференцируя обе части равенства (2), находим
![]() .
.
Подставляя полученное выражение производной в уравнение (1), будем иметь
![]() или
или
![]() .
(3)
.
(3)
Выберем
функцию v такой, чтобы
выражение в скобках обратилось в нуль
![]() .
Разделяя переменные в полученном
уравнении относительно v,
находим
.
Разделяя переменные в полученном
уравнении относительно v,
находим
![]() .
Интегрируя, получим
.
Интегрируя, получим
![]() ,
или
,
или
![]() .
.
Так как достаточно какого-нибудь
отличного от нуля решения уравнения,
то за функцию v(x)
можно взять
![]() ,
где
,
где
![]() -
какая-нибудь первообразная. Очевидно,
что v (x)0.
Подставляя найденное значение v
(x) в уравнение (3),
получим
-
какая-нибудь первообразная. Очевидно,
что v (x)0.
Подставляя найденное значение v
(x) в уравнение (3),
получим
![]() или
или
![]() ,
откуда
,
откуда
![]() .
Подставляя u и
v в формулу (2),
окончательно получим
.
Подставляя u и
v в формулу (2),
окончательно получим
![]() .
.
Пример 1. Решить уравнение
Решение. Пусть y=uv, тогда .
Подставляя
выражение
![]() в
исходное уравнение, получим
в
исходное уравнение, получим
![]()
![]() (4)
(4)
Для
определения v получим
уравнение![]() ,
т.е.
,
т.е.
![]() ,
откуда
,
откуда
![]() или
или
![]() .
Подставляя выражение функции v
в уравнение (4) получаем для определения
u уравнение
.
Подставляя выражение функции v
в уравнение (4) получаем для определения
u уравнение
![]()
![]() ,
или
,
или
![]()
![]() ,
откуда
,
откуда
![]() .
Следовательно, общий интеграл заданного
уравнения будет иметь вид
.
Следовательно, общий интеграл заданного
уравнения будет иметь вид
![]() .
.
Пример 2. Найти частное решение
дифференциального уравнения
![]() ,
удовлетворяющее начальному условию
у(0) =1.
,
удовлетворяющее начальному условию
у(0) =1.
Решение. Положим y=uv, тогда .
![]() .
Определим v так,
чтобы выражение в скобках обратилось
в нуль. Тогда
.
Определим v так,
чтобы выражение в скобках обратилось
в нуль. Тогда
![]() .
Разделяя переменные, получим
.
Разделяя переменные, получим
![]() .
Интегрируя уравнение, найдем
.
Интегрируя уравнение, найдем
![]() или
или
![]()
Для определения u имеем уравнение
![]() ,
,
![]() ;
;
![]() .
.
Умножив u на
v, получим
общее решение
![]() .
.
Используя начальное условие у(0) =1, найдем 1= сos0 (sin0+C), откуда С=1. Искомое частное решение будет
![]() .
.
Метод Бернулли можно использовать и при интегрировании уравнения Бернулли, которое имеет вид
![]() ,
где
,
где
![]() .
.
Пример 3. Найти решение дифференциального
уравнения
![]() .
.
Решение. Это уравнение Бернулли. Положим y=uv, тогда
![]() ;
;
![]()
Определим v так,
чтобы выражение в скобках обратилось
в нуль. Тогда
![]() ,
разделяя переменные, получим
,
разделяя переменные, получим
![]() .
Интегрируя уравнение, найдем
.
Интегрируя уравнение, найдем
![]() или
или
![]() .
Для определения u
имеем уравнение
.
Для определения u
имеем уравнение
![]() ;
;
![]() ;
;
![]() ;
;
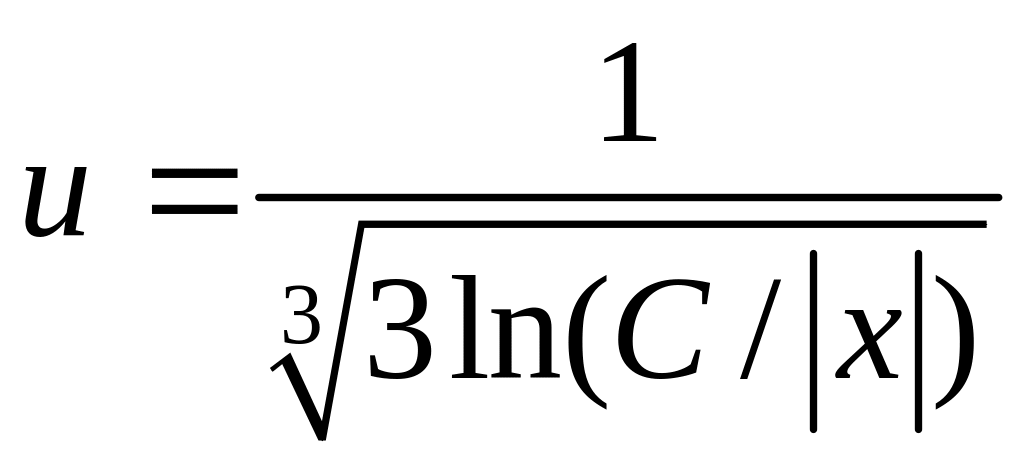 .
.
Окончательно получим
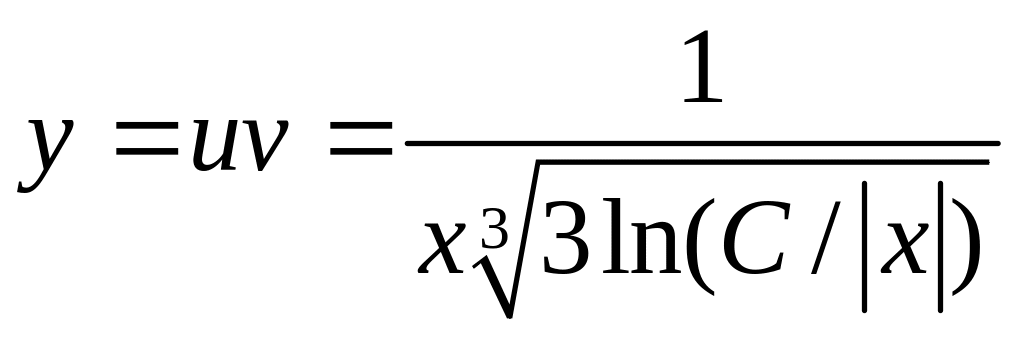 .
.
Задачи для самостоятельного решения
1.
![]() Ответ:
Ответ:
![]()
2.
![]() Ответ:
Ответ:
![]()
3.
![]() Ответ:
Ответ:
![]()
4.
![]() Ответ:
Ответ:
![]()
5.
![]() Ответ:
Ответ:
![]()
6.
![]() Ответ:
Ответ:
![]()
7.
![]() Ответ:
Ответ:
![]()
8.
![]() Ответ:
Ответ:
![]()
9.
![]() Ответ:
Ответ:
![]()
10.
![]() Ответ:
Ответ:
![]()
11.
![]() Ответ:
Ответ:
![]()
Занятие 5. Уравнения, допускающие понижение порядка
1.
Рассмотрим уравнение вида
![]() ,
которое не содержит явным образом
искомой функции у.
,
которое не содержит явным образом
искомой функции у.
Положим
![]() .
Тогда
.
Тогда![]() .Подставляя
эти выражения производных в исходное
уравнение получим уравнение первого
порядка
.Подставляя
эти выражения производных в исходное
уравнение получим уравнение первого
порядка
![]()
относительно
неизвестной функции р от х.
Проинтегрировав это уравнение, находим
его общее решение р = р (х, С1),
а затем из соотношения
получаем общий интеграл исходного
уравнения
![]() .
.
