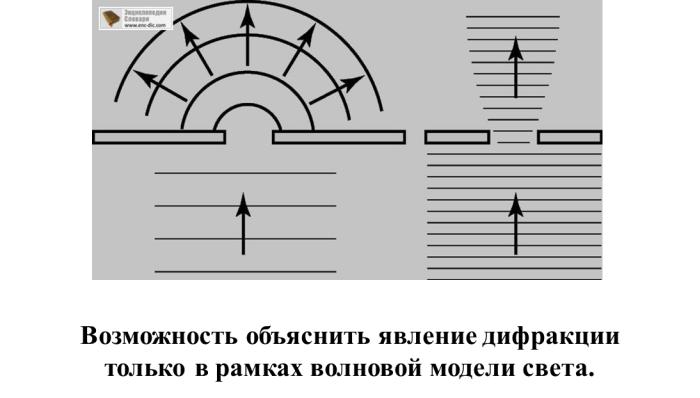
Явление дифракции
Свет с длиной волны сравнимой или большей чем ширина щели - распространение во всех возможных направлениях после прохождения через щель.
21
Зоны Френеля
Бесчисленное множество точек фронта волны, являющихся когерентными источниками новых волн,
– необходимость громоздкого интегрирования.
Метод зон Френеля – изящный метод разделения фронта волны на зоны,
таким образом что волны от соседних зон приходят в точку наблюдения в противоположной фазе
и ослабляют друг друга.
Использование принципа Гюйгенса и закона интерференции для анализа дифракционных явлений.
22
Приближения Фраунгофера и Френеля при описании дифракции
Дифракция Френеля или дифракция в ближней зоне:
•расстояния от источника света до объекта (отверстия, диска, щели) и от объекта до экрана сравнимы с размерами объекта, на котором происходит дифракция света,
•размер объекта составляет одну или несколько зон Френеля.
Дифракция Фраунгофера или дифракция в дальней зоне:
•расстояния от источника света до объекта и от объекта до экрана велики по сравнению с размерами объекта, на котором происходит дифракция света,
•плоский фронт как у падающей, так и у дифрагировавшей волн,
•размер объекта много меньше первой зоны Френеля.
23
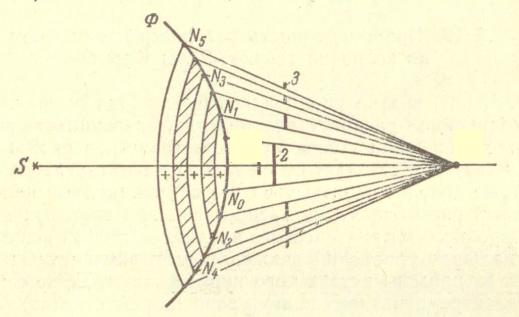
Зоны Френеля
О |
Р |
S – точечный источник монохроматического света в однородной среде, Ф – положение фронта волны в некоторый момент времени,
P – произвольная точка волны перед фронтом.
24
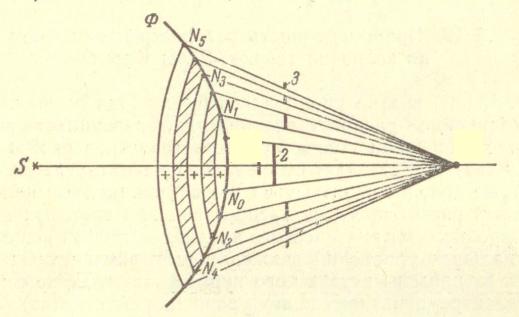
Зоны Френеля
О |
Р |
Приход в точку Р волн от всех точек фронта.
Деление фронта на ряд кольцевых зон с центрами в точке М и радиусами РN1 = РО + /2,
РN2 = РО1+ /2 = РО + 2 /2, РN3 = РО2+ /2 = PО + 3 /2,
………………………….. 25
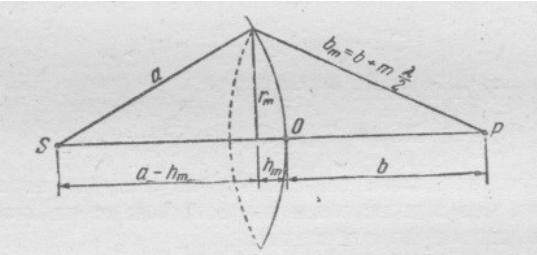
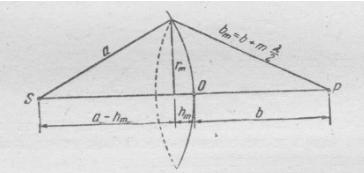
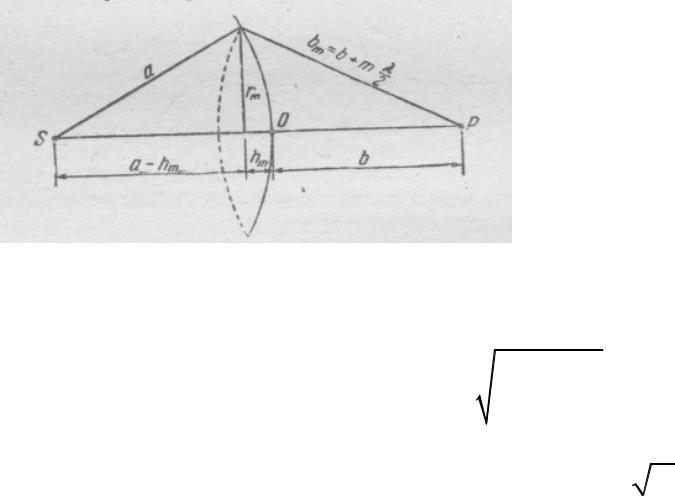
Зоны Френеля
a – радиус волновой
поверхности,
rm – радиус внешней границы m-й зоны.
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
bm m |
2 |
2 |
||||
|
2 |
|
2 |
|
|
m |
2 |
|
|
|
|
m |
2 |
hm |
|
|
||||||||
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||
r |
|
a |
|
|
|
a h |
|
b m |
2 |
|
|
b h |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
a b |
|
||||
2 |
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
bm |
||
rm |
2ahm hm bm m |
|
|
|
|
2bhm hm |
|
|
мало: |
hm |
|
|
|
|
||||||||||
|
|
|
2 a b |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
h |
|
bm |
|
2 |
a b |
||
m |
|||
|
|
Зоны Френеля
Площадь сферического сегмента S 2 Rh
Площадь m зон Френеля S |
|
2 ah |
|
ab |
m |
m |
|
||||
|
m |
|
a b |
||
|
|
|
|
||
Площадь m-й зоны Френеля Sm Sm |
Sm 1 ab |
||||
|
|
|
|
|
a b |
Вывод: |
|
|
|
|
|
при не слишком больших m площади зон Френеля примерно одинаковы.
27
Зоны Френеля
Показано ранее:
r2 |
2ah |
h2 |
||
m |
|
|
m |
m |
h |
|
2 |
bm |
|
m |
|
|
|
|
Небольшие m (высота сегмента hm << a):
r2 |
2ah |
rm |
ab |
m |
|
||||
m |
m |
|
a b |
|
|
|
|
||
Вывод: радиус зон пропорционален m.
28
Зоны Френеля
С учетом различия в расстояниях до Р и углов, под которыми видны площади зон из Р,
А1 > А2 > А3 > … > Аm-1 > Аm > Аm+1 > …
Полная амплитуда волны, приходящей в Р,
А = А1 - А2 + А3 - А4 + …
Допустимое приближение при монотонном убывании Am
|
|
|
|
|
|
А |
Аm 1 Am 1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
m |
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А |
А1 |
|
|
А1 |
А |
А3 |
|
|
|
|
А3 |
А |
А3 |
|
... |
А1 |
||
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
2 |
2 |
2 |
|
|
|
2 |
2 |
2 |
|||||||
|
|
|
|
|
|
2 |
|
|
|
|||||||||
Полная амплитуда волны, приходящей в Р, равна половине амплитуды волны, создаваемой 1-й зоной Френеля.
29
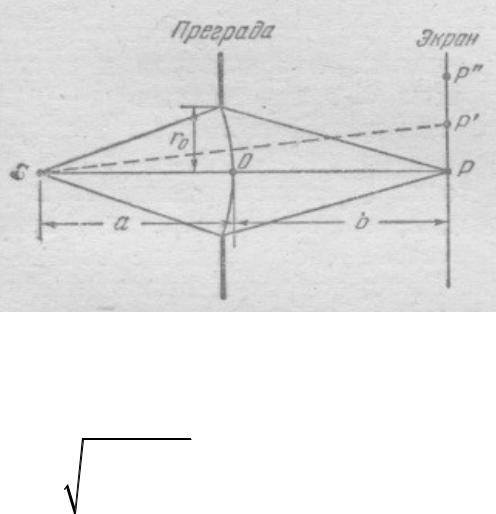
Дифракция Френеля от круглого отверстия
Радиус отверстия r0 a,b :
a – расстояние от источника до преграды, b – расстояние от преграды до точки P.
r0 |
ab |
m - открыто m зон Френеля |
|
a b |
|||
|
|
30