Содержание предыдущей лекции
Атомная физика
Квантовая модель атома водорода. Волновые функции атома водорода. Физический смысл квантовых чисел.
1
Контрольный вопрос
Число возможных подоболочек для оболочки с n = 4 в атоме водорода равно
(a) 5 |
(б) 4 |
(в) 2 |
(г) 1. |
Число подоболочек равно числу разрешенных значений l. Разрешенными значениями l для n = 4 являются l = 0, 1, 2, 3. В результате ответ – 4 подоболочки.
(б)
2
Cодержание сегодняшней лекции
Aтомная физика
Принцип исключительности. Многоэлектронные атомы.
Принцип исключительности и периодическая таблица. Электронные конфигурации химических элементов. Оптические и рентгеновские атомные спектры. Спонтанные переходы.
Вынужденные переходы. Лазеры.
3
Принцип исключительности и периодическая таблица
4
Принцип исключительности
Возможность предсказания и описания числа состояний, доступных для атомов, с помощью четырех квантовых чисел n, l, ml и ms.
Связь четырех квантовых чисел со всеми возможными электронными состояниями атома с большим количеством электронов.
Австрийский физик Вольфгангом Паули (1900-1958) – открытие принципа исключительности (1925 г.):
электроны в атоме всегда находятся в различных квантовых состояниях.
Следствие: набор квантовых чисел для любых двух электронов в одном и том же атоме не может быть одинаковым.
5
Принцип исключительности
Последствия невыполнения принципа исключительности:
излучение атомом энергии до тех пор, пока каждый из электронов в атоме не оказался бы на самом низшем из возможных энергетическом уровне.
Прогнозируемый результат - сильное видоизменение химических свойств элементов,
невозможность существования Природы в том виде, какой характерен для нее в настоящее время.
6
Многоэлектронные атомы
Электронная структура сложных атомов – последовательность заполненных оболочек, расположенных в порядке нарастания энергии.
Оболочки - различные главные квантовые числа n.
Подоболочки - одинаковое главное квантовое число n, но различные орбитальные квантовые числа l.
Порядок заполнения оболочек в атоме:
по мере заполнения оболочки попадание следующего электрона на располагающуюся выше вакантную оболочку
с минимальной из возможных энергией.
7
Многоэлектронные атомы
Атомная орбиталь – одинаковые значения квантовых чисел n, l, разные значения квантового числа ml.
Следствие принципа исключительности:
нахождение на любой из орбиталей только двух электронов с ms = + 1/2 и ms = - 1/2.
Ограниченное число электронов в различных оболочках (K, L, M, …) с разными n.
8
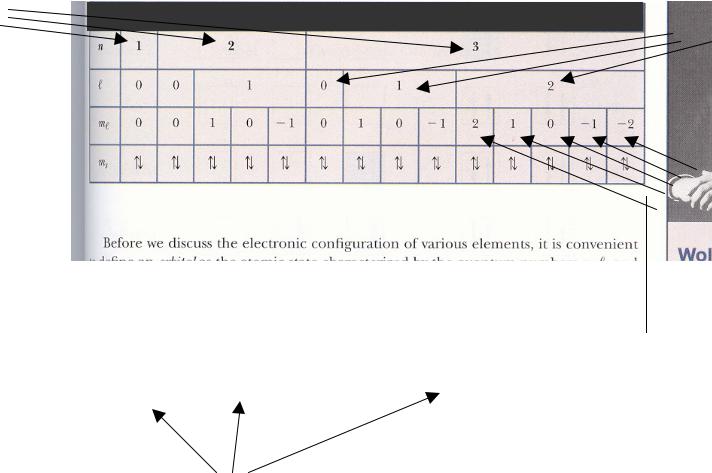
Принцип исключительности и периодическая таблица
Оболочка |
Разрешенные квантовые состояния со значением n вплоть до 3 |
Подоболочки |
{ { { { { { { { { { { { { { |
|||||||||||||||
|
2 |
|
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|
|
|
{ |
|
|
|
{ |
|
|||||||
|
|
|
|
|
|
|
{ |
|
|
|
|
|
|||
|
2 |
|
|
2+6=8 |
|
|
|
2+6+10=18 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 12 |
|
2 22 |
|
|
|
|
|
2 32 |
|
|
|
||||
Oрбитали
до 2n2 электронов на каждой оболочке
9
Принцип исключительности и периодическая таблица
Равенство атомного числа Z числу протонов в ядре атома химического элемента.
Z электронов в нейтральном атоме этого элемента.
Водород H Z = 1
Основное состояние - два возможных набора квантовых чисел:
n = 1, l = 0, ml = 0, ms = +1/2
и
n = 1, l = 0, ml = 0, ms = -1/2.
Электронная конфигурация
1s1.
1s – |
Присутствие |
|
состояние, в |
||
1 электрона в |
||
котором |
||
s оболочке |
||
n = 1, l = 0 |
||
|
Гелий He Z = 2
Два электрона в основном состоянии с квантовыми числами
n = 1, l = 0, ml = 0, ms = +1/2
и
n = 1, l = 0, ml = 0, ms = -1/2.
Невозможность других комбинаций этих квантовых чисел (оболочка K заполнена).
Электронная конфигурация - 1s2.
10