Содержание предыдущей лекции

Aтомная физика

Ранние модели атома

Модель Томсона. Модель Резерфорда.

Эксперимент Франка-Герца. Боровская модель атома водорода. Боровский принцип соответствия.

1

Контрольный вопрос

Общая энергия атома водорода:

а) положительна, б) отрицательна, в) равна нулю?

Общая энергия атома E kee2

2r

б)

2

Содержание сегодняшней лекции

Атомная физика

Квантовая модель атома водорода. Волновые функции атома водорода. Физический смысл квантовых чисел.

3

Квантовая модель атома водорода

4

Боровская модель атома водорода

Затруднения теории Бора:

1)Прецизионные спектроскопические измерения: многие линии в серии Бальмера и других сериях вовсе не являются одиночными (синглетами), каждая из линий представляет собой группу линий, очень тесно расположенных рядом друг с другом.

2)Расщепление в некоторых случаях при помещении атомов в сильное магнитное поле определенных одиночных спектральных линий на три близко расположенные линии.

5

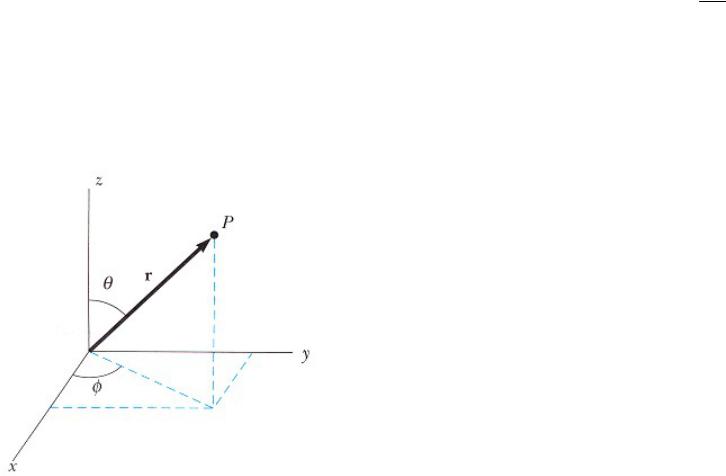
Квантовая модель атома водорода

Полностью квантовая модель, базирующаяся на уравнении Шредингера, - преодоление затруднений теории Бора.

Функция потенциальной энергии для атома водорода U r ke er2 .

3D случай: нахождение волновых функций как решений уравнения

Замена прямоугольной системы отсчета на сферическую для учета симметрии атома и упрощения рассмотрения вопроса.

6

Квантовая модель атома водорода

Волновая функция r, , R r f g .

Необходимость решить три уравнения для R(r), f( ) и g( ).

Требование: удовлетворение граничных условий для каждого из решений этих уравнений.

Пример: конечные значения R(r) при r = 0 и r = , g( ) = g( + 2 ).

7

Квантовая модель атома водорода

Три различных квантовых числа, характеризующих каждое из разрешенных состояний атома водорода, -

результат применения граничных условий ко всем трем волновым функциям.

Квантовые числа – только целые и соответствуют трем независимым степеням свободы

(трехмерное пространство).

8

Квантовая модель атома водорода

Главное квантовое число n - ассоциация с радиальной функцией R(r).

Радиальная функция - отражение вероятности обнаружения электрона на определенном радиальном расстоянии от ядра.

Зависимость функции потенциальной энергии системы «электрон-ядро» только от радиальной координаты r и ни от одной из угловых координат

Полное согласие этого уравнения с теорией Бора.

9

Квантовая модель атома водорода

Ассоциация орбитального квантового числа l и орбитального магнитного квантового числа ml с орбитальным моментом импульса электрона L.

Получение важных соотношений между тремя квантовыми числами, а также определенных ограничений,

накладываемых на целочисленные значения полной волновой функции, в результате применения граничных условий ко всем трем ее частям:

n может изменяться от 1 до , l может изменяться от 0 до n – 1, ml может изменяться от - l до l.

10