Квантовая модель атома водорода
Три квантовых числа для атома водорода |
|
|||
Квантовое |
Название |
Разрешенные значения |
Число разрешенных |
|
число |
|
состояний |
||
|
Главное квантовое |
Любое значение |
||
|
|
число |
|
|
Орбитальное квантовое число
Орбитальное
магнитное квантовое число
11
Квантовая модель атома водорода
Формирование электронной оболочки всеми состояниями, имеющими одинаковые главные квантовые числа n.
Формирование подоболочки всеми состояниями, имеющими одинаковые значения n и l.
Обозначения электронных оболочек и подоболочек
Символ |
Символ |
Состояние 3p – |
оболочки |
подоболочки |
квантовые числа n = 3 и l = 1. |
|
|
Состояние 2s – квантовые числа n = 2 и l = 0.
12
Квантовая модель атома водорода
|
|
|
|
Обозначения электронных оболочек |
||
|
Три квантовых числа для атома водорода |
и подоболочек |
|
|||
|
Символ |
Символ |
||||
Квантовое |
Название |
Разрешенные |
Число разрешен- |
|||
оболочки |
подоболочки |
|||||
число |
|
значения |
ных состояний |
|
|
|
|
Главное квантовое |
|
Любое значение |
|
|
|
|
число |
|
|
|
|
|
Орбитальное квантовое число
Орбитальное магнитное квантовое число
Запрет на существование состояний, в которых могли бы нарушиться правила для квантовых чисел.
Пример: состояние 2d с n = 2 и l = 2 не может существовать, потому что самое большое разрешенное значение l равно n -1, а в данном случае оно равно 1.
n = 2: состояния 2s и 2p разрешены, а состояния 2d, 2f, … не разрешены. n = 3: разрешены подоболочки 3s, 3p и 3d.
13
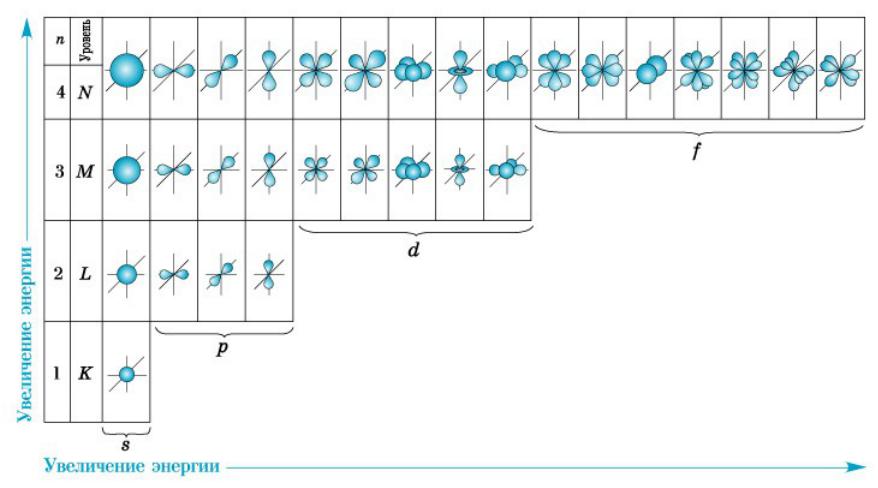
Форма и размер электронных орбиталей атомов элементов
14
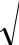
Волновые функции атома водорода
Самая простая волновая функция состояния 1s атома водорода
|
1s r |
|
1 |
|
e r / a0 , где a0 – радиус Бора. |
|
|
|
|
||
|
a3 |
||||
|
|
|
|
|
|
|
|
|
0 |
|
|
1s |
нормирована, стремится к нулю по мере стремления r к . |
||||
Сферическая симметрия 1s, зависимость только от r.
Характерная сферическая симметрия всех s состояний.
15
1s r |
|
1 |
|
e |
r / a0 |
|
|
|
|
||
a03 |
|
Волновые функции атома водорода
|
|
|
|
2 |
|
1 |
|
|
2r / a0 |
|
|
|
|
|
|
||||||
Состояние 1s: плотность вероятности |
|
|
|
|
|
|
e |
. |
||
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||
|
|
1s |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
а0 |
|
|
|
|
2 dV - вероятность обнаружения электрона в элементе объема dV.
Функция плотности радиального распределения P(r) –
радиальная линейная плотность вероятности обнаружения электрона в сферической оболочке радиуса r и толщиной dr.
P(r)dr – вероятность обнаружения электрона в этой |
|
оболочке. |
16 |
Волновые функции атома водорода
|
dV 4 r 2dr |
|
|
P r dr |
|
|
|
2 dV |
|
|
|
2 4 r 2dr |
|||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
Функция плотности радиального распределения |
P r 4 r 2 |
|
|
|
2 . |
||||||||||||||||||||
|
|
||||||||||||||||||||||||
2 |
|
1 |
|
|
2r / a0 |
|
|
|
|
|
|
4r |
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2r / a0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1s |
|
|
|
|
e |
|
|
P r |
|
|
|
|
|
|
e |
|
|
|
|
|
||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
а0 |
|
|
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
|
|||||
|
|
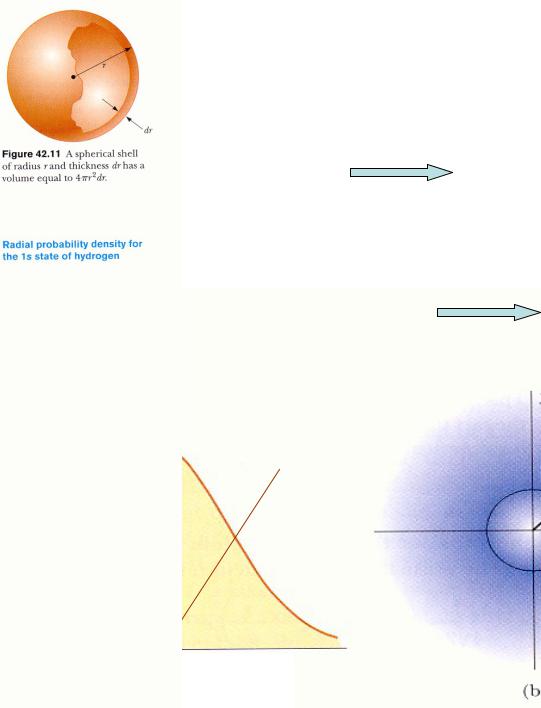
наиболее вероятное значение r |
|
|
|
|
Асимметрия функции |
||||||||||||||||||
|
|
радиального распределения. |
|||||||||||||||||||||||
|
|
|
для конкретного состояния |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Квантовая механика: |
||||||||||||||||
|
|
|
|
|
|
|
|
отсутствие резко очерченной границы |
|||||||||||||||||
|
|
|
|
|
|
|
|
у атома (в отличие от теории Бора). |
|||||||||||||||||
|
|
|
|
|
|
|
Распределение вероятности обнаружения электрона |
||||||||||||||||||
|
|
|
|
|
|
|
|
– распределение заряда электрона |
|||||||||||||||||
|
|
|
|
|
|
|
в области пространства (электронном облаке). |
||||||||||||||||||
α0 = 0,0529 нм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|||||||
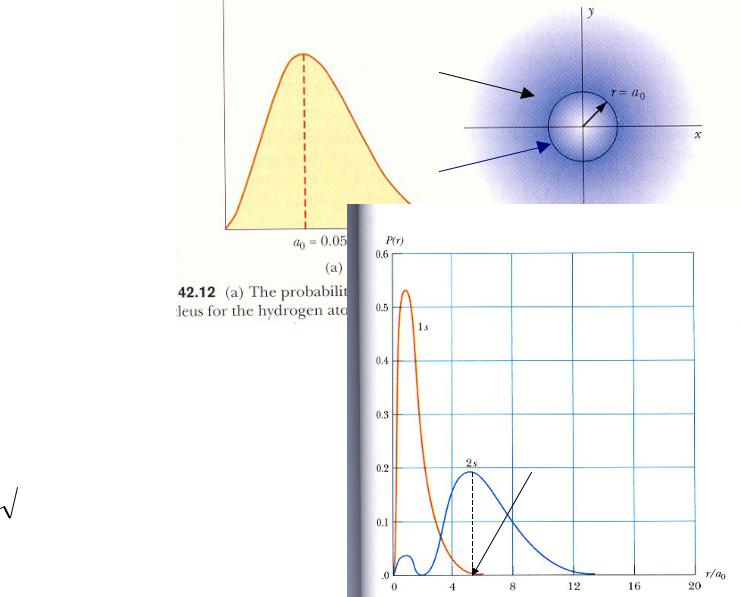
Волновые функции атома водорода
Распределение плотности вероятности обнаружения электрона в атоме водорода в состоянии 1s (плоскость xy).
Наиболее вероятное расстояние r
между электроном и центром атома
Состояние 2s (n = 2, l = 0):
сферическая симметрия нормированной волновой функции.
2s r |
1 |
|
|
1 |
|
3/ 2 |
|
|
r |
|
r2 5 a0 |
|
|
|
|
r / 2a0 |
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
4 2 |
|
|
|
|
|
|
|
e |
|
|||
|
|
a0 |
|
|
|
|
a0 |
|
||||
18
Физический смысл квантовых чисел
Орбитальное квантовое число l
Классическая физика:
произвольное значение орбитального момента импульса электрона L.
Боровская модель атома:
квантованные значения орбитального момента импульса электрона L = nħ.
Затруднения:
некорректное предсказание L=ħ для атома водорода в основном состоянии.
Квантово-механическая модель атома:
отказ от представлений о движении электрона по орбите.
Возможность у атома в состоянии с основным квантовым числом n
иметь только дискретные значения орбитального момента импульса:
L |
|
|
|
|
|
l 0, 1, |
2, ...,n 1 |
|
|
l |
l |
|
1 |
|
|||
19
Физический смысл квантовых чисел
Орбитальное магнитное квантовое число ml
Классическая физика:
создание кругового электрического тока электроном, движущимся по орбите.
Магнитный момент кругового тока IA,
I – ток,A направление перпендикулярно круговому току,
соответствие величины площади, охватываемой током.
20