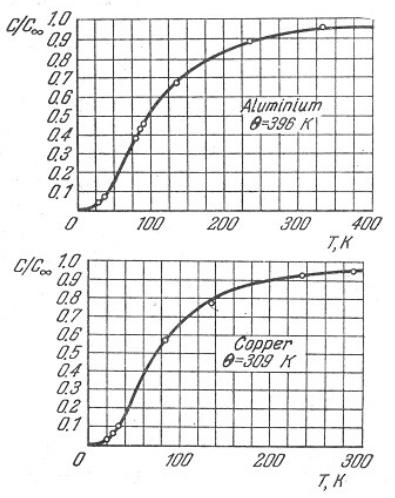
Теплоемкость кристаллов
Теория Дебая
C - классическое значение, полученное из уравнения квантовой механики для T .
○ - экспериментальные данные
Сплошные кривые – результат теоретических расчетов в рамках теории Дебая
12
Теплоемкость кристаллов
Фононы
Сопоставление энергии каждого нормального колебания с частотой i
энергии квазичастицы, называемой фононом,
i i .
Возможность представления внутренней энергии кристалла в виде суммы энергии нулевых колебаний и энергии фононов
3Nr |
1 |
|
U ni |
2 |
i |
i 1 |
|
N – число элементарных ячеек в кристалле, r – число атомов в ячейке, ni – число фононов (нормальных колебаний) с частотой i.
13
Теплоемкость кристаллов
Фононы
Протекание многих процессов в кристалле, например, рассеяния рентгеновских лучей или нейтронов кристаллом,
таким образом, как если бы фонон обладал квазиимпульсом
p k ,
k - волновой вектор, соответствующий нормальному колебанию.
14
Теплоемкость кристаллов
Фононы
Отличие фонона от обыкновенных частиц (электронов, протонов, фотонов и т.д.) – невозможность существования фонона в вакууме – необходимость среды для образования и существования фонона.
Частицы, существующие только в какой-либо среде, - квазичастицы.
15
3Nr |
1 |
|
|
|
1 |
|
|
|
U ni |
|
i |
i i |
|
|
|
|
|
2 |
2 |
exp / kT 1 |
||||||
i 1 |
|
|
|
|
Теплоемкость кристаллов
Фононы
Возможность описания колебаний атомов с помощью фононного газа, заключенного внутри кристалла.
Среднее число фононов с частотой i в кристалле
(как следует из сопоставления уравнений для внутренней энергии и средней энергии колебаний с частотой )
ni 
exp i1/ kT 1.
Следствие: возможность одновременного существования неограниченного числа одинаковых фононов (в одном и том же состоянии) в кристалле.
Заключение: принцип исключительности не распространяется на фононы.
16
Теплоемкость кристаллов
Фононы
Сходство между фононным газом и фотонным газом, представляющим э-м излучение в полости.
Существенная разница: фотоны - истинные частицы, фононы - квазичастицы.
17
Теплоемкость кристаллов
Фононы
Распределение |
ni |
|
1 |
|
exp i / kT 1 |
||||
|
|
|
- частный случай распределения Бозе-Эйнштейна, которому подчиняются частицы, имеющие целый (в частности, нулевой) спин.
Вид общего выражения для этого распределения ni |
|
|
1 |
|
|
, |
|
exp |
E |
|
/ kT 1 |
||||
где ni |
|
|
|
i |
|
||
- среднее число частиц в состоянии с номером i, |
|
|
|
|
|||
Ei |
- энергия частицы в этом состоянии, |
|
|
|
|
|
|
|
- так называемый химический |
ni N . |
|
|
|
||
|
потенциал, определяемый из условия |
|
|
|
|||
18
Теплоемкость кристаллов
|
|
|
|
|
|
|
Фононы |
||
Распределение ni |
|
|
|
|
1 |
|
|
|
- основа статистики Бозе-Эйнштейна. |
|
|
|
|
|
|
|
|||
|
|
i |
|
|
|
||||
|
|
exp |
|
E |
|
/ kT 1 |
|
||
Бозоны - частицы, подчиняющиеся статистике Бозе-Эйнштейна.
Фотоны и фононы - бозоны.
Все частицы с нулевым или целым спином - бозоны.
Вероятность P появления (“рождения”) бозона в состоянии,
где уже находится n частиц, пропорциональна корню квадратному из n:
P n.
Бозоны – коллективисты,
им “нравится” собираться в oдном и том же состоянии.
19
Электропроводность
20
Теория свободных электронов в металлах
Классическая теория электропроводности металлов:
движение в металле через решетку с фиксированными в ее узлах ионами классического газа электронов проводимости.
Качественное предсказание зависимости, описываемой законом Ома.
Проблема:
некорректное предсказание численных значений электро- и теплопроводностей.
21