25. Вполне смешанная игра. Решение матричной игры n´n методом обратной матрицы.

26. Сведение матричной игры n´m к двойственной задаче линейного программирования. Общий подход. Методика решения матричной игры n´m симплекс-методом.

https://vk.com/doc132303406_572185909?hash=aca3d74fd593001f6b&dl=4fcf6cfa13cd529d0d

Сформулируем кратко алгоритм симплекс-метода с использованием симплекс-таблиц.

Симплекс-метод основан на утверждении о том, что линейная функция F(x) (или G(y) ) задачи линейного программирования достигает своего оптимума (максимума или минимума) в одной из угловых точек многогранника решений, который определяется неравенствами (29) или (33). Идея симплекс-метода состоит в направленном переборе угловых точек с последующим уменьшением значений целевой функции F(x) для задачи на минимум (или у

27. Неантагонистические игры. Биматричные игры. Постановка задачи. Функции выигрышей.

Биматричной игрой называется конечная бескоалиционная игра двух лиц. Пусть игрок A имеет m стратегий, а игрок B – n стратегий. Тогда биматричную игру можно описать двумя матрицами выигрышей A и B для игроков A и B :

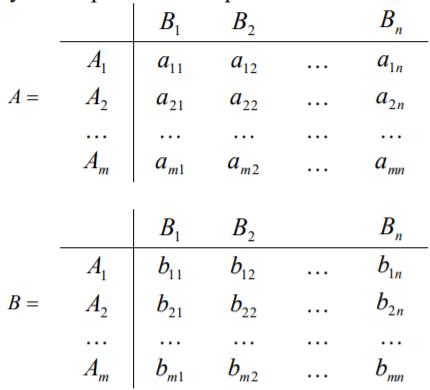
28. Примеры биматричных игр: дилемма узников, семейный спор, перекресток, ястребы-голуби и др.

Примеры решения: https://vk.com/doc132303406_576428789?hash=8946299294db25597c&dl=677a9d8eaa89bfb0c2

Пример 2. «Дилемма узников». Игроками являются два узника, находящихся в камере предварительного заключения по подозрению в совершении преступления. При отсутствии прямых улик возможность их осуждения в большей степени зависит от того, заговорят они или будут молчать. Если оба будут молчать, то наказание им обоим составит ровно 1 год. Если оба сознаются, то получат срок 6 лет (признание учитывается как смягчающее обстоятельство). Если заговорит только один, а другой будет молчать, то заговоривший будет выпущен на свободу, а промолчавший получит максимально возможное наказание 9 лет.

Другие примеры

29. Принципы доминирования в биматричных играх. Пример для матриц размера 3´3. Наилучшие стратегии игроков.

30. Ситуация равновесия по Нэшу в биматричной игре произвольной размерности. Свойства ситуаций равновесия. Теорема Дж. Нэша.

31. Ситуация равновесия по Нэшу в биматричной игре 2´2. Поиск смешанных стратегий для двух игроков.

32. Графическая интерпретация решения в биматричной игре 2´2 по Нэшу. Сильно равновесные стратегии.

33. Оптимальность по Парето. Поиск оптимальных стратегий по Парето в биматричной игре 2´2. Множество Парето. Точка утопии.

34. Пример поиска оптимальных стратегий по Парето в играх «дилемма узников» и «семейный спор».

35. Принятие решений в условиях неопределенности. Статистические методы принятия решений. Виды неопределенностей.

Теория статистических решений отличается от теории игр тем, что неопределенная ситуация не имеет конфликтной окраски – никто никому не противодействует, но неопределённость присутствует. Неизвестные условия зависят не от сознательного действующего противника, а от обыкновенной действительности, которую в теории статистических решений принято называть природой, поведение которой неизвестно.

Риском игрока A при использовании им стратегии в условиях называется разность между выигрышем, который он получил бы, если бы знал , и выигрышем, который он получил в тех же условиях, применяя стратегию

Выделяют три степени неопределенности состояний природы:

1) вероятности состояний природа известны заранее (случай стохастической неопределенности)

2) вероятности неизвестны, но можно сделать предположения относительно их значений

3) вероятности неизвестны, и невозможно сделать оценку (даже приблизительно) их значений (случай полной неопределенности)