11. Аналитический метод решения задачи линейного программирования m X n (симплекс-метод). Для задач на максимум и минимум.

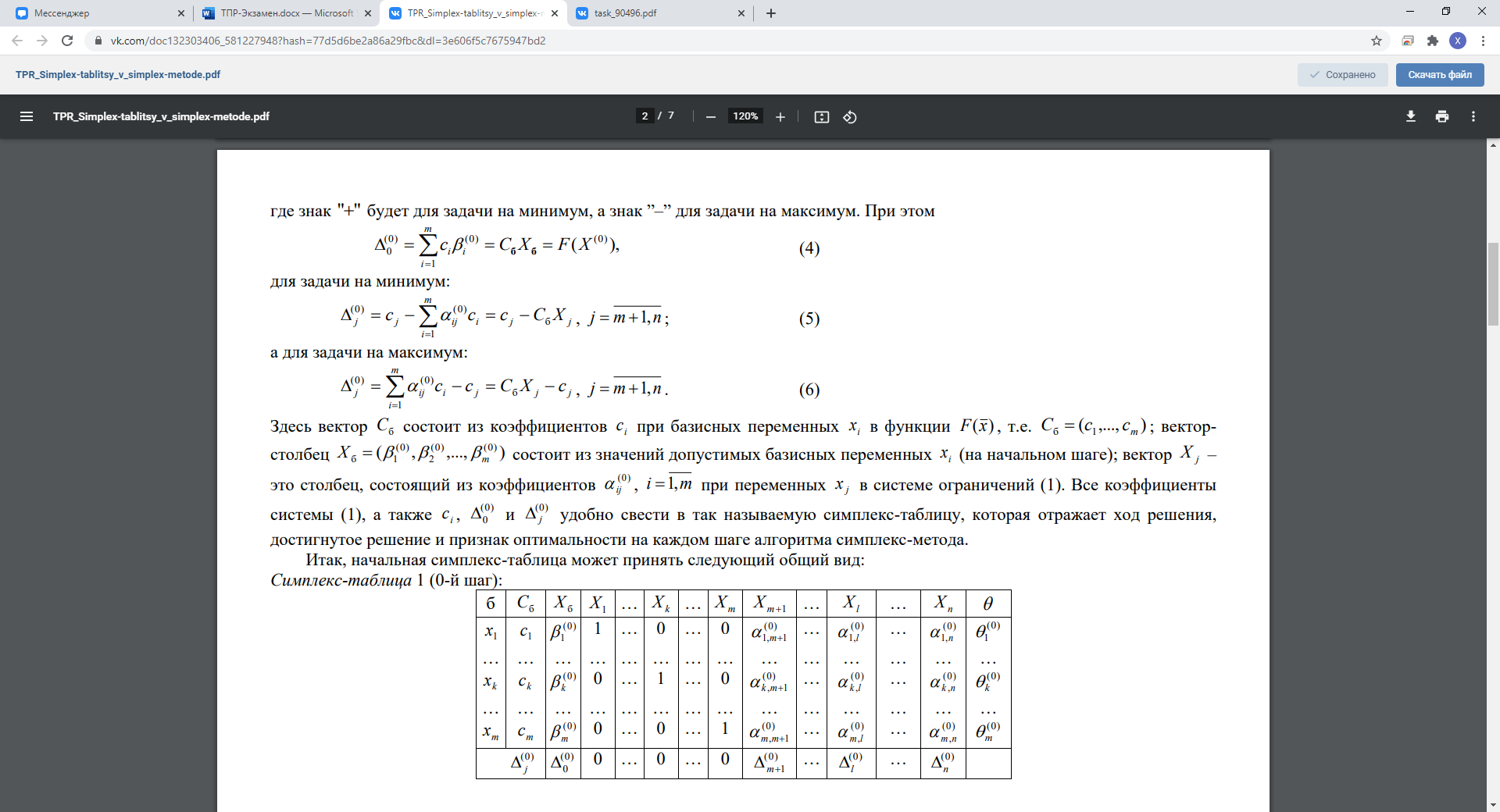
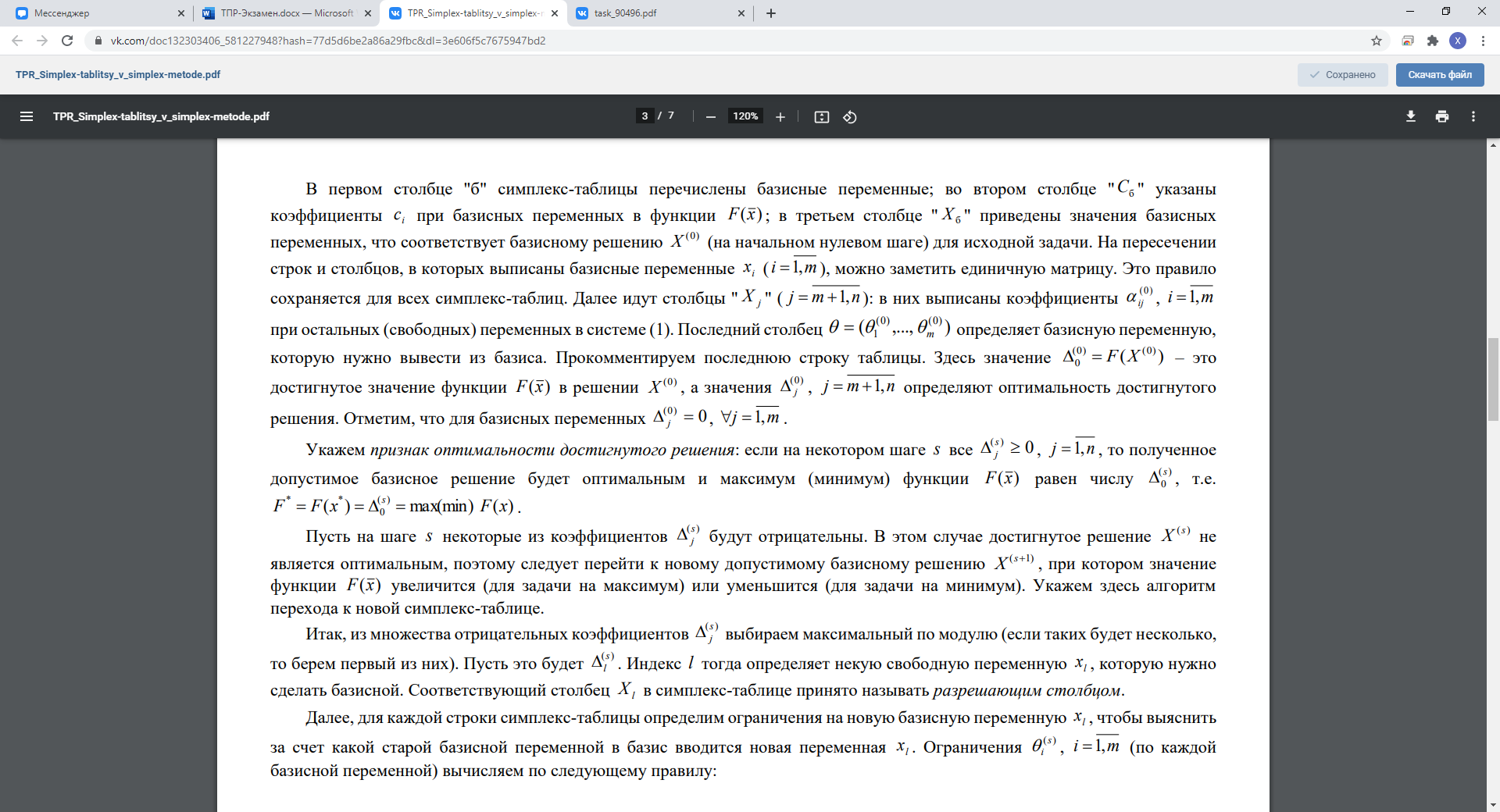
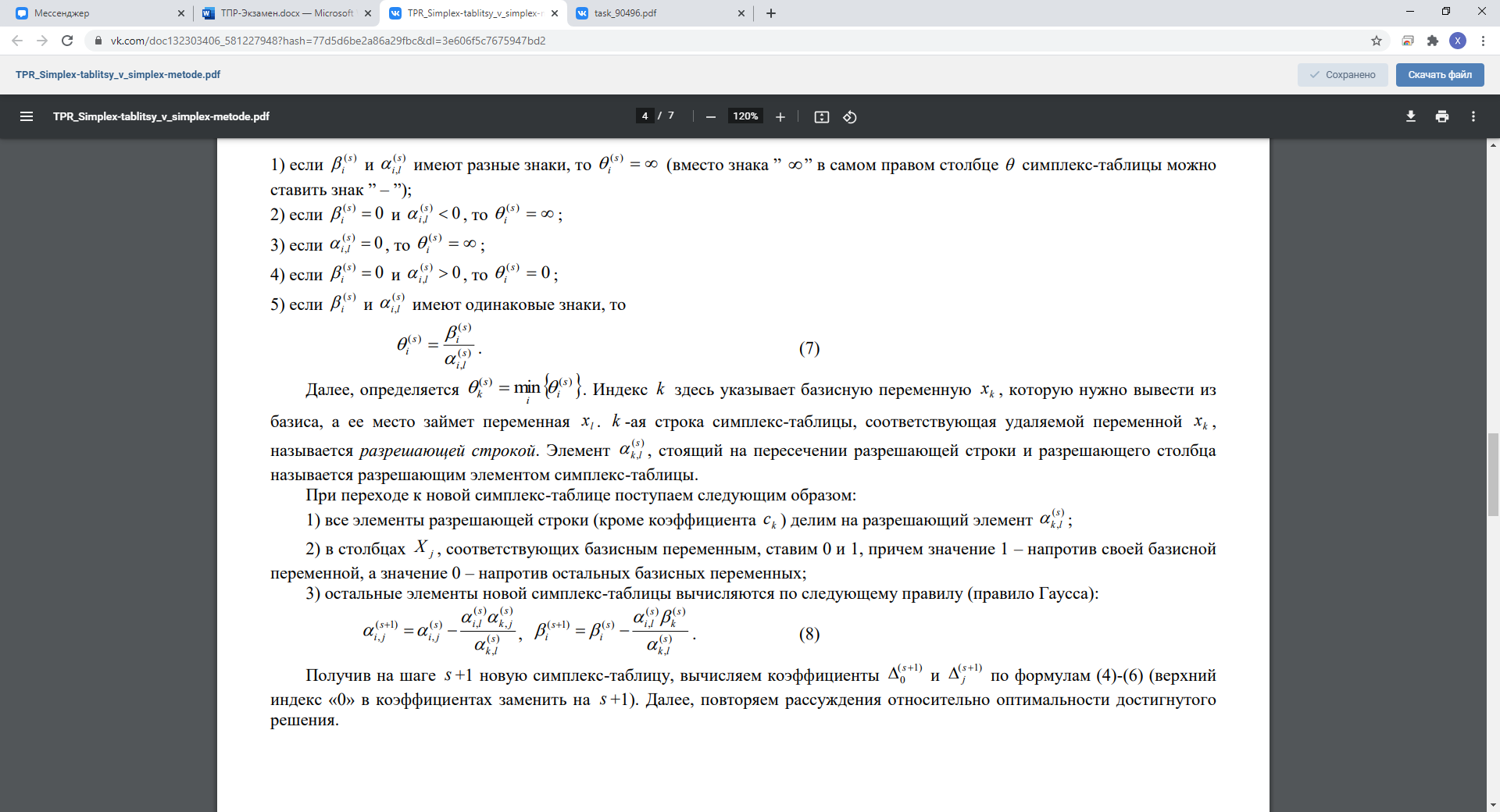
Практическая реализация симплекс-метода обычно сводится к последовательному построению так называемых симплекс-таблиц, в которых отражается очередная каноническая форма представления исходной задачи, а также содержится проверка условия оптимальности соответствующего опорного плана. В многочисленных учебных пособиях по линейному программированию представлены весьма различные варианты оформления этих таблиц. Ниже дается один из таких вариантов.

В первой строке табл. 2.1 обозначены названия столбцов. В следующих m строках отображаются коэффициенты перед переменными в ограничениях-равенствах задачи, а также свободные члены. В последней строке содержатся коэффициенты целевой функции, если решается задача на минимум, и коэффициенты целевой функции, взятые с противоположными знаками, если решается задача на максимум. В первом столбце перечисляются базисные переменные в соответствии с присутствием их в том или ином равенстве. Если симплекс-таблица составлена правильно, то в ней имеется m единичных столбцов (один элемент - единица, остальные элементы - нули), а свободные члены в ней неотрицательны.

Составим симплекс-таблицу примера:

По сравнению с табл. 2.1 в табл. 2.2. добавлен еще столбец для симплекс-отношений. В последней строке записаны коэффициенты целевой функции, взятые с противоположными знаками, так как L → max.

Данной симплекс-таблице, согласно выше приведенному правилу, соответствует опорный план (вершина) вида

x (0) = (0 0 0 12 18).

Условие оптимальности состоит в следующем: если в последней строке симплекс-таблицы все элементы неотрицательны, то соответствующий опорный план является оптимальным, и задача решена. В нашем случае условие оптимальности не выполняется, так как в последней строке имеется три отрицательных элемента. Поэтому необходимо перейти к новому опорному плану и соответственно построить новую симплекс-таблицу

Алгоритм симплекс-метода применим к примеру выше:

1. В последней строке исходной симплекс-таблицы выбираем наименьший отрицательный элемент. Он отмечен знаком *. Столбец, соответствующий этому элементу, называется ведущим. Он определяет переменную, которая будет введена в базис на данном этапе. Это - переменная х3.

2. Вычисляют отношения свободных членов к элементам ведущего столбца (симплекс-отношение): θ1=12/2=6, θ1=18/2=9. Находят наименьшее неотрицательное из этих симплекс-отношений. Оно соответствует ведущей строке, которая определяет переменную, выводимую из базиса. Это - переменная х4.

3. Если все симплекс-отношения окажутся отрицательными, то задача не имеет решений (оптимум целевой функции не достигается).

4. На пересечении ведущей строки и ведущего столбца находится ведущий элемент.

5. Если имеется несколько одинаковых по величине симплекс-отношений, то выбирают любое из них. То же самое относится к отрицательным элементам последней строки симплекс-таблицы.

6. После нахождения ведущего элемента переходят к следующей таблице (табл. 2.3). Для этого вначале заполняем первый столбец, записывая новые базисные элементы: х3 и х5.

7. Далее элементы ведущей строки табл. 2.2, за исключением симплекс-отношения, делим на ведущий элемент.

8. Остальные элементы ведущего столбца делаем равными нулю.

9. Оставшиеся элементы симплекс-таблицы вычисляются по правилу прямоугольника: мысленно вычерчиваем прямоугольник в табл. 2.2, одна вершина которого совпадает с разрешающим элементом, а другая - с элементом, образ которого мы ищем; остальные две вершины определяются 34 однозначно. Тогда искомый элемент из табл. 2.3 будет равен соответствующему элементу табл. 2.2 минус дробь, в знаменателе которой стоит разрешающий элемент, а в числителе - произведение элементов из двух неиспользованных вершин прямоугольника.

Например, элемент, стоящий на пересечении строки х3 и столбца x1 находим так: 7-2⋅2/2=5; свободный член в строке х5: 18-2⋅12/2=6; первый элемент последней строки: -3-2⋅(-6)/2=3 и т.д.

10. Записываем соответствующий опорный план:

x (1) = (0 0 6 0 6)

и снова проверяем условие оптимальности. На этот раз условие выполнено: в последней строке все элементы неотрицательны. Значит найденный опорный план оптимален. Чтобы получить оптимальный план исходной, стандартной задачи, нужно отбросить последние два элемента из x (1) : x* = (0 0 6).

11. Вычисляем оптимальное значение целевой функции: L*=3⋅0+4⋅0+6⋅6=36.

Пример в след вопросе!

12. Симплекс-таблицы в симплекс-методе для задач на максимум и минимум.

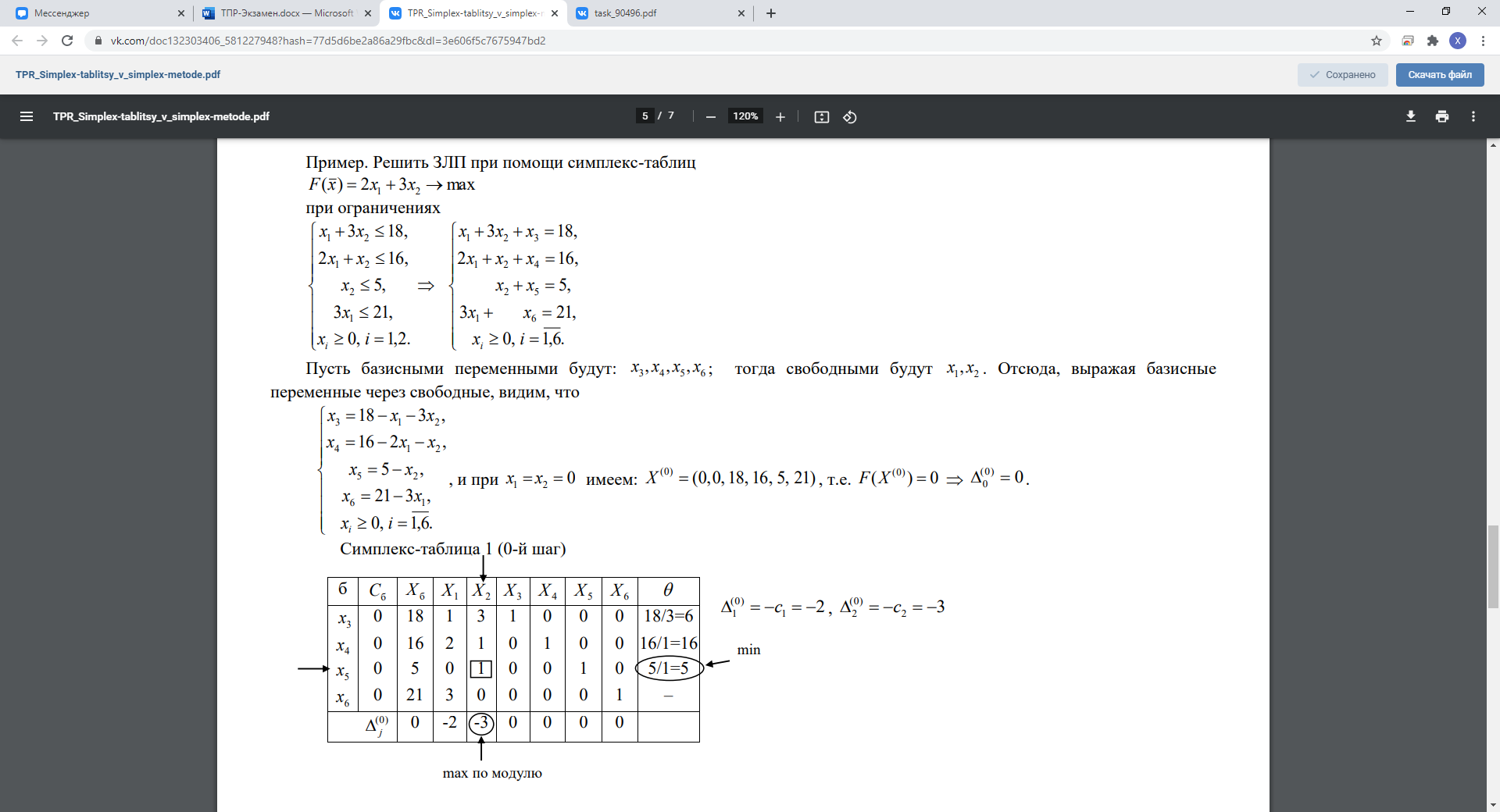
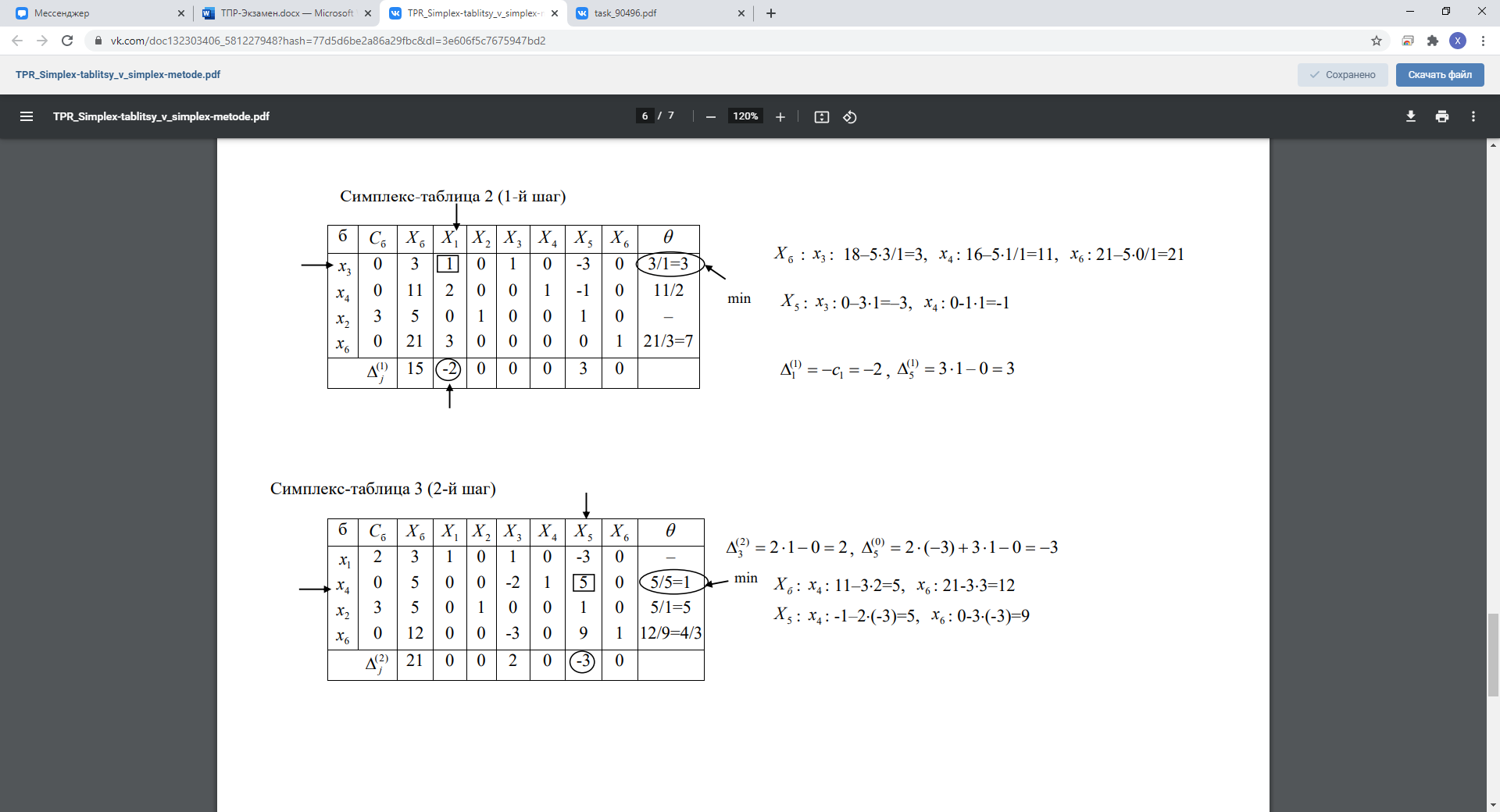
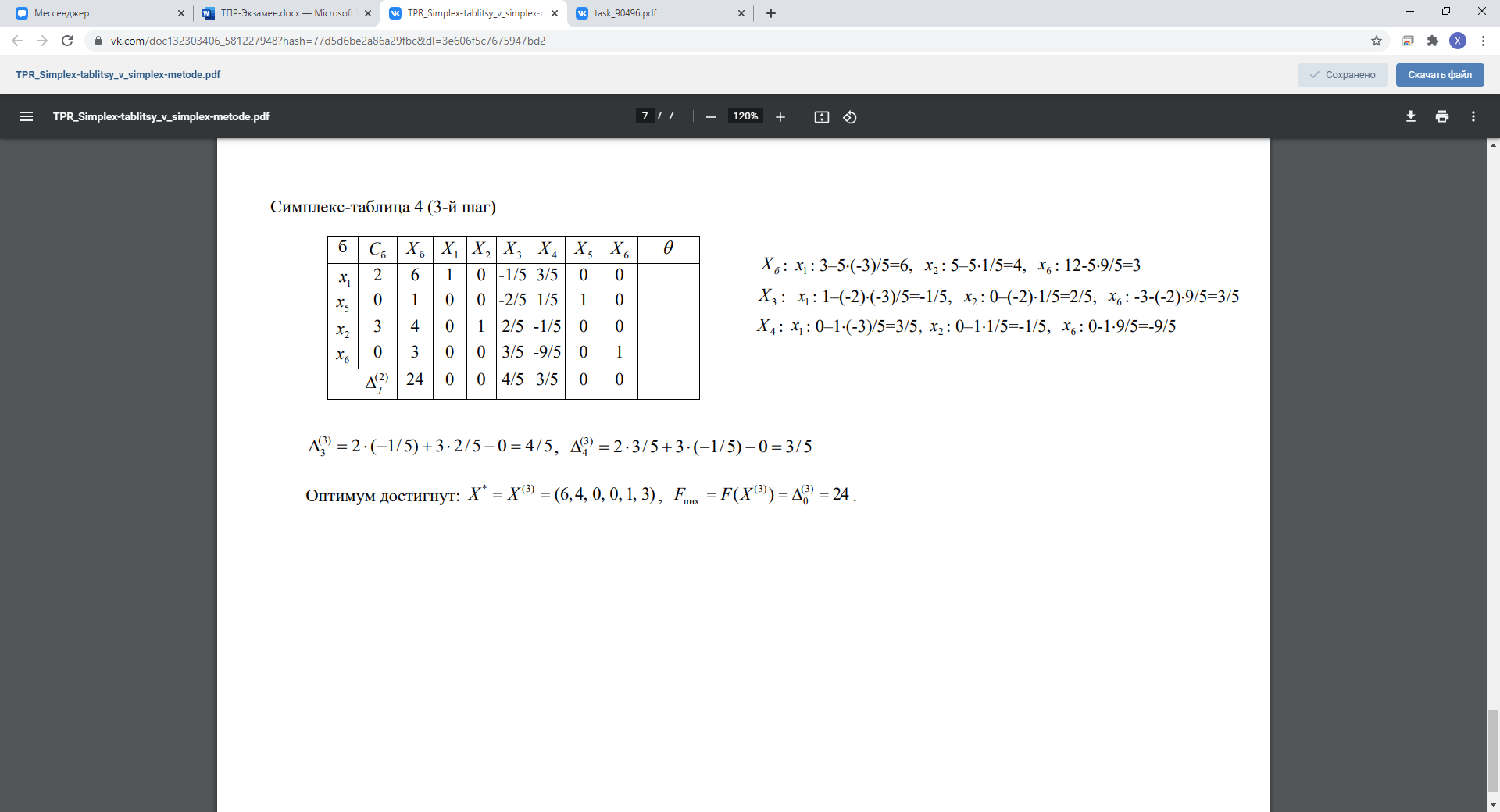
13. Метод искусственного базиса в симплекс-методе.

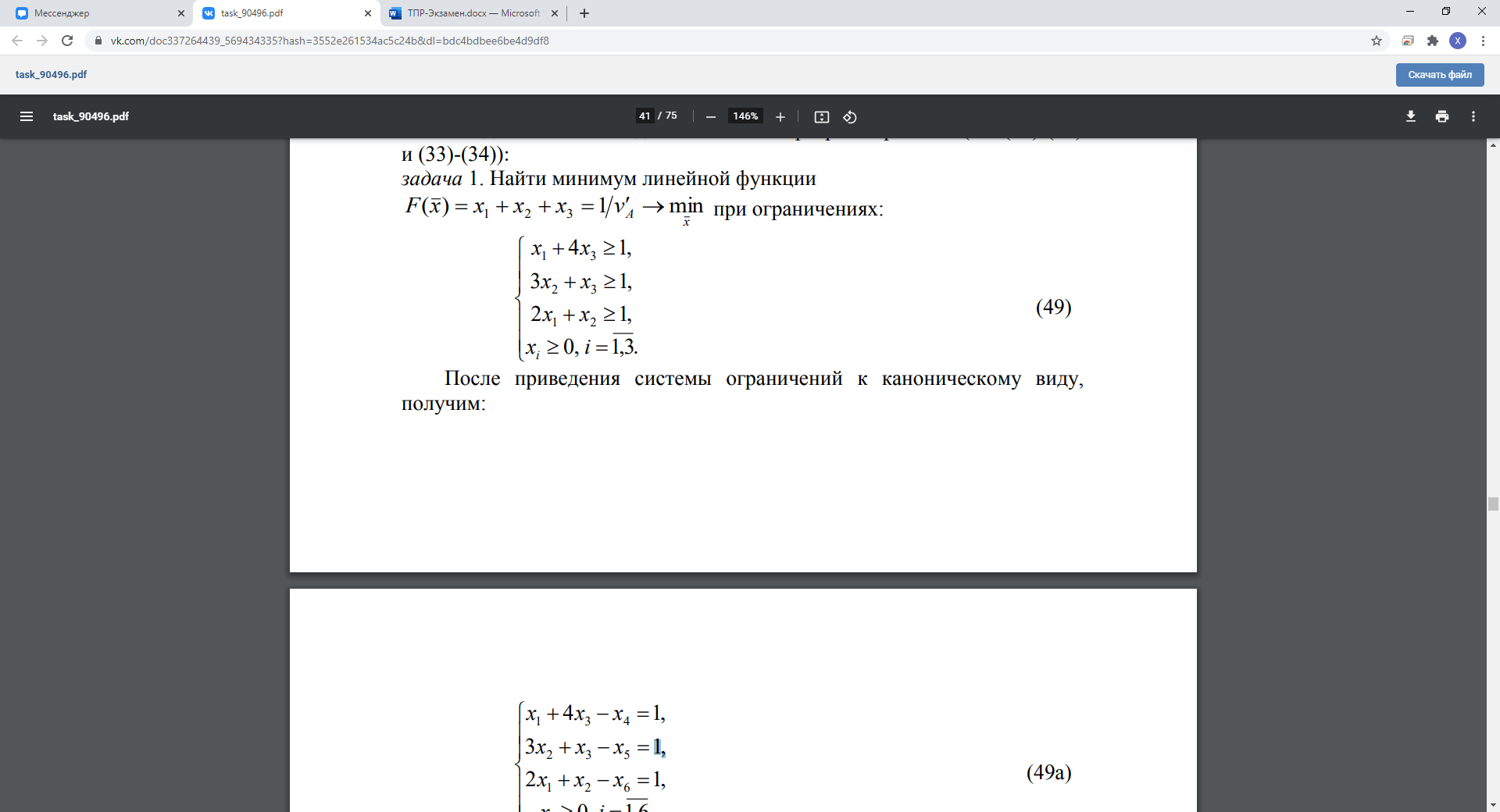
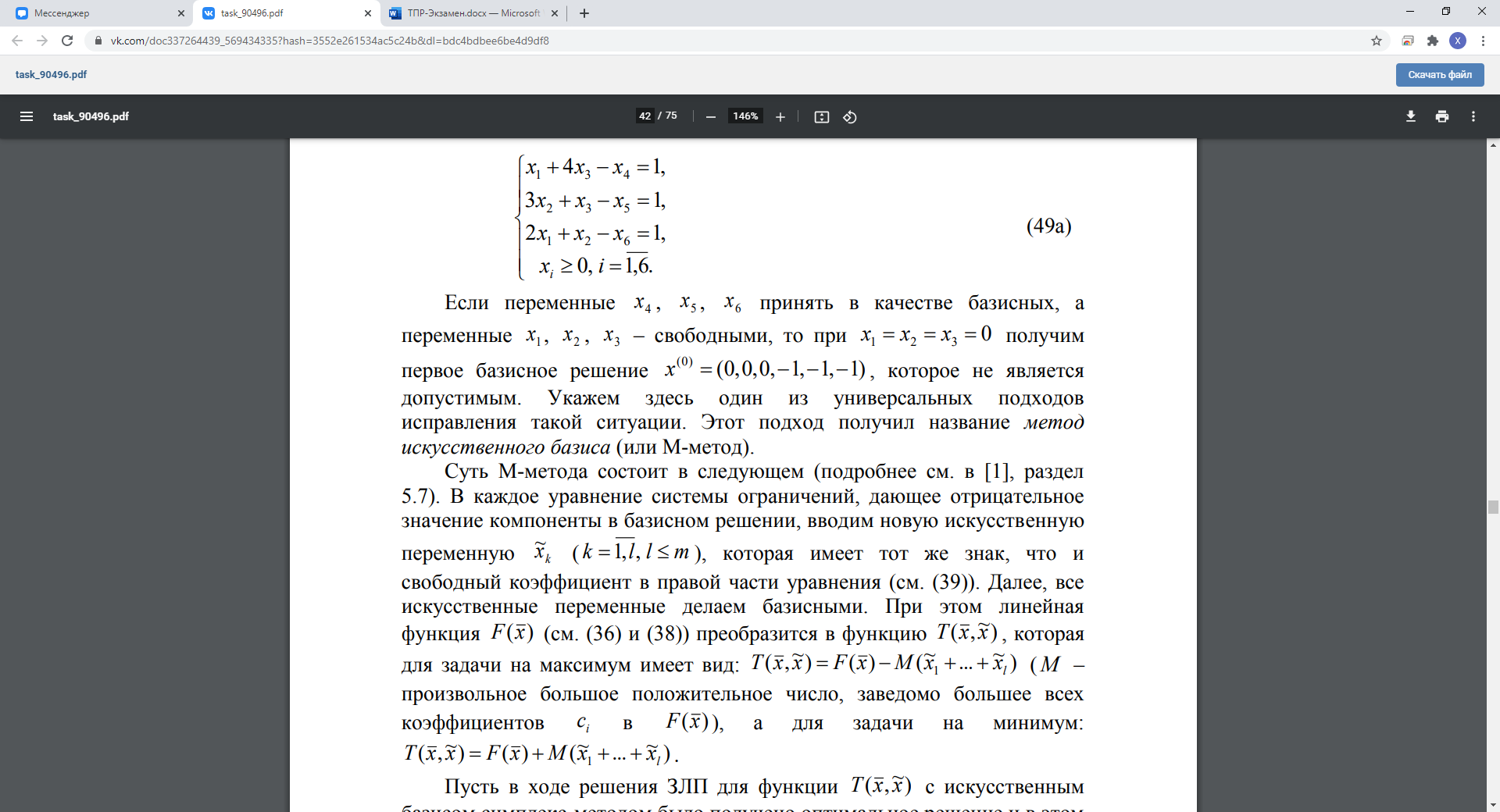
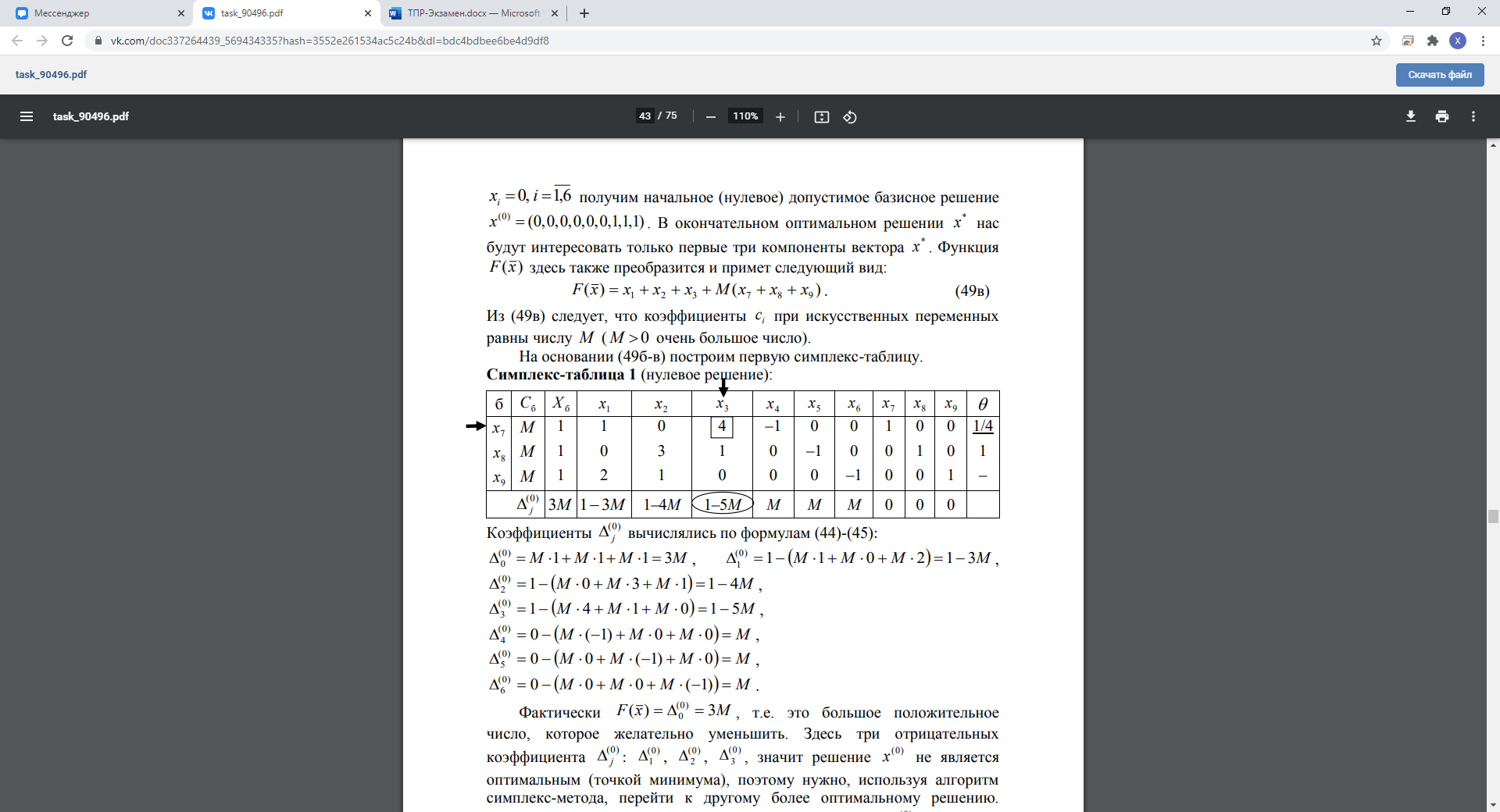
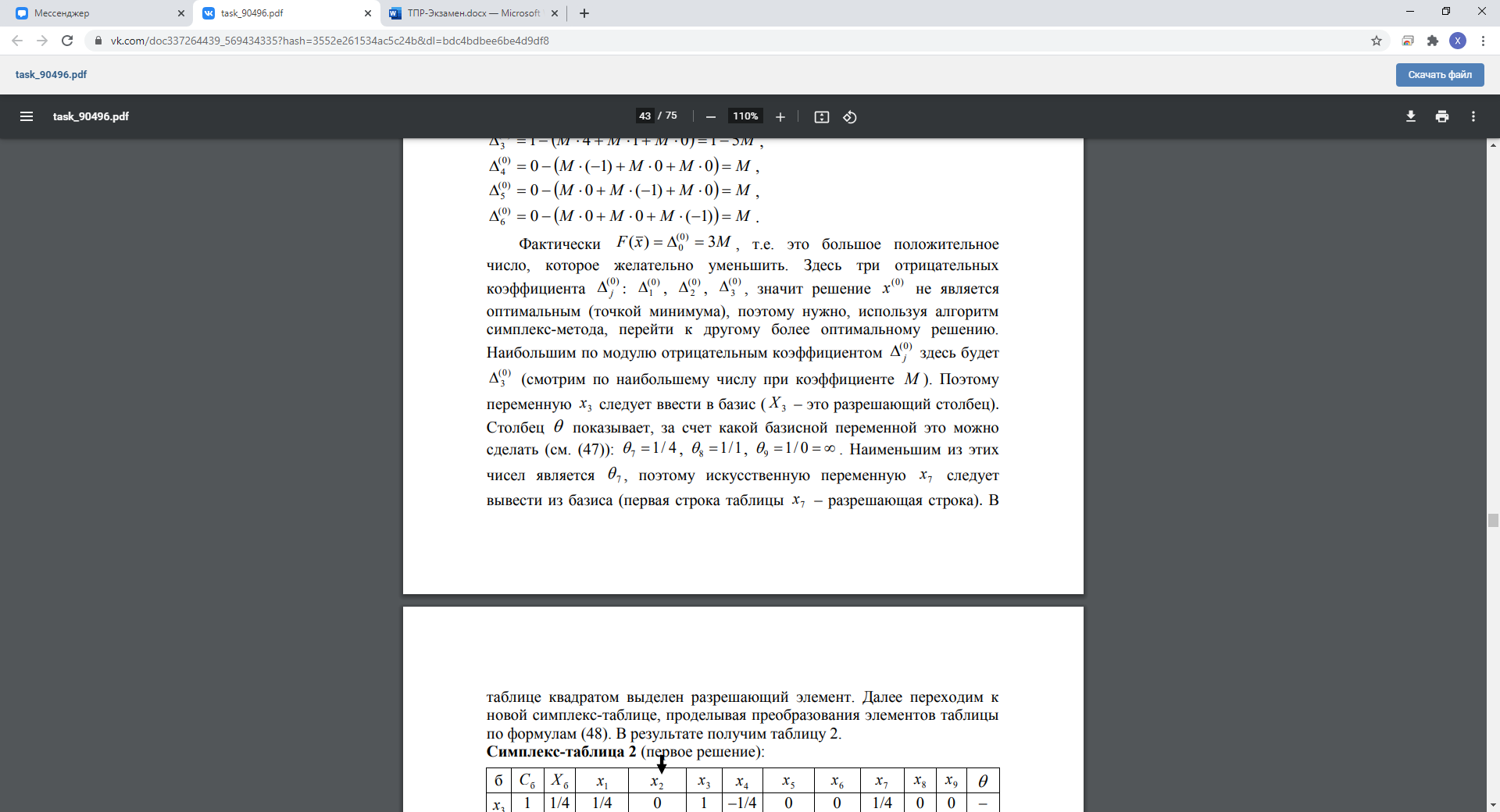
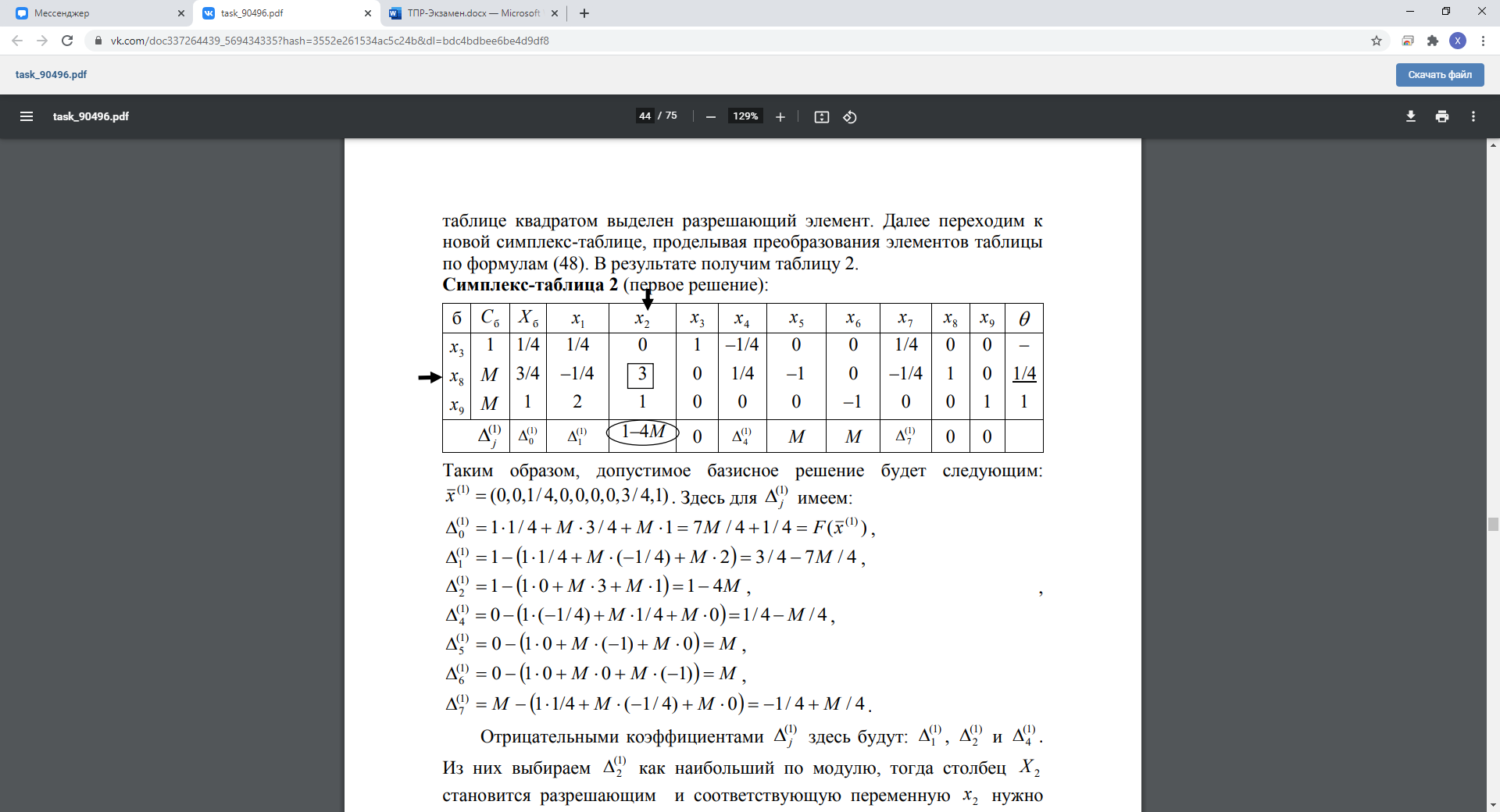
Дальше все как с обычными симплекс таблицами.

14. Двойственные задачи линейного программирования. Теоремы двойственности.

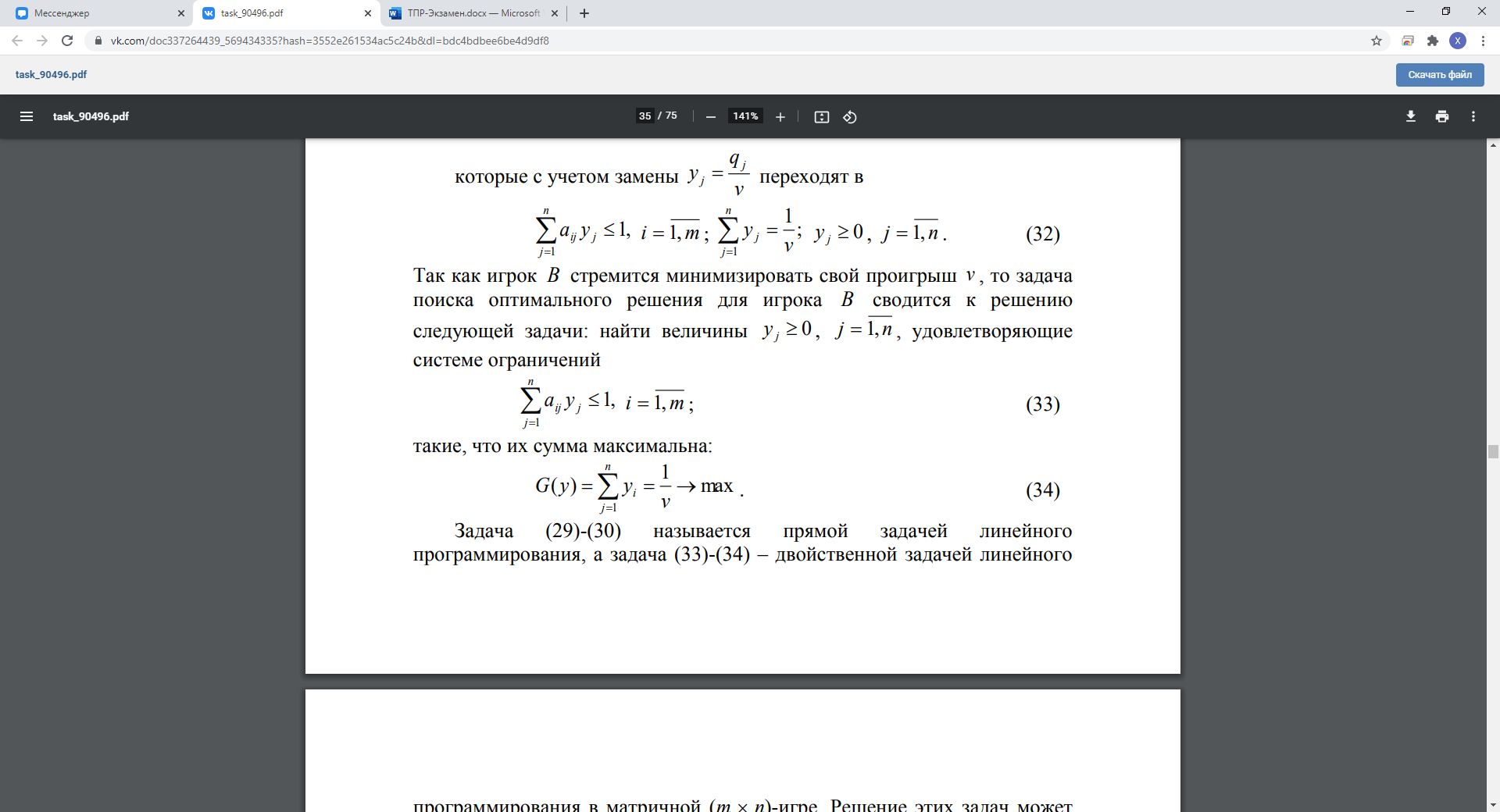
15. Антагонистические матричные игры. Примеры игр: игра в монету, поиск, игра полковника Блотто и др. Максимин и минимакс. Выигрыши двух игроков.

Антагонистической игрой называется некооперативная игра, в которой участвуют два или более игроков, выигрыши которых противоположны.

Матричная игра является антагонистической игрой. Первый игрок получает максимальный гарантированный (не зависящий от поведения второго игрока) выигрыш, равный цене игры, аналогично, второй игрок добивается минимального гарантированного проигрыша.

Под стратегией понимается совокупность правил (принципов), определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от сложившейся ситуации. Рассмотрим игру, в которой имеются два участника: первый игрок и второй игрок. Пусть в распоряжении первого игрока имеется m чистых стратегий, а в распоряжении второго игрока - n чистых стратегий. Поскольку рассматривается игра, естественно, что в этой игре есть выигрыши и есть проигрыши.

В платёжной матрице элементами являются числа, выражающие выигрыши и проигрыши игроков. Выигрыши и проигрыши могут выражаться в пунктах, количестве денег или в других единицах.

Составим платёжную матрицу:

.

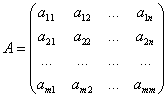Если первый игрок выбирает i-ю чистую стратегию, а второй игрок - j-ю чистую стратегию, то выигрыш первого игрока составит aij единиц, а проигрыш второго игрока - также aij единиц.

Так как aij + (- aij) = 0, то описанная игра является матричной игрой с нулевой суммой.

Как происходит выбор стратегии в матричной игре?

Вновь посмотрим на платёжную матрицу:

.

Сначала определим величину выигрыша первого игрока, если он использует i-ю чистую стратегию. Если первый игрок использует i-ю чистую стратегию, то логично предположить, что второй игрок будет использовать такую чистую стратегию, благодаря которой выигрыш первого игрока был бы минимальным. В свою очередь первый игрок будет использовать такую чистую стратегию, которая бы обеспечила ему максимальный выигрыш. Исходя из этих условий выигрыш первого игрока, который обозначим как v1, называется максиминным выигрышем или нижней ценой игры.

Теперь определим величину проигрыша второго игрока, если он использует j-ю стратегию. В этом случае первый игрок использует такую свою чистую стратегию, при которой проигрыш второго игрока был бы максимальным. Второй игрок должен выбрать такую чистую стратегию, при которой его проигрыш был бы минимальным. Проигрыш второго игрока, который обозначим как v2, называется минимаксным проигрышем или верхней ценой игры.

Простейшим примером матричной игры может служить бросание монеты. Правила игры следующие. Первый и второй игроки бросают монету и в результате выпадает "орёл" или "решка". Если одновременно выпали "орёл" и "орёл" или "решка" или "решка", то первый игрок выиграет одну единицу, а в других случаях он же проиграет одну единицу (второй игрок выиграет одну единицу). Такие же две стратегии и в распоряжении второго игрока. Соответствующая платёжная матрица будет следующей:

.

Игры Блотто (Игры Полковника Блотто) представляют собой класс игр двух лиц с нулевой суммой, в которой задача игроков состоит в распределении ограниченных ресурсов по нескольким объектам (полям битв). В классической версии игры игрок, выставивший больше ресурсов на поле, выигрывает битву на этом поле, а суммарный выигрыш (цена игры) равен сумме выигранных битв. Хотя игра полковника Блотто была впервые опубликована Борелем (Borel)^[1] в 1921-м году, большинство вариаций классической игры не были решены до 91-го года. В 2006-м году Роберсон (Roberson) описал равновесную цену классической игры для любого числа полей и любого уровня ресурсов, а также характеристические множества равновесия для большинства вариаций классической игры.^[2]

Игра названа в честь мифического Полковника Блотто из работы Гроса и Вагнера (Gross and Wagner) 1950-го года^[3]. Полковник был обязан найти оптимальное распределение своих солдат по N полям сражений, зная что:

1. на каждом поле сторона, выставившая больше солдат, выигрывает, но

2. ни одна сторона не знает, какое число солдат выставит противоположная сторона на каждом поле, и

3. обе стороны стремятся максимизировать число полей, на которых битва будет выиграна.

В качестве примера представим игру, в которой два игрока записывают три положительных целых числа в неубывающем порядке, сумма которых заранее задана (=S). Затем оба игрока сравнивают числа (по порядку). Игрок, у которого в двух позициях числа больше, выигрывает.

Для S = 6 возможны только три варианта: (2, 2, 2), (1, 2, 3) и (1, 1, 4). Легко видеть, что:

Любой триплет против такого же влечет ничью;

(1, 1, 4) против (1, 2, 3) влечет ничью;

(1, 2, 3) против (2, 2, 2) влечет ничью;

(2, 2, 2) бьёт (1, 1, 4).

Следовательно, (2, 2, 2) — оптимальная стратегия, поскольку выигрывает в одном случае, и не проигрывает во всех остальных. Однако, если оба игрока выберут стратегию (2, 2, 2) или (1, 2, 3), то ни один из игроков не сможет выиграть у другого меняя стратегию, так что каждая такая пара представляет собой Равновесие Нэша(Так называется набор стратегий в игре для двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники свои стратегии не меняют. Часто в играх с равновесием, изменение стратегии всех участников приведёт к увеличению выигрыша, но каждому отдельно взятому участнику игры невыгодно менять стратегию.).

При увеличении числа S становится все труднее провести анализ. Для S = 12 можно показать, что (2, 4, 6) является оптимальной стратегией, однако для S > 12, детерминированные стратегии не оптимальны. Для S = 13, выбирая (3, 5, 5), (3, 3, 7) и (1, 5, 7) с вероятностью 1/3 для каждой, оказывается оптимальной смешанной стратегией.

Для нахождения смешанных решений игры можно использовать метод переменного базиса, для чего используется приведение матричной игры к задаче линейного программирования. Получаемая матрица будет иметь большое количество строк и столбцов (равные числу стратегий), но хранить её не нужно — элементы матрицы можно получить в нужный момент программно. Размер базисной матрицы при этом будет небольшим.