
ИФПМ (ПРИТ) / Учебник
.pdf
Министерство образования и науки Российской Федерации Национальный исследовательский университет «МИЭТ»
А.В. Клюшин
Введение в дискретную математику
Учебное пособие
Утверждено редакционно-издательским советом университета
Москва 2014
УДК 519.7(075.8) К52
Рецензенты: докт. физ.-мат. наук, проф. И.Б. Кожухов; канд. техн. наук П.П. Усов
Клюшин А.В.
К52 Введение в дискретную математику: учеб. пособие. – 2-е изд. – М.: МИЭТ, 2014.
– 136 с.: ил.
ISBN 978-5-7256-0763-5
Изложены основные понятия и вопросы, относящиеся к дискретной математике:
множества и отображения, бинарные отношения, группы и поля, линейные коды, графы и алгоритмы, начальные понятия математической логики. После большинства параграфов даны задачи, позволяющие углубить понимание предмета.
Для студентов, изучающих дискретную математику.
ISBN 978-5-7256-0763-5 |
©МИЭТ, 2014 |
2
Учебное пособие
Клюшин Александр Викторович
Введение в дискретную математику
Редактор А.В. Тихонова. Технический редактор Л.Г. Лосякова. Корректор Л.Г. Лосякова. Верстка автора.
Подписано в печать с оригинал-макета 10.10.2014. Формат 60 84 1/16. Печать офсетная. Бумага офсетная. Гарнитура Times New Roman. Усл. печ. л. 7,89.
Уч.-изд. л. 6,8. Тираж 500 экз. Заказ 52.
Отпечатано в типографии ИПК МИЭТ.
124498, Москва, Зеленоград, проезд 4806, д. 5, МИЭТ.
3
Предисловие
Дискретная математика представляет собой область математики, в которой изуча-
ются свойства структур конечного характера, а также бесконечных структур, предпола-
гающих отделимость составляющих элементов. В отличие от дискретной математики классическая математика занимается преимущественно изучением свойств структур не-
прерывного характера. Эта особенность вытекает из топологии множества действитель-
ных чисел, в котором каждое число обладает системой окрестностей. С помощью тополо-
гии можно определить понятие предела, производной, интеграла и т.д. В дискретной математике топология дискретна, каждая точка обладает окрестностью, состоящей только из этой точки. В этом состоит существенное отличие от непрерывной математики.
Развитие дискретной математики обусловлено развитием компьютерной техники,
необходимостью создания средств обработки и передачи информации, а также представ-
ления различных моделей на компьютерах, являющихся по своей природе конечными структурами. Дискретная математика в последнее время стала обязательной составной ча-
стью технического образования. В МИЭТ дискретная математика читается на факультетах МПиТК, ЭКТ, ИТС, ПрИТ.
Настоящее учебное пособие отражает опыт чтения данного курса на факультетах ЭКТ и ИТС, однако его использование возможно и на других факультетах. Для более пол-
ного понимания излагаемого материала желательно, чтобы читатель был знаком с основа-
ми линейной алгебры.
Учебное пособие состоит из четырѐх глав. В главе «Алгебраические системы» рас-
смотрены бинарные отношения и их свойства, понятие группы. Большое внимание уделе-
но группам движений геометрических фигур на плоскости. Представлены группы авто-
морфизмов групп, приведѐн список групп до 10-го порядка. После общих определений кольца и поля описаны свойства конечных полей и способы их построения. Рассмотрено тело кватернионов.
Глава «Элементы теории кодирования» начинается с общих понятий линейных ал-
гебраических кодов, способов кодирования и декодирования. Далее даны коды Хэмминга,
циклические и БЧХ-коды.
В главе «Графы» после основных определений рассмотрены деревья, доказана тео-
рема о равносильных определениях дерева. Приведены некоторые алгоритмы на графах:
метод ветвей и границ и алгоритм Краскала. Изложены вопросы, связанные с фундамен-
тальными циклами и разрезами, использующимися в электротехнике, а также планарные графы, критерии планарности, алгоритм плоской укладки графа.
4
В главе «Элементы математической логики» описана техника, связанная с булевы-
ми функциями, доказан критерий Поста. Законы и свойства булевой алгебры разобраны вместе с примерами и приложениями.
В конце учебного пособия приведѐн список литературы, позволяющий заинтересо-
ванному читателю значительно выйти за пределы программы курса.
Автор выражает благодарность Булаховой Инге Витальевне за большую работу по подготовке рукописи к печати.
5
1.Алгебраические системы
1.1.Множества и отображения
Среди понятий дискретной математики базовыми являются понятия множества и отображения. Эти объекты обычно рассматриваются в начале первого семестра в курсе математического анализа. Однако имеет смысл рассмотреть их здесь более подробно.
«Наивное» определение множества заключается в том, что множество – это сово-
купность объектов произвольной природы. Сами объекты при этом называются элемента-
ми данного множества. Такое определение долгое время не имело никаких возражений.
Примерами множеств являются множество всех людей на планете, множество натураль-
ных чисел, множество студентов данной конкретной группы, множество групп на потоке и т.д. Последние два примера показывают, что само множество может служить элементом какого-то другого множества. Если никаких ограничений нет, то можно даже рассматри-
вать множества, которые являются элементами самих себя. Таким, например, должно быть множество всех множеств. Однако в начале этого века в математической печати ста-
ли появляться различные парадоксы, связанные с множествами и действиями над ними.
Один из наиболее известных – «парадокс Рассела». Он состоит в следующем.
Если допустимо рассматривать множества произвольной природы и, в частности,
такие, которые содержат сами себя в качестве элемента, разобьѐм все множества на два класса. К первому классу отнесѐм те множества, которые не содержат сами себя в качест-
ве элемента. Такие множества назовѐм собственными. К другому классу отнесѐм множе-
ства, которые содержат в качестве элемента сами себя. Их мы назовѐм несобственными.
Далее рассмотрим множество R всех собственных множеств. К какому классу относится само множество R ? Если оно собственное, то должно содержать само себя в качестве элемента, так как по своему определению оно содержит все собственные множества. Но тогда оно будет элементом самого себя, что противоречит определению первого класса собственных множеств. Допустим теперь, что множество R несобственное. Но оно со-
держит только собственные множества, поэтому множество R не является элементом са-
мого себя и, значит, его следует отнести к собственным множествам по определению пер-
вого класса. Опять противоречие.
Всѐ вышесказанное свидетельствует о том, что понятие множества далеко не такое простое, как это может показаться на первый взгляд. В частности, нельзя произвольно об-
разовывать множества, здесь нужны определѐнные правила. В дальнейшем такие правила были созданы, и соответствующая теория получила название теории классов. Мы будем
6

иметь дело в основном с конечными множествами. Несобственных множеств рассматри-
вать не будем, поэтому понятия множества как совокупность объектов для целей нашего курса будет достаточно.
Для числовых множеств будем использовать следующие общепринятые обозначе-
ния:
– множество всех натуральных чисел;
– множество всех целых чисел;
– множество всех рациональных чисел;
– множество всех действительных чисел;
– множество всех комплексных чисел.
Будем обозначать множества большими латинскими буквами A, B,..., Z . Элементы этих множеств будем, как правило, обозначать маленькими латинскими буквами a, b,..., z .
Тот факт, что a есть элемент множества A будем записывать с помощью следующего обозначения:
a A .
Задать множество означает описать, из каких элементов оно состоит. Если множе-
ство состоит из конечного, причѐм, небольшого числа элементов, то его часто задают
«списком». Например, запись A 1; 3; 5 означает, что множество A состоит из трѐх эле-
ментов 1, 3 и 5. Иногда для задания множества используется запись типа
A (x, y) 2 x2 y2 1 .
Она означает следующее: запись в фигурной скобке до вертикальной черты указы-
вает, откуда берутся элементы данного множества, а запись после вертикальной черты – какому свойству эти элементы удовлетворяют, т.е. берутся только те элементы, для кото-
рых высказывание после вертикальной черты оказывается верным. В данном примере множество A образуют все точки плоскости ( 2 обозначает множество всех точек плос-
кости), которые удовлетворяют уравнению x2 y2 1 . Другими словами, A – это окруж-
ность единичного радиуса с центром в начале координат. Иногда пишут просто
A (x, y) x2 y2 1 ,
если из контекста ясно, откуда берутся элементы (x, y) .
Определение 1. Если каждый элемент множества A принадлежит множеству
B , то будем говорить, что множество A вложено в множество B и обозначать
A B .
7

Если A B , но A B , будем говорить, что A – строгое подмножество множест-
ва B .
Определение 2. Пусть имеются два множества A и B . Их объединением будем называть множество, элементами которого являются все элементы множества A и
множества B . Объединение множеств A и B обозначается символом A B .
Определение 3. Пересечением множеств A и B будем называть множество,
элементами которого являются все элементы, принадлежащие A и B одновременно.
Пересечение множеств обозначается символом A B .
Определение 4. Разностью множеств A и B будем называть множество, со-
стоящее из всех тех элементов множества A , которые не принадлежат B . Разность множеств обозначается символом A \ B .
Определение 5. Множество, в котором нет элементов, будем называть пус-
тым и обозначать символом . Считается, что пустое множество является подмно-
жеством любого множества.
Определение 6. В случае если множество A конечно, число его элементов будем обозначать символом A . В случае, когда множество A бесконечно, будем писать A
.
Определение 7. Пусть все рассматриваемые множества содержатся в неко-
тором одном множестве X , которое будем называть универсальным, и A X – одно из них. Тогда множество X \ A будем называть дополнением множества A и обозначать символом A .
Например, если рассматриваются множества на плоскости, то роль X будет играть вся плоскость, а множество A будет состоять из всех точек плоскости, не принадлежащих
A .
Определение 8. Пусть имеются два множества A и B . Их декартовым произ-
ведением будем называть множество A B , элементами которого являются пары (a, b) ,
где a A, b B . Если имеется n множеств A1, A2 ,..., An , то аналогично можно образовать их декартово произведение
A1 ... An (a1,..., an ) ai Ai ; i 1,..., n .
Если множества A и B конечны, то A B A B . Аналогично, если множества A1,..., An конечны, то A1 ... An A1 ... An .
Например, если множество A x, y , а множество B 1, 2, 3 , то множество A B
состоит из 6 элементов: (x;1) , (x; 2) , (x; 3) , ( y;1) , ( y; 2) , ( y; 3) .
8
Определение 9. Пусть имеются два множества A и B . Если каждому элемен-
ту a A поставлен в соответствие какой-то элемент b B , то говорят, что задано отображение f из множества A в множество B . Этот факт обозначается следую-
щим образом:
f : A B .
Если элементу a A поставлен в соответствие элемент b B , то b называют
образом элемента a и обозначают символом f (a) . Элемент a при этом называют про-
образом элемента b .
Каждый элемент при отображении f имеет ровно один образ, в то время как эле-
мент множества B может иметь несколько прообразов. Множество прообразов может
быть также и пустым.
Задать отображение означает, во-первых, указать множества A и B и, во-вторых,
каким-то образом определить элемент f (a) для каждого элемента a A .
Приведѐм некоторые примеры отображений.
Пример 1. |
f : , |
f (n) 2n . |
Здесь для каждого элемента n элемент f (n) определѐн формулой. Например, |
||
f (3) 6, f ( 4) 8, |
f (0) 0 . |
|
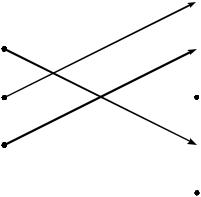
Пример 2. |
f : A B, |
A a, b, c , B , , , , . |
a |
|
b |
|
c |
|
|
|
Здесь образ каждого элемента из множества |
A определѐн стрелочкой. Например, |
f (c) . |
|
9
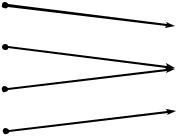
Пример 3. f : A B, A a, b, c, d , B , , .
a
 α
α
b
 β
β
c
 γ
γ
d
Определение 10. Отображение f : A B называется взаимно однозначным, ес-
ли
1) образы различных элементов из множества A различны, т.е. если a1 a2 , то и
f(a1) f (a2 ) ;
2)для любого элемента b B найдѐтся элемент a A такой, что f (a) b .
Отображение f из примера 2 удовлетворяет условию 1), однако не удовлетворяет
условию 2). Отображение f из примера 3, напротив, удовлетворяет условию 2), но не
удовлетворяет условию 1).
Если множества A и B конечны и существует взаимно однозначное отображение f : A B, то отсюда, очевидно, следует, что количество элементов в множествах A и B
одно и то же. Для бесконечных множеств, однако, взаимно однозначное отображение
f : A B |
может существовать даже если A |
– |
строгое подмножество в |
B . Например, |
|
A 0, 1 |
– множество действительных чисел из отрезка 0, 1 , B 0, 2 , f : A B опреде- |
||||
лено формулой f (x) 2x . |
|
|
|
|
|
Определение 11. Пусть A 1, 2,..., n . |
Отображение f : A A , |
для которого |
|||
f (k) ik , |
k 1,..., n , можно представить следующей таблицей: |
|
|||
|
1 |
2 |
... |
n |
|
|
f |
i2 |
|
. |
|
|
i1 |
... |
in |
|
|
Взаимно однозначное отображение f : A A будем называть подстановкой. |
|||||
Определение 12. Если имеются отображения f : A B и g : B C , то можно |
|||||
образовать отображение gf : A C . При этом полагаем (gf )(x) g( f (x)) |
для всех x A . |
||||
Отображение gf будем называть суперпозицией отображений f и g .
Как следует из определения, суперпозиция двух отображений всегда действует справа налево, т.е. чтобы найти (gf )(x) , нужно сначала к элементу x применить отобра-
жение f , а потом g .
10
