
ИФПМ (ПРИТ) / Учебник
.pdf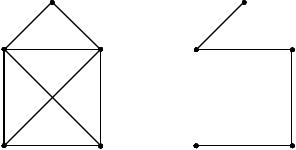
4.
|
1 |
2 |
3 |
4 |
5 |
1 |
|
15 |
47 |
20 |
7 |
2 |
8 |
|
17 |
1 |
4 |
3 |
26 |
4 |
|
40 |
9 |
4 |
25 |
5 |
29 |
|
7 |
5 |
17 |
2 |
17 |
16 |
|
3.7. Фундаментальные циклы и разрезы
Техника теории графов используется при анализе электрических цепей. Законы Кирхгофа для токов и напряжений приводят к задачам, эффективно решаемым на языке теории графов. Напомним, что остовом связного графа G называется подграф G , содер-
жащий все вершины графа G и являющийся деревом.
Определение 1. Пусть T – остов связного графа G . Тогда рѐбра, принадлежа-
щие остову, называются ветвями, а не принадлежащие – хордами.
Пусть G – связный граф, а T – некоторый его фиксированный остов. Обозначим ветви графа b1,b2 ,...,bn 1, а хорды c1,c2 ,...,cm n 1 , где m – число рѐбер, а n – число вершин графа G . Если к остову прибавить одну из хорд ci , то получится ровно один цикл, кото-
рый обозначим Ci .
Определение 2. Цикл связного графа G с фиксированным остовом T , содер-
жащим ровно одну хорду, называется фундаментальным.
Число фундаментальных циклов равно числу хорд, т.е. m n 1 .
Пример 1. Рассмотрим следующий граф G и остов T :
|
Граф G |
Остов T |
Здесь n 5, |
m 8 . Число фундаментальных циклов |
равно m n 1 8 5 1 4 . Вот |
они:
71

C1 |
C2 |
C3 |
C4 |
Следует отметить, что среди всех фундаментальных циклов только один содержит |
|||
хорду c1 , только один содержит хорду c2 |
и т.д. |
|
|
Определение 3. Разрезающим множеством связного графа G называется та- |
|||
кое множество его рѐбер, удаление которых делает граф |
G несвязным. Разрезающее |
||
множество, не содержащее собственных разрезающих подмножеств, называется разре-
зом. Если выбран некоторый остов T графа G , то разрез, содержащий ровно одну ветвь, называется фундаментальным.
Количество фундаментальных разрезов равно количеству ветвей, т.е. n 1. После удаления одной из ветвей bi из остова T последний распадается на две компоненты связ-
ности T1 и T2 . Тогда i -й фундаментальный разрез будет состоять из ветви bi и всех хорд графа G , соединяющих вершину из T1 с вершиной из T2 .
Пример 1 (продолжение). Число фундаментальных разрезов графа G равно n 1 4 . Вот они:
|
|
K1 |
K2 |
K3 |
|
|
K4 |
|
|
Определение 4. Пусть G(V , E) – связный граф, V1 V , |
|
|
|
||
|
|
V1 V \V1 . Разделителем |
|||||
|
|
|
|||||
V1,V1 графа G называется множество всех рѐбер из E , оба конца которых принадле- |
|||||||
жат V1 . Тогда подграф G1(V1, E1) графа G называется вершинно порождѐнным и обозна- |
|||||||
чается V1 . |
|
|
|
|
|
||
|
|
Теорема 1. Пусть G(V , E) |
– граф, в котором каждая вершина имеет чѐтную |
||||
степень. Тогда множество рѐбер |
E графа G можно представить в виде объединения |
||||||
рѐберно непересекающихся циклов.
Доказательство. Индукция по числу рѐбер. Основанием индукции служит граф с пустым множеством рѐбер.
72

Пусть для графов с числом рѐбер меньше m утверждение теоремы верно. Рассмот-
рим граф, для которого |
|
E |
|
m . Возьмѐм произвольную вершину v1 и инцидентное ей реб- |
|
|
|||
|
|
|||
ро (v1,v2 ) . Вершина v2 |
|
инцидентна другому ребру (v2 ,v3 ) , отличному от предыдущего. |
||
Продолжим этот процесс до того момента, когда дойдѐм до вершины vk , которая уже встречалась ранее. Этот момент наступит в силу конечности множества V . Тогда рѐбра
(vk ,vk 1), (vk 1,vk 2 ),..., (vk l ,vk ) образуют простой цикл. Удалим рѐбра этого цикла из графа
G . Поскольку каждая вершина, входящая в этот цикл, инцидентна двум рѐбрам цикла, в
полученном графе степени всех вершин по-прежнему останутся чѐтными, и утверждение
верно по предположению индукции. |
|
|
|
|
|
|
|||||||||||||||||||||||||||
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Теорема 2. Разделитель |
|
|
|
|
|
связного графа |
|
G является разрезом графа |
|||||||||||||||||||||||||
V1,V1 |
|
||||||||||||||||||||||||||||||||
G V1 |
и |
|
|
|
|
|
– связные подграфы графа G . |
|
|
|
|
|
|||||||||||||||||||||
V1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Если S |
|
– разрез связного графа G , а V1 – множество вершин одной компоненты |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
связности графа G \ S , то S V1,V1 . |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Доказательство. |
Пусть |
R V1,V1 |
– |
разделитель, |
являющийся разрезом. Допус- |
||||||||||||||||||||||||||||
тим, что |
V |
|
|
|
не является связным подграфом. Пусть V 1 |
– множество вершин одной из |
|||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
компонент связности графа |
|
V1 . Рассмотрим множество R1 всех рѐбер из R , один из кон- |
|||||||||||||||||||||||||||||||
цов которых лежит в V 1 |
. Заметим, |
что в G не может существовать рѐбер, соединяющих |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вершины из V 1 с вершинами из |
V \V1 , иначе |
V 1 |
не был бы компонентой связности гра- |
||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||
фа V1 , ведь граф |
V1 |
содержит все рѐбра из G , оба конца которых принадлежат V1 . |
|||||||||||||||||||||||||||||||
Множество |
R1 |
является разрезающим, поскольку любой путь, соединяющий вер- |
|||||||||||||||||||||||||||||||
шины из V 1 |
|
с вершинами из |
|
V |
, содержит рѐбра из R . Поскольку в R содержатся также |
||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
рѐбра, соединяющие V \V1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
с |
V , ведь граф является связным, то множество рѐбер R явля- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||
ется собственным подмножеством в R , что противоречит тому, что R является разрезом. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Значит, |
V1 |
– связный подграф. Аналогично связен граф V1 . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Обратно. Пусть V1 |
и V1 |
|
– связные подграфы. Если R1 – собственное подмноже- |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
ство в R V1,V1 |
, |
то после удаления множества рѐбер R1 |
останется хотя бы одно ребро, |
||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
соединяющее V1 |
и V1 , |
следовательно, получившийся граф G1(V , E \ R1) по-прежнему будет |
|||||||||||||||||||||||||||||||
связным. Значит, |
R – разрез. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
73
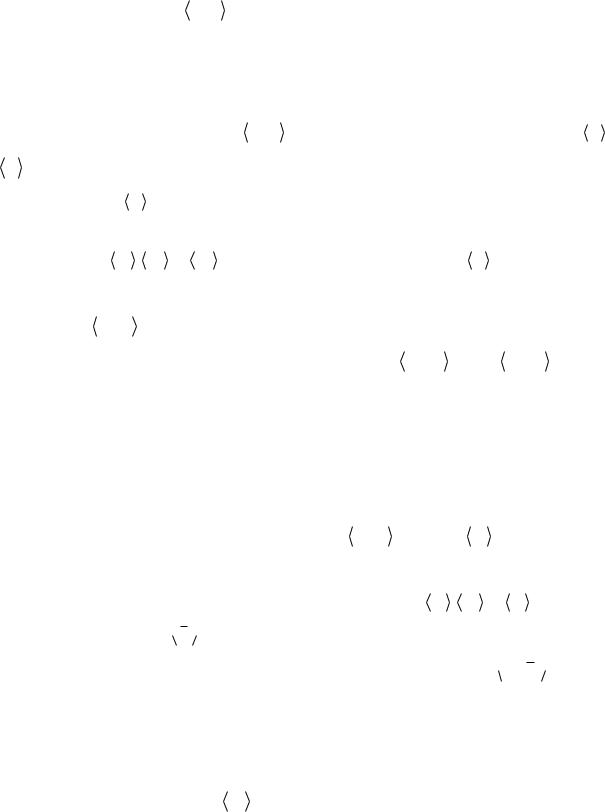
|
|
|
Пусть теперь |
S – разрез связного графа G , а V1 – множество вершин одной из |
||||||||||||||||||||||
компонент связности графа G1(V , E \ S) . |
Тогда один из концов рѐбер из S лежит в V1 , а |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
другой – в V1 . Поэтому S V1,V1 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Теорема 3. |
|
Любой разделитель связного графа G(V , E) является разрезом или |
|||||||||||||||||||||
объединением рѐберно непересекающихся разрезов. |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Доказательство. Пусть S V1,V1 |
– разделитель, где V1 V , V1 V \V1 . Если |
V1 и |
|||||||||||||||||||||
|
|
|
– связные подграфы, то разделитель S является разрезом в силу теоремы 2. |
|
||||||||||||||||||||||
V1 |
|
|||||||||||||||||||||||||
|
|
|
Допустим, |
|
|
V1 |
не является связным подграфом. Тогда множество вершин V1 |
мож- |
||||||||||||||||||
но |
представить |
в |
виде |
объединения таких попарно непересекающихся подмножеств |
||||||||||||||||||||||
A1, A2 ,..., Ak , что A1 |
, |
A2 |
,..., Ak – компоненты связности подграфа V1 |
. Заметим, что в G |
||||||||||||||||||||||
не может существовать рѐбер, соединяющих Ai |
и Aj при i j . Поэтому любое ребро раз- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
делителя S1 A1, |
A1 |
|
соединяет вершины из A1 |
с вершинами из V1 , а значит, принадлежит |
||||||||||||||||||||||
|
S1 S . Аналогично, |
|
|
|
|
|||||||||||||||||||||
S . Таким образом, |
разделители S2 A2 , |
A |
2 ,..., Sk |
Ak , |
A |
k являются |
||||||||||||||||||||
подмножествами в S , причѐм S S1 S2 ... Sk . Итак, разделитель S |
представлен в виде |
|||||||||||||||||||||||||
объединения рѐберно непересекающихся разделителей, у которых первое множество вершин вершинно порождает связный подграф. Покажем теперь, что каждый из разделителей Si является разрезом или может быть представлен в виде объединения рѐберно непересе-
кающихся разрезов. |
|
|
|
|
|
|
|
|
||
|
|
|
Si |
|
|
|
|
|
|
|
Действительно, пусть для разделителя |
Ai , Ai подграф |
Ai |
не является связ- |
|||||||
|
|
|
|
|||||||
ным подграфом. Тогда множество вершин Ai |
можно представить в виде объединения по- |
|||||||||
парно непересекающихся подмножеств B1, B2 ,..., Bi |
таких, что B1 , |
B2 |
,..., Bi – компонен- |
|||||||
ты связности подграфа  Ai
Ai  . Так же как и ранее, в G не может существовать рѐбер,
. Так же как и ранее, в G не может существовать рѐбер,
соединяющих Bi и B j при i j . Поэтому любое ребро разделителя Sij  Bj , Bj
Bj , Bj  соединяет
соединяет
вершины из B j с вершинами из Ai , а значит, принадлежит Si . Таким образом, Sij Si . За-
метим, что для любого s 1,...,l |
в G существуют рѐбра, соединяющие Ai и Bs , |
так как G |
|||||
|
|
|
|
|
|
||
является связным графом. Для любого j множество B j состоит из оставшихся Bi |
(кроме |
||||||
i j ) и множества Ai . Поэтому |
|
|
|
||||
B j является связным подграфом. Следовательно, разде- |
|||||||
лители Sij являются разрезами и Si Si1 Si2 ... Sil . Поэтому и разделитель |
S |
можно |
|||||
представить в виде объединения рѐберно непересекающихся разрезов. |
|
|
|||||
Теорема доказана. |
|
|
|
|
|
|
|
|
74 |
|
|
|
|
||
Теорема 4. Любые цикл и разрез связного графа имеют чѐтное число общих рѐ-
бер.
Доказательство. В силу теоремы 2 данного параграфа любой разрез S является разделителем  V1,V1
V1,V1  . Пусть одна из вершин цикла принадлежит V1 . Если в процессе про-
. Пусть одна из вершин цикла принадлежит V1 . Если в процессе про-
хождения данного цикла попадаем в V1 (по одному из рѐбер множества S ), то необходимо вернуться в V1 (так же по ребру из S ). Поэтому число общих рѐбер цикла и разреза долж-
но быть чѐтным.
Теорема доказана.
3.8. Линейные пространства, связанные с графами
|
Определение 1. Пусть G(V , E) – |
некоторый граф, и |
E1 E . Пусть V1 V |
– |
|||||||
множество всех вершин из V , для каждой из которых найдѐтся ребро из E1 , |
которому |
||||||||||
эту вершина инцидентна. Тогда подграф G1(V1, E1) называется рѐберно порождѐнным |
|||||||||||
подграфом и обозначается E1 . |
|
|
|
|
|
|
|
|
|||
|
Всякий подграф графа G , не содержащий изолированных вершин, является рѐбер- |
||||||||||
но порождѐнным своим множеством рѐбер. |
|
|
|
|
|
|
|||||
|
Определение 2. Пусть G1(V1, E1) , G2 (V2 , E2 ) – два подграфа графа G . Их кольце- |
||||||||||
вой |
суммой |
называется |
подграф, |
рѐберно |
порождѐнный |
множеством |
|||||
E1 E2 |
(E1 \ E2 ) (E2 \ E1) . Кольцевая сумма обозначается G1 G2 . |
|
|
|
|
||||||
|
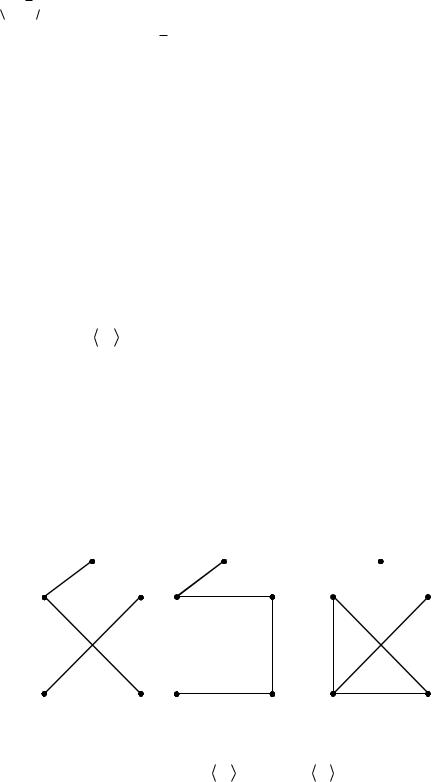
Пример |
1. Приведѐм |
|
пример |
двух |
подграфов |
графа |
G |
и |
их |
|
суммы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G1 |
G2 |
G1 G2 |
Определение 3. Пусть G(V , E) – граф. Перенумеруем его рѐбра: E e1,e2 ,...,em . |
||
Каждому рѐберно порождѐнному подграфу |
E |
(включая ) графа G сопоставим по- |
следовательность ( 1,..., m ) из 0 и 1 длины |
m . А именно, i 1, если ei E и i 0 в |
|
противном случае. Множество всех таких последовательностей обозначим WG .
75
Множество WG с операцией покомпонентного сложения по модулю 2 является ли-
нейным пространством над полем 2 . Операция умножения на элементы поля 2 опреде-
ляется очевидным образом: при умножении на 0 вектор обнуляется, при умножении на 1
вектор не меняется. Сумме элементов из WG соответствует сумма подграфов.
В дальнейшем будем отождествлять множество таких последовательностей и множество подграфов графа G . (Точнее, эти пространства изоморфны.)
Определение 4. Пусть G(V , E) – граф. Множество всех векторов ( 1,..., m )
пространства WG , соответствующих всем циклам (включая пустой) графа G и объеди-
нениям рѐберно непересекающихся циклов, обозначим WC . Множество всех векторов
( 1,..., m ) пространства WG , соответствующих всем разрезам (включая пустой)
графа G и объединениям рѐберно непересекающихся разрезов, обозначим WS .
Теорема 1. Кольцевая сумма двух циклов является циклом или объединением рѐ-
берно непересекающихся циклов.
Доказательство. Каждая вершина, входящая в цикл, имеет чѐтную степень (если цикл простой, то степень каждой вершины равна двум). При сложении двух циклов оди-
наковые рѐбра удаляются, при этом степень каждой концевой вершины уменьшается на 2,
т.е. остаѐтся чѐтной. Поэтому сумма двух циклов представляет собой цикл или объедине-
ние рѐберно непересекающихся циклов в силу теоремы 1 § 3.7.
Теорема доказана.
Следствие. Множество всех циклов (включая пустой) и объединений рѐберно не-
пересекающихся циклов образует линейное подпространство пространства WG .
Определение 5. Подпространство, указанное в следствии, будем называть под-
пространством циклов и обозначать WC .
Теорема 2. Кольцевая сумма двух разделителей также является разделителем.
Кольцевая сумма двух разрезов является разрезом или объединением рѐберно непересе-
кающихся разрезов. |
|
|
|
|
|
Доказательство. |
Пусть |
S1 (A, B), S2 |
(C, D) |
– |
разделители, где |
A B C D , A B C D V . |
При сложении |
S1 S2 |
рѐбра, соединяющие A C с |
||
A D , исчезают. Таким образом, S1 S2 является разделителем, |
состоящим из рѐбер, со- |
||||
единяющих (A C) (B D) |
с (B C) (A D) . Каждый разрез является разделителем, |
||||
поэтому сумма двух разрезов также будет разделителем, который будет разрезом или объ-
единением рѐберно непересекающихся разрезов в силу теоремы 3 § 3.7.
Теорема доказана.
76
Следствие. Множество всех разрезов (включая пустой) и объединений рѐберно не-
пересекающихся разрезов образует линейное подпространство пространства WG .
Определение 6. Подпространство, указанное в следствии, будем называть под-
пространством разрезов и обозначать WS . |
|
|
|
|
|
|
|
|
|
|
Теорема 3. Пусть G(V , E) |
– связный граф, |
|
V |
|
n, |
|
E |
|
m , T – остов графа G . То- |
|
|
|
|
|
|||||||
гда фундаментальные циклы относительно T |
образуют базис пространства циклов. Та- |
|||||||||
ким образом, dimWC m n 1. |
|
|
|
|
|
|
|
|
|
|
Доказательство. Пусть |
e1,...,em n 1 |
– хорды графа G относительно T и |
||||||||
C1,...,Cm n 1 – соответствующие фундаментальные циклы. Каждый фундаментальный цикл содержит ровно одну хорду графа G . Поэтому фундаментальные циклы линейно незави-
симы. Пусть C – произвольный цикл, содержащий хорды ei |
|
,...,ei . Рассмотрим объедине- |
||||||||
|
1 |
|
k |
|
||||||
ние фундаментальных циклов C Ci |
... Ci . Если C C , |
то C C содержит непустой |
||||||||
1 |
k |
|
|
|
||||||
цикл, а значит, хорду графа G , что является противоречием, так как хорды ei |
,...,ei отсут- |
|||||||||
|
|
|
|
|
|
|
|
1 |
k |
|
ствуют в графе C C , а других хорд этот граф содержать не может. |
|
|||||||||
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
Теорема 4. Пусть G(V , E) – связный граф, |
|
V |
|
n, |
|
E |
|
m , T – остов графа G . То- |
||
|
|
|
|
|||||||
гда фундаментальные разрезы относительно T образуют базис пространства разрезов. |
||||||||||
Таким образом, dimWS n 1 . |
|
|
|
|
|
|
|
|
|
|
Доказательство. Пусть f1,..., |
fn 1 – ветви графа G относительно T и |
K1,..., Kn 1 – |
||||||||
соответствующие фундаментальные разрезы. Каждый фундаментальный разрез содержит ровно одну ветвь графа G . Поэтому фундаментальные разрезы линейно независимы.
Пусть K – произвольный разрез, содержащий ветви ai1 ,..., fik . Рассмотрим объединение фундаментальных разрезов K Ki1 ... Kik . Если K K , то K K содержит непустой разрез, а значит, ветвь графа G, что является противоречием, так как ветви fi1 ,..., fik отсут-
ствуют в графе C C , а других ветвей этот граф содержать не может.
Теорема доказана.
Теорема 5. Пространства WC и WS ортогональны.
Доказательство. Действительно, каждый цикл и каждый разрез имеют чѐтное число общих рѐбер.
77
3.9.Матрицы, связанные с графами
Вэтом параграфе наряду с неориентированными графами будем рассматривать ориентированные графы, которые будем называть орграфами. Граф G всегда обозначает граф без петель на n вершинах и m рѐбрах.
Определение 1. Пусть G(V , E) – граф. Перенумеруем его вершины: V v1,...,vn .
Матрицу A (aij ) размера n n , в которой
1, если вершины ai и a j соединены ребром;
aij
0 в противном случае,
будем называть матрицей смежности графа G .
Предложение 1. Пусть G(V , E) – граф, в котором вершины перенумерованы и A –
его матрица смежности. Тогда элемент aij(k ) матрицы Ak равен числу маршрутов между вершинами vi и v j длины k .
Определение 2. Пусть G(V , E) – граф, на каждом ребре которого задано на-
правление. Такой граф будем называть орграфом. Рѐбра орграфа будем называть дугами.
Если направление на дуге e (vi ,v j ) задано от вершины vi к вершине v j , то будем гово-
рить, что дуга e исходит из вершины vi |
и заходит в вершину v j . |
|
|
|||
Определение 3. Пусть G(V , E) |
– орграф, в котором перенумерованы вершины и |
|||||
дуги. Матрицей инцидентности графа |
G называется матрица B (bij ) размера |
n m , |
||||
элементы которой определяются следующим образом: |
|
|
||||
1, если j-я дуга инцидентна |
i-й вершине и исходит |
из неѐ; |
|
|||
|
j-я |
|
|
i-й вершине и заходит |
|
|
bij 1, если |
дуга |
инцидентна |
в неѐ; |
|
||
|
j-я |
дуга не инцидентна i-й вершине. |
|
|
||
0, если |
|
|
||||
Всякий столбец матрицы B орграфа содержит два ненулевых элемента –1 и 1. По-
этому любую строчку этой матрицы можно определить по остальным (n 1) строкам.
Определение 4. Матрицу B0 , полученную из матрицы B вычѐркиванием одной произвольной строки, будем называть усечѐнной матрицей инцидентности.
Очевидно, ранги матриц B и B0 совпадают и не превосходят n 1.
Теорема 1. Определитель любой усечѐнной матрицы инцидентности дерева ра-
вен 1.
Доказательство. Индукция по числу вершин n . Для n 2 утверждение верно.
78
Пусть теорема выполняется для числа вершин 2 n k и |
T – дерево с (k 1) -й |
|||||||||||||
вершиной, а B0 – его усечѐнная матрица инцидентности. Дерево T |
имеет, по крайней ме- |
|||||||||||||
ре, две висячие вершины, и, по крайней мере, одна строка матрицы B0 соответствует этой |
||||||||||||||
вершине. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этой строке (обозначим еѐ i ) только один ненулевой элемент 1. Пусть вершина vi |
ин- |
|||||||||||||
цидентна l -му ребру. |
Матрицу, полученную из B0 |
вычѐркиванием i -й строки и |
j -го |
|||||||||||
столбца, обозначим B |
|
|
|
B |
|
. Поскольку |
B – усечѐнная матрица для дерева |
|||||||
. Тогда |
B |
|
|
|||||||||||
0 |
|
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
T , полученного из T |
удалением i -й вершины и l -го ребра, то |
|
B |
|
1 по предположе- |
|||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
нию индукции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
||
Следствие. Ранг матрицы инцидентности связного графа G на n вершинах равен |
||||||||||||||
(n 1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение 5. Пусть имеется связный граф G и его остов T . Перенумеруем сначала хорды, а потом ветви графа G . Каждому фундаментальному разрезу придадим ориентацию, совпадающую с ориентацией соответствующей ветви. Матрицу K (kij )
размера (n 1) m , строки которой соответствуют фундаментальным разрезам, а
столбцы – дугам орграфа G , будем называть матрицей фундаментальных разрезов, ес-
ли:
1,
kij 1,
0,
если j-я дуга принадлежит i-му разрезу и еѐ ориентация совпадает с ориентацией разреза; если j-я дуга принадлежит i-му разрезу и еѐ ориентация не совпадает с ориентацией разреза; если j-я дуга не принадлежит i-му разрезу.
Определение 6. Пусть имеется связный граф G и его остов
T . Перенумеруем сначала хорды, а потом ветви графа G . Каждому фундаментальному циклу придадим ориентацию, совпадающую с ориентацией соответствующей хорды.
Матрицу ( ij ) размера (m n 1) m , строки которой соответствуют фундамен-
тальным циклам, а столбцы – дугам орграфа G , будем называть матрицей фундамен-
тальных циклов, если:
1,
ij 1,
0,
если j-я дуга принадлежит i-му циклу и еѐ ориентация совпадает с ориентацией цикла; если j-я дуга принадлежит i-му циклу и еѐ ориентация не совпадает с ориентацией цикла; если j-я дуга не принадлежит i-му циклу.
79
Следующие три теоремы приведѐм без доказательства.
Теорема 2. Пусть G – связный граф, Е – его остов, B, K, – матрицы инци-
дентности, фундаментальных разрезов и фундаментальных циклов соответственно. То-
гда
B T 0, K T 0 .
Определение 7. Матрица X размера p q называется унимодулярной, если оп-
ределитель любой еѐ квадратной подматрицы равен 1, –1 или 0.
Теорема 3. Матрицы инцидентности, фундаментальных циклов и фундамен-
тальных разрезов связного графа G унимодулярны.
Теорема 4. Пусть G – связный граф, B0 – усечѐнная матрица инцидентности какой-либо из ориентаций графа G . Тогда число остовов графа G равно B0 B0T .
Задачи
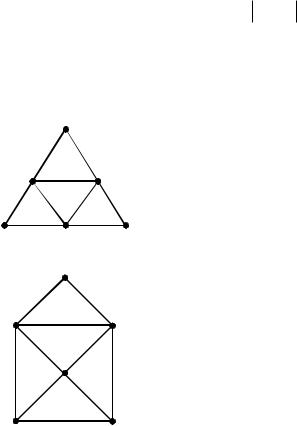
Найдите матрицу смежности графа G . С еѐ помощью найдите число маршрутов из
вершины v2 в вершину v5 длины 3.
1. |
v1 |
|
|
|
|
v2 |
|
v3 |
v4 |
v5 |
v6 |
2. |
v1 |
|
|
|
|
v2 |
|
v3 |
|
v4 |
|
v5 |
|
v6 |
Задайте некоторую ориентацию графа G . Для данного остова T перенумеруйте сначала ветви, а потом хорды графа. Найдите матрицы инцидентности B , фундаменталь-
ных циклов и разрезов K графа G . Проверьте, что B T 0 и K T 0 .
80
