ИФПМ (ПРИТ) / Учебник

ный многочлен для 2 ,... и т.д. Рассмотрим циклический код с порождающим многочле-

ном

g(x) НОК m1(x), m2 (x),..., md 1(x) .

Если n 2r 1, а k n deg g(x) , то получим (n, k) -код с минимальным расстоянием

Еѐ определитель есть произведение n1 n2 ... nd 1 на определитель Вандермон-

да. Поэтому 0 . Отсюда bi 0 .

Теорема доказана.

Определение 2. Код, описанный в теореме 1, называется БЧХ-кодом.

БЧХ-коды были введены Боузом и Чоудхури в 1959 г. и Хоквингемом в 1960 г. Они используются в течение многих лет в европейских и трансатлантических информацион-

ных системах связи. Сообщения в них имеют длину 231, а порождающий многочлен име-

ет степень 24, так что длина кодовых слов равна 231 + 24 = 255 =28 – 1. Этот код обнару-

живает, по меньшей мере, 6 ошибок, и вероятность неправильного декодирования – одна

16-миллионная.

51

Допустим, на приѐм поступила последовательность v (111110000000000) . Стоит задача исправить ошибки в этом слове. Тогда S1 1 2 3 4 3 2 .

Далее

S3 1 3 6 9 12 1 3 2 3 2 1 0 .

Если x1 и x2 – степени элемента , соответствующие номерам координат, в кото-

рых допущены ошибки (например, если ошибки допущены в 3-й и 10-й позициях, то

Поскольку x12 x22 (x1 x2 )2 ( 2 3 )2 3 2 1 , то x1x2 3 2 1.

Таким образом, x1 и x2 являются корнями квадратного уравнения x2 ( 3 2 )x 3 2 1 0 .

Подбором находим корни x1 , x2 11 . Значит, вектор v имеет ошибки во 2-й и в

12-й позициях. После исправления получаем вектор

u (101110000001000) .

Ещѐ один пример: v (1111110000000000) .

S1 1 2 3 4 5 1 2 3 1 2 3 .

Учитывая предыдущие вычисления, S3 1. Тогда S1 1 6 3 2 , S12 18 3 . По-

этому x1x2 2 . Но уравнение

x2 ( 3 )x 2 0

решений не имеет! Это говорит о том, что ближайшее кодовое слово отстоит от вектора v на расстоянии, бóльшем чем 2, и его нельзя декодировать.

53

многочлена кода возьмѐм

g(x) (x4 x 1)(x4 x3 x2 x 1) x8 x7 x6 x4 1.

Тогда k n deg g(x) 15 8 7 . Получим (15, 7) -код с минимальным расстоянием 5,

исправляющий 2 ошибки. Допустим, что на приѐм получено слово u , в котором не более двух ошибок. Исправьте их.

54

3.Графы

3.1.Введение в графы. Задача о кѐнигсбергских мостах.

Проблема четырѐх красок

Начало теории графов относится к 1736 году, когда Леонард Эйлер (1707 – 1783) не только решил популярную в то время задачу о кѐнигсбергских мостах, но и нашѐл крите-

рий существования в графе специального маршрута (эйлерова цикла, как теперь его назы-

вают). Однако этот результат более ста лет оставался единственным результатом теории графов. Лишь в середине XIX века инженер-электрик Густав Кирхгоф (1824 – 1895) раз-

работал теорию деревьев для исследования электрических цепей, а математик Артур Кэли

(1821 – 1895) в связи с описанием строения углеводородов решил перечисленные задачи для трѐх типов деревьев. К этому же периоду относится появление знаменитой проблемы четырѐх красок.

Остановимся подробнее на задаче о кѐнигсбергских мостах. Суть еѐ в следующем.

В г. Кѐнигсберге посередине реки были два острова. Эти острова соединялись между

собой и с обоими берегами реки системой мостов. Если каждый отделѐнный участок суши обозначить точкой, а каждый мост изобразить «ребром», то получится следующая схема:

Точку (вершину) назовѐм чѐтной, если из неѐ выходит чѐтное число рѐбер, и нечѐт-

ной в противном случае. Решение Эйлера состояло в следующем. «Граф» можно обойти,

если число нечѐтных вершин равно 0 или 2. В данном случае все четыре вершины являют-

ся нечѐтными, поэтому обойти все мосты, побывав на каждом ровно один раз, нельзя.

Многие, наверное, знакомы со следующей «детской» задачей. Можно ли

55

нарисовать домик, не отрывая ручки от бумаги? В данном случае ответ положительный,

так как число нечѐтных вершин равно 2. Только начинать и заканчивать обход нужно обя-

зательно в вершине нечѐтной степени:

Другой очень известной задачей теории графов является проблема четырѐх красок.

Суть еѐ состоит в следующем. На плоскости имеется географическая карта, на которой нанесены страны со своими границами. Всегда ли хватит четырѐх красок, чтобы раскра-

сить эту карту таким образом, чтобы любые две граничащие страны были раскрашены в разные цвета? Каждая страна, естественно, окрашивается в один цвет. То, что число кра-

сок должно быть не меньше четырѐх, показывает, например, следующая карта:

Эта проблема стояла около 100 лет и была окончательно разрешена относительно недавно (в 1976 году) американскими математиками Хакеном и Аппелем при использова-

нии вычислительной техники.

1

3 4

2

3.2. Графы. Основные понятия

Определение 1. Пусть V – некоторое множество, называемое в дальнейшем множеством вершин, V2 – множество всех его двухэлементных подмножеств. Пусть

E V2 – некоторое подмножество в V2 , называемое в дальнейшем множеством рѐбер.

Тогда пара (V , E) называется простым графом или просто графом. Эта пара часто обо-

значается G(V , E) или просто G .

Если e E, e (v1,v2 ) , то вершины v1,v2 будем называть концами ребра e . Будем также говорить, что вершины v1,v2 инцидентны ребру e или ребро e инцидентно вер-

шинам v1 и v2 . Вершины, соединѐнные ребром, будем называть соседними, а рѐбра, инци-

дентные одной и той же вершине, смежными.

В некоторых случаях рассматривают графы, в которых две фиксированные верши-

ны могут быть соединены не одним ребром, а несколькими. Могут также рассматриваться графы с «петлями», т.е. с рѐбрами вида (v,v) . Такие графы пока рассматривать не будем.

Будем рассматривать только конечные графы, т.е. множество вершин V всегда предполагается конечным.

56

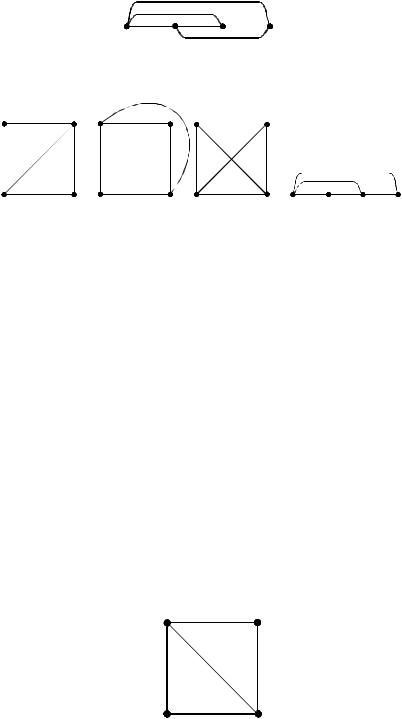
Пример 1. Рассмотрим граф G(V , E) , где

E {(a,b), (a,c), (a,d ), (b,c), (b,d )}. Его можно изобразить с помощью следующего рисунка:

Однако его можно изобразить и по-другому:

Разные рисунки представляют один и тот же граф. В связи с этим важным является понятие изоморфизма графов.

Определение 2. Графы G1(V1, E1) и G2 (V2 , E2 ) называются изоморфными, если существует такое взаимно однозначное отображение

f :V1 V2 ,

что любые две вершины соединены ребром в графе G1 тогда и только тогда, ко-

гда их образы соединены ребром в графе G2 , т.е.

(a,b) E1 ( f (a), f (b)) E2 .

Теперь несложно убедиться, что все нарисованные выше графы изоморфны.

Важной характеристикой графа является группа его автоморфизмов. Она отражает меры симметрии этого графа.

Определение 3. Пусть имеется граф G . Изоморфизмы графа G в себя называ-

ются автоморфизмами. Все автоморфизмы графа G образуют группу, которая называ

ется группой автоморфизмов графа G и обозначается .

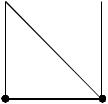
Пример 2. Найдѐм группу автоморфизмов следующего графа:

Можно произвольным образом перенумеровать вершины графа и среди всех пере-

становок вершин выбрать те, которые удовлетворяют определению изоморфизма графов.

Перенумеруем вершины таким образом:

57

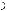
2 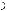3

Тогда автоморфизмами графа будут следующие перестановки:

Как известно, существуют две группы из четырѐх элементов и обе они абелевы.

Это 4 и 2 2 . Поскольку порядки получившихся автоморфизмов не более 2, то

Aut G 2 2 .

Определение 4. Маршрутом в графе G(V , E) называется последовательность

вершин и рѐбер v1, (v1,v2 ), v2 , (v2 ,v3 ),..., (vk 1,vk ), vk , начинающаяся и заканчивающаяся вершиной.

Маршрут, в котором все рѐбра разные, называется цепью. Цепь, в которой все

вершины разные, называется простой цепью.

Определение 5. Цепь, в которой первая и последняя вершины совпадают, назы-

вается циклом. Цикл, в котором все вершины, кроме первой и последней, разные, называ-

Определение 7. Граф G называется связным, если каждая пара его вершин со-

единена цепью.

Определение 8. Пусть G(V , E) – произвольный граф. Тогда множество его вер-

шин V можно разбить на такие непересекающиеся подмножества V1,V2 ,...,Vp , что лю-

бые две вершины из Vi (i 1,..., p) соединены цепью и никакая вершина из Vi не соединена цепью ни с какой вершиной из V j при i j .

Пусть Ei обозначает множество всех рѐбер из E , оба конца которых принадле-

жат Vi . Тогда подграфы G1(V1, E1), G2 (V2 , E2 ),..., Gp (Vp , Ep ) называются компонентами связности графа G .

58

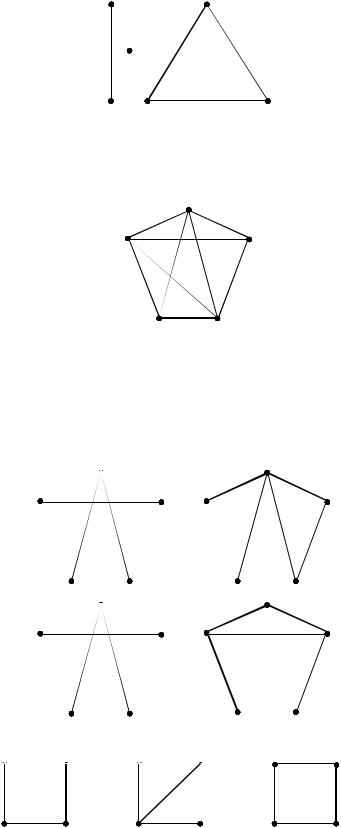
Пример 3. Граф, изображѐнный на рисунке, имеет 3 компоненты связности:

Определение 9. Граф G называется полным, если любые его две вершины со-

единены ребром. Полный граф на n вершинах обозначается Kn .

Пример 4. Граф K5 :

Задачи

Изоморфны ли следующие графы?

1. 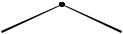и

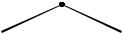2. и

Для следующих графов найдите их группы автоморфизмов.

3. 4. 5.

6.Найдите все неизоморфные графы с четырьмя вершинами.

7.Найдите все с точностью до изоморфизма (5,5) -графы.

59

3.3. Деревья

Определение 1. Деревом называется связный граф без циклов.

В дальнейшем договоримся (n, m) -графом называть граф, в котором n вершин и

m рѐбер.

Теорема. Пусть G(V , E) – (n, m) -граф. Тогда следующие условия эквивалентны:

1)G – дерево;

2)G – связный граф и m n 1;

3)G – граф без циклов и m n 1.

Доказательство. 1 2. Индукция по n . При n 1 граф состоит только из одной

вершины и утверждение верно. Предположим, что утверждение справедливо, когда число вершин меньше n . Рассмотрим случай V n .

Пусть ребро e E . Удалим ребро e из графа G . Получим граф G V , E \{e} . Если

v1,v2 – концевые вершины ребра e , то в графе G вершины v1 и v2 не могут быть соеди-

нены цепью, так как иначе в графе G был бы цикл. Значит, число компонент связности

ненте связности, что и v1 . Если же цепь содержит ребро e , то данная вершина в графе G

соединена с v2 и, таким образом, число компонент связности графа G равно в точности двум. Пусть G1(V1, E1), G2 (V2 , E2 ) – это компоненты связности,

ченный граф G1 по-прежнему останется связным. Если G1 также содержит цикл, то опять удалим ребро, входящее в цикл. После повторения этой процедуры, например, p раз по-

лучим связный граф без циклов, т.е. дерево. В силу того что импликация 1 2 уже дока-

зана, можем утверждать, что m p n 1. Это противоречит условию, поскольку p 0 .

3 1. Допустим, что граф G не является связным. Тогда он распадается на k ком-

понент связности G1,...,Gk , k 1. В этом случае каждая компонента связности Gi (Vi , Ei ) яв-

60