
ИФПМ (ПРИТ) / Учебник
.pdfляется деревом. Пусть |
|
Vi |
|
ni , |
|
Ei |
|
mi . Тогда по доказанному (1 2) |
mi ni 1 . Суммируя |
|
|
|
|
|
|||||||
эти равенства по i , получаем |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
k |
k |
|
|
|
|
|
|
|
|
|
m mi ni k n k , |
|
|
|
|
|
|
|
|
|
|
i 1 |
i 1 |
|
что противоречит условию, так как k 1.
Теорема доказана.
Определение 2. Число рѐбер, которым инцидентна вершина v , будем называть степенью вершины v и обозначать d (v) .
В случае d (v) 1 вершину v будем называть висячей.
Следствие. В любом дереве на n вершинах при n 2 имеется не менее двух висячих вершин.
n
Доказательство. Пусть v1,..., vn – все вершины графа G . Тогда d (vi ) равна уд-
i 1
военному числу рѐбер, так как каждое ребро графа, инцидентное вершинам vi ,v j , увели-
чивает их степень на 1. Поскольку m n 1, то d(vi ) 2m 2n 2 . Но если бы d (vi ) 2n ,
то d (vi ) 2n . Значит, как минимум, две вершины являются висячими.
Задачи
1.Найдите все с точностью до изоморфизма деревья с 5-ю вершинами.
2.Найдите все с точностью до изоморфизма деревья с 6-ю вершинами.
3.Найдите все с точностью до изоморфизма деревья с 7-ю вершинами.
4.Найдите наименьшее n 2 , для которого существует дерево с n вершинами,
имеющее единичную группу автоморфизмов.
5. Степенной последовательностью графа называется последовательность степеней его вершин, расположенная в порядке убывания. Найдите два неизоморфных дерева с одинаковой степенной последовательностью.
61
3.4. Помеченные графы. Код Прюфера
Определение 1. Граф G(V , E) будем называть помеченным, если каждой верши-
не присвоена своя метка. Обычно полагают V 1, 2,..., n . Два помеченных графа G1(V1, E1)
и G2 (V2 , E2 ) |
считаются одинаковыми в точности тогда и только тогда, |
когда V1 V2 и |
|||||||||||
E1 E2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
1 |
4 |
1 |
3 |
2 |
3 |
3 |
|
2 |
|
|
|
3 |
2 |
2 |
3 |
2 |
4 |
1 |
4 |
1 |
|
4 |
|
|
|
Пример 1. Следующие помеченные графы являются разными: |
|
|
||||||||||
|
Следующие помеченные графы одинаковые: |
|
|
|
|
|
|
||||||
|
Предложение 1. Число помеченных (n, m) |
-графов равно |
Cm 2 |
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
(Cn ) |
|
|
|
|
|
|
1 |
|
4 |
2 |
|
3 |
|
|
|
|
|
|
|
|
3 |
|
2 |
4 |
|
1 |
|
|
|
|
|
|
Доказательство. Существует C 2 |
неупорядоченных пар вершин, которые можно |
|||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
соединить ребром. Если нужно выбрать k |
рѐбер, то это можно сделать Ck 2 |
|
способами. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
(C p ) |
|
|
|
Предложение доказано. |
|
|
|
|
|
|
|
|
|
|
||
|
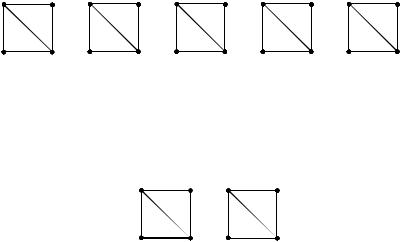
Например, число помеченных графов с 4-мя вершинами и 5-ю рѐбрами равно |
||||||||||||
C5 2 |
C5 6 |
. Все они изображены в начале этого параграфа. |
|
|
|
|
|
||||||
(C4 ) |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
. |
|
Предложение 2. Число помеченных графов на n вершинах равно 2 n |
||||||||||||
Доказательство. Множество рѐбер каждого помеченного графа на n вершинах есть некоторое подмножество в множестве всевозможных рѐбер, число которых, как было
сказано выше, равно Cn2 . Число таких подмножеств есть Предложение доказано.
62
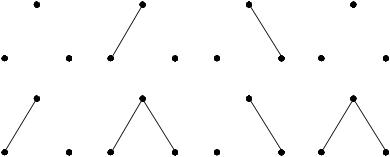
Пример 2. Число помеченных графов на 3-х вершинах равно 2C32 23 8 . Вот они
2 |
|
2 |
|
2 |
|
|
2 |
|
||
1 |
|
3 |
1 |
3 |
1 |
|
3 |
1 |
|
3 |
2 |
|
2 |
|
2 |
|
|
2 |
|
||
1 |
|
3 |
1 |
3 |
1 |
|
3 |
1 |
|
3 |
Поясним, что помеченное дерево – это помеченный граф, являющийся деревом.
Теорема (Кэли). Число помеченных деревьев на n вершинах равно nn 2 .
Доказательство этой теоремы может быть основано на следующем алгоритме, со-
поставляющем каждому дереву некоторую последовательность номеров его вершин, ко-
торая называется кодом Прюфера этого дерева. Опишем этот алгоритм.
Пусть имеется помеченное дерево T на n вершинах. Как минимум, две его верши-
ны являются висячими. Пусть b1 – висячая вершина с наименьшим номером, а e1 (b1, a1)
– соответствующее висячее ребро. Удалив из дерева T ребро e1 и вершину b1 , получим новое дерево T1 . Для T1 опять найдѐм висячую вершину b2 с наименьшим номером. Соот-
ветствующее висячее ребро обозначим e2 (b2 , a2 ) и т.д. Продолжим эту процедуру до тех пор, пока не останется единственное ребро en 1 (bn 1, an 1) . Набор a1, a2 ,..., an 2 и будет кодом Прюфера дерева T .
Каждый код Прюфера, т.е. любой набор из (n 2) чисел, каждое из которых может принимать значения от 1 до n , однозначно соответствует своему дереву. В этом можно убедиться с помощью следующей обратной процедуры.
Действительно, пусть имеется код a1, a2 ,..., an 2 . Запишем последовательность на-
туральных чисел от 1 до n : 1, 2,3,...,n . Среди этих чисел находим наименьшее число, не содержащееся в коде. Пусть это будет b1 . Рисуем ребро e1 (b1, a1) . Число a1 удаляем из кода, а число b1 удаляем из набора 1, 2,3,..., n . Далее в наборе 1, 2,3,..., n \{b1} находим наименьшее число, не содержащееся в оставшейся части кода a2 ,..., an 2 . Пусть это будет b2 . Изображаем ребро e2 (b2 , a2 ) . Далее рассматриваем часть кода a3 ,..., an 2 и набор
1, 2,3,..., n \{b1,b2} . Продолжим эту процедуру до тех пор, пока в наборе 1, 2,3,..., n не ос-
танутся лишь две вершины v1 и v2 . Соединив их ребром, получим дерево на n вершинах.
63
Можно показать, что указанное соответствие между помеченными деревьями на n
вершинах и всевозможными кодами Прюфера, состоящими из n 2 чисел, является вза-
имно однозначным.
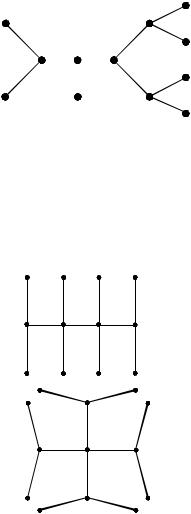
Пример 3. Дерево
|
|
|
|
|
7 |
8 |
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
3 |
4 |
|
6 |
9 |
|||
|
|
||||||
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
2 |
|
|
|
5 |
11 |
12 |
|
|
|
|
|||||
|
|
|
|
||||
|
|
|
|
|
|||
имеет код 3,3, 4, 4,6,7,7,6,11,11 .
Задачи
Перенумеруйте вершины дерева и найдите его код Прюфера.
1.
2.
По заданному коду Прюфера восстановите помеченное дерево.
3.5,5,5,1, 2,3,12,12,11,11 .
4.9,8,7,6,5,6,7,8,9,10 .
3.5. Алгоритм Краскала
На языке помеченных графов формулируются многие виды прикладных задач. В
данном и следующем параграфах рассмотрим две из них.
Допустим, нужно построить сеть железных дорог, которые соединили бы n данных городов так, чтобы из каждого города можно было бы приехать в любой другой город.
Пусть для каждой пары городов известна стоимость строительства дороги между ними.
64
Как построить дерево, соединяющее эти n городов, чтобы общая стоимость строительства была минимальной?
Алгоритм решения данной задачи известен под названием алгоритма Краскала.
Определение 1. Граф G(V , E) называется взвешенным, если каждому его ребру e присвоено некоторое действительное число (e) , называемое его весом. Другими сло-
вами, задана функция f : E . Если задан подграф G (V , E ) графа G , то его весом на-
зывается (G ) (e) .
e G
Определение 2. Пусть имеется связный граф G . Связный подграф G графа G ,
содержащий все вершины графа G и являющийся деревом, называется остовом графа G .
Связный граф может иметь много остовов.
Таким образом, задача о соединении городов сводится к нахождению остова наи-
меньшего веса.
Теорема. Пусть G – связный граф на вершинах. Тогда следующая процедура при-
водит к решению задачи о соединении городов:
(i)выберем ребро e1 , обладающее в G наименьшим весом;
(ii)определим по индукции последовательность рѐбер e2 ,e3,...,en 1 , выбирая на
каждом шаге ребро, отличное от предыдущих, не образующее циклов с множеством предыдущих рѐбер и обладающее среди таких ребер наименьшим весом.
Полученный подграф T графа G , ребрами которого являются e1,...,en 1 , и есть требуемое дерево.
Доказательство. Поскольку T без циклов и m n 1, то T – дерево, что следует из теоремы 1 § 3.2. Покажем, что сумма весом рѐбер дерева T минимальна.
Допустим противное, т.е. что существует дерево S , для которого (S) (T ) . Пусть
– рѐбра дерева T , принадлежащие также и S , а ek – первое ребро из T , не при-
надлежащее S . Подграф графа G , полученный присоединением ребра ek к S , даѐт единст-
венный цикл C . Так как ek T , то цикл C содержит ребро, не принадлежащее T . Обозна-
чим его e |
. Подграф, полученный из |
S |
заменой e |
на e , |
по-прежнему является деревом |
k |
|
|
k |
k |
|
(как связный граф, в котором m n 1), |
причѐм (S ) (S) |
и S и T имеют общие рѐбра |
|||
e1,..., ek . Продолжая этот процесс, преобразуем S в T . Но тогда (T ) (S) (T ) . Противо-
речие.
Теорема доказана.
65
Пример. Пусть имеется следующая матрица стоимостей строительства дорог:
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
|
13 |
14 |
12 |
15 |
16 |
2 |
|
|
9 |
7 |
5 |
6 |
3 |
|
|
|
8 |
11 |
10 |
4 |
|
|
|
|
1 |
2 |
5 |
|
|
|
|
|
2 |
6 |
|
|
|
|
|
|
Требуется найти остов наименьшего веса.
Сначала выбираем ребро e1 (4,5) наименьшего веса 1. Далее берѐм ребро e2 (4,6)
наименьшего веса 2. Следующим ребром наименьшего веса является ребро (5,6) . Но оно образует цикл с предыдущими двумя рѐбрами. Поэтому его пропускаем и берѐм следую-
щее ребро наименьшего веса e3 (2,5) . Рѐбра (2,6) и (2, 4) образуют циклы с предыдущи-
ми рѐбрами. Их пропускаем и берѐм ребро e4 (3, 4) . Рѐбра (2,3) , (3,6) и (3,5) взять нельзя,
поэтому следующим ребром, удовлетворяющим условиям алгоритма, будет ребро
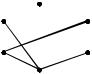
e5 (1, 4) . Рѐбра e1,e2 ,e3,e4 ,e5 образуют остов наименьшего веса 28. Соответствующий план дорог изображѐн ниже:
|
1 |
6 |
2 |
5 |
3 |
|
|
|
4 |
Задачи
Решите задачу о соединении городов с помощью алгоритма Краскала, если дана следующая матрица стоимостей строительства дорог.
1.
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
|
12 |
5 |
4 |
7 |
6 |
2 |
|
|
11 |
13 |
14 |
15 |
3 |
|
|
|
2 |
8 |
3 |
4 |
|
|
|
|
9 |
2 |
5 |
|
|
|
|
|
10 |
6 |
|
|
|
|
|
|
66
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
10 |
|
3 |
|
|
6 |
|
|
3 |
|
|
7 |
|
|
|||||||
2 |
|
|
|
|
|
|
10 |
|
|
9 |
|
|
10 |
|
|
10 |
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
3 |
|
|
7 |
|
|
||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
7 |
|
|
||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
4 |
|
5 |
|
|
6 |
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
6 |
|
7 |
|
9 |
|
8 |
|
|
7 |
|
|
|||||||||
2 |
|
|
|
|
|
|
|
8 |
|
7 |
|
9 |
|
|
6 |
|
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
3 |
|
|
7 |
|
|
|||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
4 |
|
|
||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
3 |
|
|
|
|
|
|
6 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
5 |
|
|
|
|
||||||
1 |
|
|
|
1 |
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
|||||||
2 |
|
|
|
|
|
|
6 |
|
|
7 |
|
|
1 |
|
|
2 |
|
|
||||||
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
|
5 |
|
|
|||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
7 |
|
|
|||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3.6. Метод ветвей и границ
Метод ветвей и границ применяется для решения следующей задачи. Имеется n
пунктов. Нужно обойти все пункты и вернуться в исходный пункт. Для каждой пары пунктов А и В имеется «стоимость» пути из А в В. Требуется найти простой цикл, прохо-
дящий через все пункты с наименьшей суммарной стоимостью. Очевидно, не имеет зна-
чения, из какого пункта начинать маршрут. Эту задачу часто называют задачей комми-
вояжѐра.
Определение 1. Простой цикл, проходящий через все вершины графа, называет-
ся гамильтоновым контуром.
Предложение 1. Число всех гамильтоновых контуров в полном графе на нах равно (n 1)! .
Доказательство. Будем считать, что вершины графа перенумерованы натураль-
ными числами от 1 до n . Можно считать, что гамильтонов контур начинается с первой
67
вершины. Остальные n 1 вершины можно переставлять произвольным образом. Число перестановок n 1 символа равно (n 1)! .
Предложение доказано.
Метод ветвей и границ во многих случаях позволяет сократить полный перебор всех
вариантов при решении задачи коммивояжѐра. Суть этого метода рассмотрим на следую-
щем примере.
Пусть дана следующая матрица стоимостей: |
|
|
|
|||||||
|
|
|
2 |
|
3 |
|
4 |
|
5 |
|
|
|
1 |
|
|
|
|
||||
1 |
|
30 |
|
40 |
|
15 |
|
6 |
|
|
2 |
10 |
|
|
18 |
|
7 |
|
9 |
|
|
3 |
20 |
30 |
|
|
|
0 |
|
10 |
|
|
4 |
25 |
10 |
|
35 |
|
|
|
5 |
|
|
|
5 |
9 |
8 |
|
7 |
|
6 |
|
|
|
Элемент aij этой матрицы равен стоимости переезда из пункта i в пункт j . Мат-
рица не обязательно должна быть симметричной. Например, если пункты i и j соединяет улица с односторонним движением, а роль стоимости переезда играет время, то элементы
aij и a ji будут разными.
Итак, опишем алгоритм решения задачи. Из каждой строки данной матрицы вы-
чтем минимальный элемент: |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
4 |
|
5 |
|
|
|
1 |
|
|
|
|
||||
1 |
|
24 |
|
34 |
|
9 |
|
0 |
|
|
2 |
3 |
|
|
11 |
|
0 |
|
2 |
|
|
3 |
20 |
30 |
|
|
|
0 |
|
10 |
|
|
4 |
20 |
5 |
|
30 |
|
|
|
0 |
|
|
|
5 |
3 |
2 |
|
1 |
|
0 |
|
|
|
Сумма элементов, которые вычли, равна h1 6 7 0 5 6 24 . Поскольку в каждом контуре имеется ребро с началом в каждой из вершин, то стоимость каждого из возмож-
ных маршрутов уменьшилась на одну и ту же величину 24, и поэтому оптимальный мар-
шрут для этих двух матриц будет одним и тем же.
Теперь совершим операцию аналогичную для столбцов матрицы:
|
1 |
2 |
|
3 |
4 |
5 |
1 |
|
22 |
|
33 |
9 |
0 |
2 |
0 |
|
|
10 |
0 |
2 |
3 |
17 |
28 |
|
|
0 |
10 |
4 |
17 |
3 |
|
29 |
|
0 |
5 |
0 |
0 |
|
0 |
0 |
|
|
|
|
68 |
|
|
|
Сумма элементов, которые вычли, равна h2 6 . Величина h h1 h2 30 называется константой приведения. В результате этих двух операций стоимость каждого маршрута уменьшилась на 30, и поэтому оптимальный маршрут останется неизменным.
Далее вычислим элементы матрицы, равные нулю:
(1;5), (2;1), (2;4), (3;4), (4;5), (5;1), (5;2), (5;3), (5;4) .
Для каждого такого элемента найдѐм сумму наименьших элементов в данной стро-
ке и столбце, за исключением самого этого элемента (который равен 0). Получим сле-
дующие значения: 9, 0, 0, 10, 3, 0, 3, 10, 0. Среди этих чисел выбираем наибольшее. Это
наибольшее равно 10 и соответствует рѐбрам (3;4) и (5;3) . Выберем первое из них и разо-
бьѐм множество всех маршрутов на 2 группы: первая группа А – это те из них, которые не содержат ребро (3;4) , а вторая В – те, которые содержат. Суммарная стоимость маршрутов группы А не менее 40. Поэтому оптимальный маршрут имеет смысл искать среди маршру-
тов группы В. Из матрицы вычеркнем 3-ю строку и 4-й столбец. Элемент (4;3) при этом заменяем на , так как гамильтонов контур не может содержать двух одинаковых рѐбер:
|
1 |
2 |
3 |
5 |
1 |
|
22 |
33 |
0 |
2 |
0 |
|
10 |
2 |
4 |
17 |
3 |
|
0 |
5 |
0 |
0 |
0 |
|
Так как в каждой строке и каждом столбце есть 0, то константа приведения равна 0.
Опять выписываем элементы, равные 0 и соответствующие им числа:
(1;5), |
(2;1), |
(4;5), |
(5;1), |
(5;2), |
(5;3) |
22 |
2 |
3 |
0 |
3 |
10 |
Производим ветвление по ребру 1;5 . Маршруты группы В делим на две группы:
группа ВА – маршруты, не содержащие ребро (1;5) (их стоимость не менее 30 + 22 = 52), и
маршруты группы ВВ, содержащие ребро 1;5 . Из матрицы вычѐркиваем 1-ю строку и 5-й
столбец. Элемент 5;1 заменяем на : |
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
3 |
|
|
|
|
1 |
|
|
|
||
2 |
0 |
|
|
|
10 |
|
||
4 |
17 |
|
3 |
|
|
|
||
|
5 |
|
|
0 |
|
0 |
|
|
После приведения получим матрицу |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
1 |
|
2 |
|
3 |
|
2 |
0 |
|
|
|
10 |
|
||
4 |
14 |
|
0 |
|
|
|
||
5 |
|
|
0 |
|
0 |
|
||
|
|
|
|
69 |
|
|
|
|
Маршруты группы ВВ имеют стоимость не менее 33. Выписываем рѐбра, соответ-
ствующие нулям, и их числа
(2;1), |
(4; 2), |
(5; 2), |
(5;3) |
24 |
14 |
0 |
10 |
Производим ветвление по ребру 2;1 . К группе ВВА относим маршруты, не содер-
жащие рѐбра 2;1 . Их стоимость не менее 33 24 57 . К маршрутам группы ВВВ отнесѐм
те, которые содержат ребро 2;1 . Стягиваем матрицу
|
2 |
3 |
4 |
0 |
|
5 |
0 |
0 |
Осталось взять ребро 4; 2 и 5;3 . Получили гамильтонов контур
1 5 3 4 2 1.
Его стоимость равна 33. Так как минимальные стоимости маршрутов групп А, ВА,
ВВА больше, то этот маршрут будет оптимальным.
Задачи
Методом ветвей и границ решите задачу коммивояжѐра со следующей матрицей.
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
4 |
|
|
|
|
|
|
|
5 |
||||
1 |
|
|
3 |
|
4 |
|
5 |
6 |
||
2 |
2 |
|
|
|
3 |
|
4 |
5 |
||
3 |
6 |
|
3 |
|
|
|
6 |
3 |
||
4 |
4 |
|
5 |
|
6 |
|
|
4 |
||
5 |
3 |
|
4 |
|
5 |
|
6 |
|
||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
2 |
|
3 |
|
4 |
5 |
1 |
|
|
3 |
|
4 |
|
5 |
3 |
||
2 |
4 |
|
|
|
4 |
|
5 |
3 |
||
3 |
5 |
|
3 |
|
|
|
4 |
5 |
||
4 |
4 |
|
5 |
|
3 |
|
|
3 |
||
|
5 |
4 |
|
5 |
|
3 |
|
4 |
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
4 |
|
5 |
|
|
|
1 |
|
|
|
|
||||
1 |
|
30 |
|
46 |
|
19 |
|
2 |
|
|
2 |
10 |
|
|
19 |
|
3 |
|
2 |
|
|
3 |
21 |
15 |
|
|
|
35 |
|
0 |
|
|
4 |
26 |
22 |
|
30 |
|
|
|
4 |
|
|
5 |
3 |
4 |
|
3 |
|
2 |
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
