
ИФПМ (ПРИТ) / Учебник
.pdf
3.
v2

v4
4.
v2

v4
5.
v2

v5

6.
v2

v5

v1 |
|
|
|
|
v1 |
|
|
|
v3 |
|
|
v2 |
|
v3 |
|
v5 |
v6 |
v4 |
v5 |
|
v6 |
||
G |
|
|
|
|
T |
|
|
v1 |
|
|
|
|
v1 |
|
|
|
v3 |
|
|
v2 |
|
v3 |
|
v5 |
v6 |
v4 |
v5 |
|
v6 |
||
G |
|
|
|
|
T |
|
|
v1 |
|
|
|
|
v1 |
|
|
v4 |
v3 |
v2 |
|
|
v4 |
|
v3 |
|
|
|
|
|
|
||
G |
v6 |
v5 |
|
|
T |
|
v6 |
|
|
||||||
|
|
|
|
|
|
||
v1 |
|
|
|
|
v1 |
|
|
|
v3 |
v2 |
|
|
v3 |
||
v4 |
|
|
|
|
v4 |
|
|
G |
v6 |
v5 |
T |
|
v6 |
||
|
|
|
|
|
|
||
Даны матрица смежности B графа G и ветви его остова T . Найдите матрицы фун-
даментальных циклов, разрезов и смежности. Изобразите граф G .
|
0 |
0 |
0 |
0 |
0 |
1 |
1 0 |
||
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
|||||||||
|
0 |
1 |
0 |
0 |
0 |
0 |
|
1 1 |
|
B |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
|
|
||||||||
|
1 0 |
1 1 0 |
0 |
0 |
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
|
|
||||||||
7. Ветви: a5 , a6 , a7 , a8 , a9 . 8. Ветви: a1, a3, a4 , a6 , a9 .
Пусть 1, 2 ,..., k – все фундаментальные циклы графа го остова T . Изобразите граф G и остов T .
0
0
1 .
0
1 0
G относительно некоторо-
81

9.1 a1, a6 , a7 , a9 , 2 a2 , a6 , a7 , 3 a3, a7 , a9 , 4 a4 , a5 , a6 , a7 , a9 .
10.1 a1, a4 , a5 , 2 a2 , a3, a3, a5 , a8 , 3 a3, a4 , a5 , a6 , a7 , a8 , 4 a3, a8 , a9 .
Найдите число остовов графа G по формуле и нарисуйте эти остовы:
11.



12.
3.10.Планарные графы
Определение 1. Говорят, что граф G укладывается на поверхности S , если его можно нарисовать на этой поверхности таким образом, что его рѐбра не будут пересе-
каться во внутренних точках.
Граф называется планарным, если его можно уложить на плоскости. Планарный
граф, изображѐнный на плоскости, называется плоской укладкой этого графа.
Определение 2. Гранью плоской укладки графа G будем называть наибольшее по включению множество на плоскости, две любые точки которого можно соединить непрерывной кривой, не пересекающейся с рѐбрами этой укладки. Границей грани будем считать множество вершин и рѐбер, принадлежащих этой грани. Точки границы грани будем считать принадлежащими данной грани. Грань будем называть конечной, если еѐ
площадь конечна, и бесконечной в противном случае.
Определение 3. Пусть f1, f2 ,..., fr – грани плоской укладки графа G , причѐм fr –
бесконечная грань. Обозначим через C1 (1 i r 1) цикл на границе грани fi .
Теорема 1. Циклы C1,C2 ,...,Cr 1 образуют базис пространства циклов.
Доказательство. Заметим, что сумма циклов
Ci1 ... Cim
содержит внутри себя грани fi1 ,..., fim . Внутренние точки других граней эта сумма циклов содержать не может. Поэтому никакой цикл Ci нельзя выразить через остальные.
Каждый элемент пространства циклов является циклом (возможно пустым), или объеди-
нением рѐберно непересекающихся циклов. Пусть цикл C содержит внутри себя конеч-
ную область, являющуюся объединением граней |
fi |
,..., fi |
. Тогда C Ci |
... Ci . |
|
1 |
m |
1 |
m |
82 |
|
|
|
|
Теорема доказана.
Теорема 2 (Эйлер). Если связный планарный граф имеет m рѐбер, n вершин и r
граней, то n m r 2 .
Доказательство. Поскольку размерность пространства циклов равна
(§ 3.8, теорема 3), то m n 1 r 1 , откуда n m r 2 .
Ввиду важности этого утверждения приведѐм ещѐ одно доказательство.
Для дерева формула верна, поскольку m n 1, r 1. Если связный граф не является
деревом, то он содержит циклы. Будем удалять рѐбра, принадлежащие циклам, до тех пор,
пока граф не превратится в дерево. Тогда формула будет верна. Далее будем
возвращать по одному ребру. При этом m и r будут увеличиваться на 1, а n меняться не будет. Следовательно, после возвращения всех рѐбер формула останется верной.
Теорема доказана.
Определение 4. Ребро e графа G называется мостом, если удаление этого ребра из графа увеличивает число компонент связности графа.
Определение 5. Степенью d ( f ) грани f некоторой укладки планарного графа
G называется число рѐбер на границе этой области, причѐм мосты считаются дважды.
Теорема 3. Если связный планарный граф G имеет m рѐбер и n 3 вершин, то
m 3n 6 .
Доказательство. Если n 3 , то степень любой грани не может быть меньше 3. По-
скольку каждое ребро графа даѐт вклад в сумму степеней его граней равный 2, то
d ( f ) 2m 3r . Отсюда |
r |
2 |
m . Тогда |
2 n m r n m |
2 |
m n |
1 |
m . Следовательно, |
|
|
|
|
|||||||
|
3 |
|
3 |
|
3 |
||||
6 3n m , т.е. m 3n 6 . |
|
|
|
|
|
|
|
|
|
Теорема доказана. |
|
|
|
|
|
|
|
|
|
Следствие. Граф K5 непланарен. |
|
|
|
|
|
|
|||
Доказательство. |
Действительно, |
для K5 n 5, m 10, 3n 6 9 , что противоречит |
|||||||
доказанному неравенству. |
|
|
|
|
|
|
|||
Следствие доказано. |
|
|
|
|
|
|
|||
Определение 6. |
Граф G(V , E) |
называется двудольным, |
если множество его |
||||||
вершин V можно разбить на такие два непересекающихся подмножества V1 и V2 , что один конец любого ребра из E принадлежит V1 , а другой – V2 .
Если множество вершин графа разбито на два непересекающихся подмножества
V1 и V2 и каждая вершина из V1 соединена ребром с каждой вершиной из V2 , то такой
83
граф называется полным двудольным графом, если |
|
V1 |
|
s, |
|
V2 |
|
t , то полный двудольный |
|
|
|
|
|||||
граф обозначается Ks,t . |
|
|
||||||
Теорема 4. Если связный двудольный планарный граф G имеет m рѐбер и n 3
.
Доказательство. Поскольку граница любой грани планарного графа при n 3 яв-
ляется циклом, а любой |
цикл |
в двудольном |
графе имеет |
длину |
не менее 4, то |
|||||||
d ( f ) 2m 4r . Отсюда |
r |
1 |
m . |
Тогда |
2 n m r n m |
1 |
m n |
1 |
m . Следовательно, |
|||
|
|
|
||||||||||
|
2 |
|
|
|
2 |
|
2 |
|
|
|||
4 2n m , т.е. m 2n 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
Следствие. Граф K3,3 непланарен. |
|
|
|
|
|
|
|
|
||||
Доказательство. Действительно, |
для K3,3 |
n 6, m 9, 2n 4 8 , |
что противоречит |
|||||||||
доказанному неравенству.
Следствие доказано.
Определение 7. Два ребра, инцидентные вершине степени 2, называются после-
довательными рѐбрами.
Пусть e1 (u,v) и e2 (v, w) – последовательные рѐбра, инцидентные вершине v .
Удаление вершины v и замена рѐбер e1 и e2 ребром (u, w) называется слиянием последо-
вательности.
Добавление новой вершины v на ребро (u, w) посредством введения рѐбер (u,v) и (v, w) называется включением последовательности.
Определение 8. Будем говорить, что два графа гомеоморфны, если они изо-
морфны или могут стать изоморфными в результате операций включения или слияния последовательностей.
Далее приведѐм без доказательства три критерия планарности графа.
Теорема 5 (Куратовский). Граф планарен тогда и только тогда, когда он не со-
держит подграфа, гомеоморфного графу K5 или K3,3 .
Определение 9. Будем говорить, что граф G1 стягивается к графу G2 , если граф G2 может быть получен из G1 с помощью нескольких операций отождествления вершин, соединѐнных рѐбрами.
Теорема 6 (Вагнер). Граф планарен тогда и только тогда, когда он не содер-
жит подграфа, стягиваемого к графу K5 или K3,3 .
84

Определение 10. Граф G называется двойственным к графу G , если сущест-
вует такое взаимно однозначное соответствие их рѐбер, что множество рѐбер графа G
является циклом тогда и только тогда, когда соответствующее множество рѐбер гра-
фа G является разрезом.
Теорема 7 (Уитни). Граф имеет двойственный граф тогда и только тогда, ко-
гда он планарен.
3.11. Алгоритм плоской укладки графа
|
|
|
Определение 1. Пусть вершина v графа G имеет степень d (v) k |
и инцидент- |
||||||||||||||||||||||||||
на рѐбрам (u1,v),...,(uk ,v) . Операцией удаления вершины v |
будем называть еѐ замену на |
|||||||||||||||||||||||||||||
висячие вершины v1,..., vk |
и замену рѐбер (u1,v),...,(uk ,v) |
на рѐбра (u1,v1),...,(uk ,vk ) . |
|
|||||||||||||||||||||||||||
|
|
|
Определение 2. Если после удаления вершины v графа G число компонент связ- |
|||||||||||||||||||||||||||
ности графа увеличивается, то v |
называется точкой сочленения. |
|
|
|
||||||||||||||||||||||||||
|
|
|
Определение 3. Связный граф, не содержащий точек сочленения, называется 2- |
|||||||||||||||||||||||||||
связным (двусвязным). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Определение 4. Пусть связный граф G содержит точку сочленения v , инцидент- |
|||||||||||||||||||||||||||
ную рѐбрам (u1,v),...,(uk ,v) , причѐм после удаления вершины v |
образуется t |
компонент связ- |
||||||||||||||||||||||||||||
ности. Будем считать, что рѐбра |
(u1,v1),...,(ui |
,vi ) |
принадлежат первой компоненте связно- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
сти, |
|
рѐбра |
|
(ui 1,vi |
1),...,(ui ,vi ) |
|
принадлежат |
|
второй |
|
компоненте |
и |
т.д., |
рѐбра |
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ui |
t 1 |
1,vi |
|
1),...,(uk ,vk ) |
принадлежат последней компоненте. Заменим вершины v1,...,vi |
на v1 , |
||||||||||||||||||||||||
|
|
t 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
вершины |
|
|
v |
1 |
,...,v |
на |
v2 |
и |
т.д., вершины |
v |
|
1 |
,...,v |
на |
vt . Далее, |
заменим |
рѐбра |
|||||||||||||
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
i |
|
|
k |
|
|
|
|
|
|
||
|
|
|
|
|
|
i |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
t 1 |
|
|
|
|
|
|
|
|
|
|
(u1,v1),...,(ui ,vi |
) |
на |
(u1,v1),...,(ui |
, v1) , рѐбра (ui |
1,vi 1),...,(ui ,vi |
) |
на (ui 1,v2 ),...,(ui ,v2 ) |
и т.д., |
||||||||||||||||||||||
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
2 |
2 |
|
1 |
|
2 |
|
|
рѐбра |
(u |
|
|
1 |
,v |
|
1 |
),...,(u ,v ) |
на |
(u |
|
1 |
,vt ),...,(u ,vt ) . Данную операцию будем называть разъе- |
|||||||||||||||||
|
|
|
i |
t 1 |
i |
|
|
k |
k |
|
i |
t 1 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
t 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
динением графа по точке сочленения v.
Определение 5. Пусть связный граф G разъединѐн по всем своим точкам сочле-
нения. Образовавшиеся компоненты связности будем называть блоками графа G .
Пример 1. Следующий граф G (рис.3.1) имеет точку сочленения 7.
3 |
4 |
|
|
2 |
|
5 |
|
|
|
7 |
|
1 |
|
|
6 |
Рис.3.1.
85

После разъединения графа G по этой точке сочленения граф распадѐтся на сле-
дующие блоки (рис.3.2).
3 |
4 |
2 |
5 |
7 |
9 |
|
8 |
1 |
6 |
Рис.3.2.
Пусть G – некоторый граф. Очевидно, если каждая компонента связности графа G
имеет плоскую укладку, то и весь граф G имеет плоскую укладку. Поэтому достаточно уметь находить плоскую укладку для связного графа G .
Если G – связный граф и G1,...,Gk – все его блоки и каждый блок имеет плоскую укладку, то и весь граф G имеет плоскую укладку. Поэтому можно предполагать, что G –
двусвязный граф.
|
|
|
Определение 6. Пусть имеется некоторая плоская укладка подграфа G графа |
||
|
|
будем называть связную компоненту в вершинно- |
G . Сегментом S относительно G |
||
порождѐнном подграфе |
|
, к которой присоединены все рѐбра, инцидентные |
V (G) \V (G) |
||
этой компоненте, и концы этих рѐбер. Сегментом также будем называть любое ребро графа G , не принадлежащее G , оба конца которого принадлежат G .
Определение 7. Вершину v сегмента S , принадлежащую контактной.
Определение 8. Допустимой гранью для сегмента S относительно подграфа G
будем называть грань графа G , содержащую все контактные вершины сегмента S .
Множество всех допустимых граней для сегмента S будем обозначать (S) .
Определение 9. Простую цепь L сегмента S , соединяющую две различные кон-
тактные вершины и не содержащую других контактных вершин, будем называть -
цепью.
Теперь опишем алгоритм плоской укладки графа G , который будем предполагать двусвязным. Заметим, что дерево не является двусвязным графом, поэтому граф G дол-
жен содержать цикл.
0.Выберем некоторый простой цикл C графа G и уложим его на плоскости:
положим .
G C
86

1. Найдѐм грани плоской укладки графа G и сегменты относительно G . Если множество сегментов пусто, то укладка построена. Конец.
Иначе перейдѐм к пункту 2.
2.Для каждого сегмента S определим множество (S) . Если существует сег-
мент S , для которого (S) , то граф G непланарен. Конец.
Иначе перейдѐм к пункту 3.
3. Если существует сегмент S , для которого имеется единственная допустимая грань , то возьмѐм этот сегмент и эту грань. Иначе выберем любой сегмент S и произ-
вольную допустимую грань этого сегмента.
4.Выберем произвольную -цепь L S сегмента S и поместим еѐ в грань ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
заменим G на G L и перейдѐм к пункту 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 2. Выясним, является ли следующий граф планарным: |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
9 |
|
10 |
|
|
|
11 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
2 |
3 |
|
4 |
5 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
8 |
7 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
Здесь |
n 11, m 21 . |
Неравенство |
m 3n 6 |
выполняется. |
Сначала в качестве |
|
||||||||||||||
G |
||||||||||||||||||||
возьмѐм следующий цикл графа G : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
2 |
3 |
|
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
7 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
Далее перечислим все сегменты графа G относительно |
|
|
|
|
|
|
||||||||||||||
G : |
|
|
|
|
|
|||||||||||||||
|
|
9 |
10 |
|
|
11 |
|
|
1 |
2 |
2 |
4 |
|
|||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
3 |
5 |
|
6 |
7 |
8 |
6 |
6 |
|
||||||||
|
|
|
|
S1 |
|
|
S2 |
|
|
S3 |
S4 |
S5 |
S6 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разбивает плоскость на две |
||||||
Контактные вершины обведены квадратом. Подграф G |
||||||||||||||||||||
грани 1 и 2 , которые являются допустимыми для каждого из сегментов S1,..., S6 . Поэто-
му возьмѐм первый сегмент и выберем в нѐм -цепь 1–9–2, которую уложим в грань 2 :
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
9 |
|
|||
|
|
|
|
||
8 |
7 |
|
|
6 |
|
87

Это будет граф G2 . Цикл 1–9–2 ограничивает новую грань 3 . Перечислим сегмен-
ты относительно G2 :
9 |
10 |
|
|
11 |
|
1 |
2 |
2 |
4 |
|||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
3 |
3 |
5 |
6 |
7 |
8 |
6 |
6 |
||||||||
|
|
S1 |
|
|
S2 |
|
S3 |
S4 |
S5 |
S6 |
||||||
Для каждого сегмента найдѐм множество допустимых граней:
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
2 |
1, 2 |
1, 2 |
1, 2 |
1, 2 |
1, 2 |
Для сегмента S1 существует только одна допустимая грань 2 . Берѐм |
-цепь 2– |
||||||
10–3 сегмента S1 и укладываем еѐ в грань 2 : |
|
|
|
||||
1 |
2 |
3 |
4 |
5 |
|
||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
9 |
10 |
|
||||
|
|
|
|
||||
8 |
7 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
Обозначим полученный подграф G3 |
. Перечислим сегменты относительно G3 |
|||||||||||||||
|
11 |
|
1 |
2 |
2 |
4 |
4 |
9 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
5 |
6 |
7 |
8 |
6 |
6 |
10 |
10 |
|
|||||||
|
S1 |
|
S2 |
S3 |
S4 |
S5 |
S6 |
S7 |
|
|||||||
Для каждого сегмента найдѐм множество допустимых граней:
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
S7 |
1, 2 |
1, 2 |
1, 2 |
1, 2 |
1, 2 |
2 |
2 |
Для сегмента S6 существует только одна допустимая грань 2 . Возьмѐм -цепь 4– 10 сегмента S6 и уложим еѐ в грань 2 :
1 |
2 |
|
3 |
4 |
5 |
||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
9 |
10 |
|||||
|
|
|
|||||
8 |
7 |
|
|
|
|
6 |
|
88
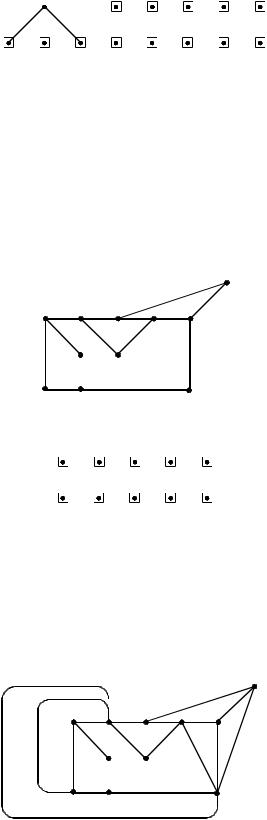
Полученный подграф обозначим G4 . Перечислим сегменты относительно G4 :
|
11 |
|
1 |
2 |
2 |
4 |
9 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
5 |
6 |
7 |
8 |
6 |
6 |
10 |
||||||
|
S1 |
|
S2 |
S3 |
S4 |
S5 |
S6 |
||||||
Для каждого сегмента найдѐм множество допустимых граней:
|
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
|
|
1 |
1, 2 |
1, 2 |
1, 2 |
1, 2 |
2 |
|
Далее сделаем сразу два шага. Уложим ребро (9,10) |
в грань 2 , а -цепь 3–11–5 |
||||||
сегмента S1 в грань 1 :
1 |
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
10 |
||
8 |
7 |
|
|
|
1
6
Остаются сегменты
1 |
2 |
|
|
2 |
4 |
6 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
6 |
|
|
8 |
6 |
11 |
||||||
|
S1 |
S2 |
|
S3 |
S4 |
S5 |
||||||
Находим допустимые грани: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
S2 |
|
S3 |
|
S4 |
|
|
S5 |
|
||
|
1, 2 |
1 |
|
1 |
|
2 |
|
|
1 |
|
||
Укладываем рѐбра (2,6), (2,8), (4,6), (6,11) в соответствующие грани:
|
|
|
|
|
|
|
|
11 |
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
9 |
10 |
|
|
||
8 7
Последний оставшийся сегмент 1–7 укладываем в единственную допустимую грань
2 . Таким образом, получим плоскую укладку графа G.
89

|
|
|
11 |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
9 |
10 |
||
8 |
7 |
|
|
|
Задачи
1. Нарисуйте плоские укладки графов пяти платоновых тел: тетраэдра, куба, окта-
эдра, додекаэдра, икосаэдра.
2. Докажите, что граф четырѐхмерного куба непланарен двумя способами:
а) найдя в нѐм подграф, гомеоморфный K5 ;
б) найдя подграф, гомеоморфный K3,3 .
Используя алгоритм плоской укладки графа, определите, являются ли следующие
графы планарными. Если нет, то найдите в них подграф, гомеоморфный K5 или K3, 3 .
3. |
|
||
|
4. |
||
|
|
|
|
|
|
|
|
5. |
|
6. |
|
||
|
|
|
90
