3.2. Проверка гипотезы о равенстве дисперсий

Рассмотрим две генеральные совокупности X и Y, распределенные по нормальному закону с дисперсиями и соответственно. Пусть по независимым выборкам и объемом n и m вычислены исправленные выборочные дисперсии и :

Примем для определенности, что . Можно ли считать, что выборочные дисперсии отличаются одна от другой только по случайности, присущей любым выборкам? Подобная гипотеза может возникать при сравнении точности двух одинаковых измерительных приборов или сравнении разброса параметров продукции двух заводов.

Проверить гипотезу о равенстве дисперсий и можно по критерию Фишера. В этом случае критерием F проверки нулевой гипотезы равенства дисперсий является отношение большей выборочной дисперсии к меньшей

.

При равенстве двух дисперсий (гипотеза справедлива) случайная величина F имеет распределение Фишера [3] и зависит от двух параметров (степеней свободы) k₁ = n – 1 и k₂ = m – 1. При альтернативной гипотезе критерий является правосторонним. При уровне значимости надо в таблице, приведенной в приложении 4, найти значение . Если наблюдаемое значение критерия

,

то гипотеза о равенстве дисперсий отвергается. В противном случае гипотеза не противоречит исходным данным и можно принять . В этом случае различие между выборочными дисперсиями и считается незначимым. В приложении 4 приведены величины только для значения 0,05. Критические точки при других уровнях значимости можно найти, например, в справочнике [2] или на странице сайта http://www.itl.nist.gov/div898/handbook/index.htm.

3.3. Проверка гипотезы о равенстве математических ожиданий

Подобная задача может возникнуть при проверке качества продукции, характеризуемым некоторым средним показателем (например, среднее время работы устройства, средний размер детали, среднее содержание компонентов смеси). И в этом случае исследуются две случайные величины (генеральные совокупности) X, Y с численными характеристиками и соответственно. Пусть из генеральных совокупностей X, Y извлечены независимые выборки , и для них вычислены выборочные средние:

.

Сначала рассмотрим случай, когда генеральные совокупности распределены по нормальному закону. При этом считаем, что статистическая гипотеза о равенстве дисперсий уже принята (см. параграф 3.2). Теперь проверим гипотезу о равенстве математических ожиданий и . Критерием проверки нулевой гипотезы равенства математических ожиданий (при альтернативной гипотезе ) может быть случайная величина

.

При равенстве математических ожиданий и (гипотеза справедлива) случайная величина имеет распределение Стьюдента [3] с числом степеней свободы .

После извлечения двух выборок случайная величина примет конкретное (наблюдаемое) значение . В таблице, приведенной в приложении 2, приведены критические точки распределения Стьюдента для различных уровней значимости . Данный критерий является двусторонним. Значит, если наблюдаемое значение критерия не попадает в интервал , то гипотеза о равенстве дисперсий отвергается. В противном случае гипотеза не противоречит исходным данным и можно считать, что . Тогда различие между выборочными математическими ожиданиями и считается незначительным (незначимым).

Рассмотрим также случай, когда две случайных величины имеют произвольное, может быть отличное от нормального, распределение. Но при этом выборки имеют достаточно большой объем (не менее 30 элементов каждая). Для проверки гипотезы о равенстве математических ожиданий введем центрированную и нормированную случайную величину

,

которая согласно центральной предельной теореме [3] при больших m и n распределена примерно по нормальному закону с параметрами , . Тогда, как было показано в параграфе 2.3, . При заданном уровне значимости значение критическое значение t, удовлетворяющее уравнению , можно найти в таблице приложения 1. Условие эквивалентно двойному неравенству

,

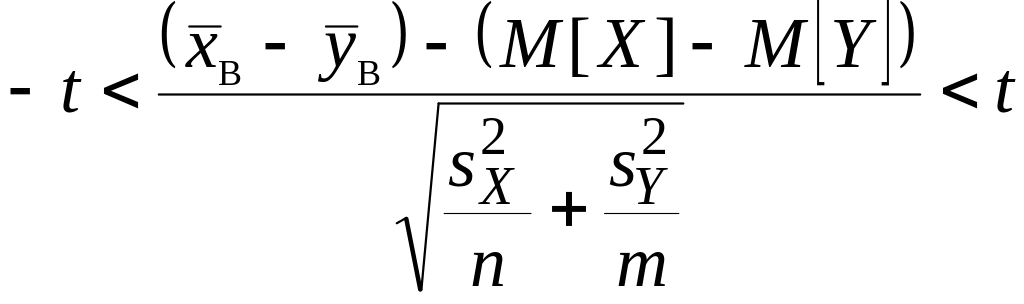которое можно записать в виде

.

Так как фактически проверяется равенство , то критерий проверки гипотезы можно сформулировать следующим образом: если 0 попадает в интервал

,

то гипотеза принимается.

Примеры проверки гипотез приведены в параграфе 3.7.