2.2. Точечные оценки математического ожидания и дисперсии

Законы распределения элементов выборки и генеральной совокупности одинаковы, следовательно, их математические ожидания равны: . В качестве точечной оценки естественно принять среднее арифметическое случайных величин :

.

Математическое ожидание обладает линейными свойствами [3], т.е. и . Поэтому

.

Следовательно, является несмещенной оценкой математического ожидания .

По теореме Чебышева [3] можно показать, что эта оценка является также состоятельной, а для нормального закона еще и эффективной.

Вычисленное для конкретной выборки выборочное среднее считается точечной оценкой параметра а, т.е.

.

Аналогично статистической оценкой дисперсии генеральной совокупности может быть выборочная дисперсия (см. параграф 1.4). Однако величина является смещенной оценкой [3], т.к.

.

Следует отметить, что при больших значениях , т.е. выборочная дисперсия является асимптотически несмещенной оценкой.

Исправленная выборочная дисперсия

становится несмещенной оценкой. Можно также показать, что такая точечная оценка будет состоятельной, а для нормального закона и асимптотически эффективной оценкой дисперсии.

В случае обработки сгруппированного вариационного ряда выборочная дисперсия, вычисленная с учетом поправки Шеппарда, также является несмещенной оценкой дисперсии.

2.3. Интервальные оценки математического ожидания нормального распределения

Случайная непрерывная величина Х подчинена нормальному закону распределения (закону Гаусса) с двумя параметрами a и , если ее плотность распределения имеет вид

.

Вид кривой плотности распределения , представленной на рис. 2.3.1, определяется конкретными значениями и [3].

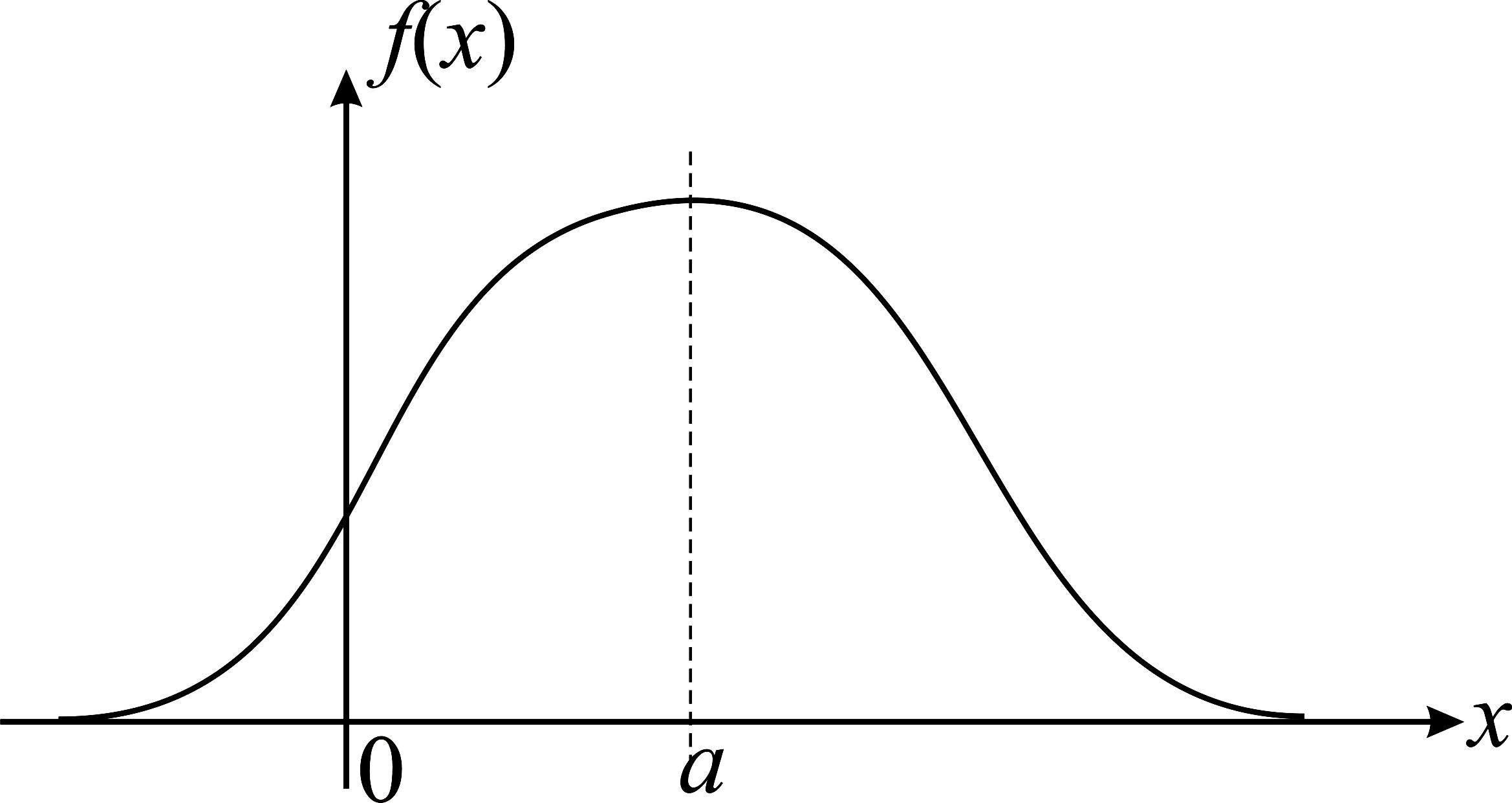
Рис. 2.3.1

Изменение величины параметра не изменяет формы нормальной кривой, но сдвигает ее вдоль оси х. Максимум функции f(x) достигается в точке а и равен . С возрастанием нормальная кривая становится более пологой, т. е. сжимается к оси x и растягивается вдоль нее. При уменьшении нормальная кривая стягивается к прямой x = a.

Математическое ожидание случайной величины с нормальным распределением М[Х] = а. Точка x = a называется центром распределения вероятностей, или центром рассеивания. Дисперсия нормального распределения случайной величины D[Х] = ².

Функция распределения нормального закона вычисляется по формуле

F(х) = .

График функции F(х) изображен на рис. 2.3.2.

Рис. 2.3.2

Распределение с параметрами и называется стандартным нормальным распределением. В этом случае функция распределения, которую принято обозначать Ф(х), имеет вид

.

На практике чаще используется функция Лапласа

.

Так как [3] , то в таблицах (см. приложение 1) можно приводить значения функции только для положительных значений аргумента. Производные функций и равны и

.

Таблицы значений функции также приведены в приложении 1.

Определив по таблице значение функции Лапласа, можно найти величину функции нормального распределения в любой точке:

.

Тогда вероятность попадания нормальной случайной величины X в интервал [х₁; х₂) вычисляется [3] по формуле

Р(х₁  Х < х₂) = .

Для нормального распределения также верна формула

.

Если случайная величина распределена по нормальному закону, то можно вывести формулы, позволяющие на основе выборки находить доверительные интервалы для математического ожидания а и среднеквадратичного отклонения .

Рассмотрим сначала случай, когда дисперсия известна, а оценить надо математическое ожидание а. Среднее арифметическое независимых случайных величин также распределено нормально [3]. При этом

, .

Если выполняется соотношение , то

.

Следовательно, зная , можно вычислить и определить надежность оценки математического ожидания , используя таблицу значений функции , приведенную в приложении 1. И, наоборот, значение t, удовлетворяющее уравнению , можно (при заданной надежности ) найти в таблице значений функции Лапласа. Затем, например, можно определить объем выборки , обеспечивающей заданные точность и надежность .

При точности оценки неравенство , эквивалентно двойному неравенству . Следовательно, с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр .

Если параметр распределения неизвестен, то для построения доверительного интервала надо сначала вычислить точечную оценку дисперсии s. Случайная величина

.

подчинена закону Стьюдента [3] и ее функция распределения не зависит от оцениваемого параметра а, а зависит только от объема выборки n. Параметр называется в статистике числом степеней свободы. Плотность вероятности распределения Стьюдента является четной функцией [3], следовательно, при выполняются равенства:

;

;

.

Тогда

.

Если обозначить через , то условие будет выполнено тогда, когда t является корнем уравнения . Зная величины уровня значимости и степени свободы _, значение , удовлетворяющее этому уравнению, можно найти в таблице приложения 2. Условие _{, эквивалентное неравенству} , задает доверительный интервал , покрывающий неизвестный параметр с надежностью . Очевидно, что при увеличении объема выборки n доверительный интервал уменьшается. При увеличении надежности оценки  уменьшается уровень значимости . По таблице приложения 2 видно, что в этом случае увеличивается значение t, а, следовательно, доверительный интервал становится больше.

При построении интервальной оценки среднеквадратичного отклонения также предполагается, что случайная величина Х подчинена нормальному закону распределения с параметрами a и . Пусть по результатам n испытаний вычислена точечная оценка дисперсии . Для того чтобы построить доверительный интервал для среднеквадратичного отклонения , рассмотрим

.

Распределение случайной величины называется [3] распределением («хи-квадрат»). Функция распределения такой величины не зависит от оцениваемого параметра , а зависит лишь от числа степеней свободы .

Рассмотрим соотношение

.

Обозначив , после несложных преобразований (при ) получим

или

.

Обозначая , получаем уравнение

.

Для распределения в приложении 3 приведены решения этого уравнения при различных значениях и k.

Итак, вычислив по выборке и найдя по таблице, имеем возможность записать искомый доверительный интервал, покрывающий значение с заданной надежностью :

, если ;

, если .

Отметим, что есть и другие способы построения доверительных интервалов [1]. В случае, например, можно доверительные интервалы находить по формулам:

;

;

Значение , удовлетворяющее уравнению , можно найти в приложении 1. Примеры расчета доверительных интервалов приведены в параграфе 2.4.