
- •Математическая статистика Учебное пособие
- •Введение
- •1. Описательная статистика
- •1.1. Выборка
- •1.2. Статистическое распределение выборки
- •1.3. Эмпирическая функция распределения
- •1.4. Числовые характеристики выборки
- •2. Статистические оценки параметров теоретического распределения
- •2.1. Точечные и интервальные оценки
- •2.2. Точечные оценки математического ожидания и дисперсии
- •2.3. Интервальные оценки математического ожидания нормального распределения
- •2.4. Примеры статистических расчетов
- •3. Проверка статистических гипотез
- •3.1. Статистические гипотезы
- •3.2. Проверка гипотезы о равенстве дисперсий
- •3.3. Проверка гипотезы о равенстве математических ожиданий
- •3.4. Критерии согласия
- •3.5. Критерий согласия Пирсона
- •3.6. Критерий согласия Колмогорова
- •3.7. Примеры проверки гипотез
- •Приложения
- •Для двусторонней критической области
- •Значения коэффициента q(, k)
- •Критические точки распределения χ2
- •Функция распределения k(t)
- •Содержание
- •Математическая статистика
- •190031, СПб., Московский пр., 9.
3.6. Критерий согласия Колмогорова
При любом критерии
согласия сравниваются две функции
распределения: эмпирическая
и предполагаемая теоретическая
.
Если расхождения между ними велики, то
гипотеза
о том, что функция распределения
генеральной совокупности имеет вид
,
отвергается. В критерии Колмогорова
степень расхождения оценивается
максимальной (при всех возможных
значениях х)
величиной разности опытной
и теоретической
функций. Рассмотрим случайную величина
![]() ,
где
,
где
![]() .
При справедливости гипотезы
и больших объемах выборки n
случайная величина Т
имеет функцию распределения близкую к
.
При справедливости гипотезы
и больших объемах выборки n
случайная величина Т
имеет функцию распределения близкую к
![]() ,
некоторые значения которой приведены
в приложении 5. Задав уровень значимости
,
можно по таблице найти значение
при котором
,
некоторые значения которой приведены
в приложении 5. Задав уровень значимости
,
можно по таблице найти значение
при котором
![]() .
Если в конкретной выборке Т
примет значение
.
Если в конкретной выборке Т
примет значение
![]() и при этом
и при этом
![]() ,
то гипотеза
о том, что функция распределения
генеральной совокупности равна
,
отвергается. Если
,
то гипотеза
о том, что функция распределения
генеральной совокупности равна
,
отвергается. Если
![]() ,
то статистические данные не противоречат
гипотезе
.
,
то статистические данные не противоречат
гипотезе
.
3.7. Примеры проверки гипотез
I.
Пусть по двум независимым выборкам
(объемом
![]() и
и
![]() соответственно), полученным из нормальных
генеральных совокупностей, вычислены
исправленные выборочные дисперсии
соответственно), полученным из нормальных
генеральных совокупностей, вычислены
исправленные выборочные дисперсии
![]() и
и
![]() .
Чтобы убедится в том, что различие между
.
Чтобы убедится в том, что различие между
![]() и
и
![]() несущественно (незначимо), проверим
нулевую гипотезу
о равенстве генеральных дисперсий.
Согласно критерию Фишера, прежде всего,
надо вычислить отношение большей
дисперсии к меньшей:
несущественно (незначимо), проверим
нулевую гипотезу
о равенстве генеральных дисперсий.
Согласно критерию Фишера, прежде всего,
надо вычислить отношение большей
дисперсии к меньшей:
 .
.
При конкурирующей
гипотезе
![]() критическая область является односторонней.
При уровне значимости
критическая область является односторонней.
При уровне значимости
![]() и степенях свободы
и степенях свободы
![]() и
и
![]() в таблице приложения 4 находим
в таблице приложения 4 находим
![]() .
Так как
.
Так как
![]() ,
то нет оснований отвергать гипотезу о
равенстве генеральных дисперсий и
различие между
и
незначимо.
,
то нет оснований отвергать гипотезу о
равенстве генеральных дисперсий и
различие между
и
незначимо.
II.
Пусть имеются две независимые выборки
из генеральных совокупностей X
и Y
объемом
![]() и
и
![]() соответственно. Для них вычислены
выборочные средние
соответственно. Для них вычислены
выборочные средние
![]() ;
;
![]() и исправленные выборочные дисперсии
и исправленные выборочные дисперсии
![]() ;
.
Проверим нулевую гипотезу
о равенстве генеральных средних, чтобы
убедиться в том, что различие между
величинами
;
.
Проверим нулевую гипотезу
о равенстве генеральных средних, чтобы
убедиться в том, что различие между
величинами
![]() и
и
![]() можно считать незначимым.
можно считать незначимым.
Значение t,
удовлетворяющее уравнению
,
находим по таблице приложения 1. При
уровне значимости
величина
![]() является приближенным решением этого
уравнения, так как
является приближенным решением этого
уравнения, так как
![]() .
При найденном значении t
вычисляем
.
При найденном значении t
вычисляем
![]() ;
;
![]() .
.
Так как 0 попадает в интервал (–0,15; 0,39) то гипотеза принимается.
III. Результаты 200 измерений некоторой физической величины представлены в таблице 3.7.1 сгруппированным вариационным рядом.
Таблица 3.7.1
Интервал |
[3; 4] |
(4; 5] |
(5; 6] |
(6; 7] |
(7; 8] |
(8; 9] |
(9; 10] |
(10; 11] |
|
3 |
7 |
26 |
56 |
64 |
30 |
12 |
2 |
Требуется с помощью критерия Пирсона проверить гипотезу о том, что генеральная совокупность распределена по нормальному закону.
Проверка нулевой гипотезы по критерию Пирсона состоит из нескольких этапов.
По выборке вычисляются точечные оценки математического ожидания
 и среднеквадратического отклонения
и среднеквадратического отклонения
 .
.В каждом промежутке определяются эмпирические частоты и теоретические вероятности.
Для данной выборки вычисляется наблюдаемое значение
 критерия Пирсона.
критерия Пирсона.
Задается уровень значимости и подсчитывается количество степеней свободы.
По таблице приложения 3 определяется значение
 .
.Если
 ,
то гипотеза
отвергается как маловероятная.
,
то гипотеза
отвергается как маловероятная.
1) Определив объем
выборки
![]() ,
вычисляем выборочное среднее
,
вычисляем выборочное среднее
![]() и несмещенную оценку среднеквадратического
отклонения
:
и несмещенную оценку среднеквадратического
отклонения
:
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таблица 3.7.2
Интервал |
|
(– ; 5] |
|
(5; 6] |
|
(6; 7] |
|
(7; 8] |
|
(8; 9] |
|
(9; ) |
|
Граница
|
|
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
|
|
|
10 |
|
26 |
|
56 |
|
64 |
|
30 |
|
14 |
|
|
|
|
– 1,66 |
|
– 0,87 |
|
– 0,075 |
|
0,72 |
|
1,51 |
|
|
|
– 0,5 |
|
– 0,45 |
|
– 0,31 |
|
– 0,03 |
|
0,26 |
|
0,43 |
|
0,5 |
|
|
0,05 |
|
0,14 |
|
0,28 |
|
0,29 |
|
0,17 |
|
0,07 |
|
|
|
10 |
|
28 |
|
56 |
|
58 |
|
34 |
|
14 |
|
|
|
0 |
|
2 |
|
0 |
|
6 |
|
4 |
|
0 |
|
|
|
0 |
|
0,14 |
|
0 |
|
0,62 |
|
0,47 |
|
0 |
|
2) Теперь, используя таблицу приложения 1, надо найти теоретические вероятности попадания варианты в каждый промежуток
,
и определить
![]()
Вычисления удобно проводить в таблице 3.7.2. Предварительно следует изменить таблицу 3.7.1, объединив первый столбец со вторым и седьмой столбец с восьмым, так как в крайних столбцах количество вариант меньше пяти.
Сначала в граничных точках вычисляем аргументы функции Лапласа. Например, для промежутка (7; 8] имеем
![]() ,
,
![]() .
.
По таблице приложения 1 вычисляем теоретическую вероятность попадания варианты в промежуток (7; 8]
![]() .
.
Функции
![]() является нечетной, следовательно,
является нечетной, следовательно,
![]() .
.
В последней строке
таблицы 3.7.2 помещены значения
![]() .
Для промежутка
[7; 8) эта величина принимает значение
.
Для промежутка
[7; 8) эта величина принимает значение
![]() .
.
3) Суммируя все
числа последней строки, получаем
![]() .
Полученное число необходимо сравнить
с величиной
.
.
Полученное число необходимо сравнить
с величиной
.
4) Выбираем
уровень значимости
.
Количество интервалов
![]() вариационного ряда, приведенного в
таблице 3.7.2, равно шести, следовательно,
число степеней свободы
вариационного ряда, приведенного в
таблице 3.7.2, равно шести, следовательно,
число степеней свободы
![]() .
.
5) В таблице
приложения 3 параметрам
![]() и
и
![]() соответствует значение
соответствует значение
![]() .
.
6)
![]() при выбранной надежности 0,95, следовательно,
отвергать гипотезу
оснований нет. Предположение о том, что
исследуемая физическая величина
распределена по нормальному закону с
параметрами
при выбранной надежности 0,95, следовательно,
отвергать гипотезу
оснований нет. Предположение о том, что
исследуемая физическая величина
распределена по нормальному закону с
параметрами
![]() ,
,
![]() ,
не противоречит результатам измерений.
,
не противоречит результатам измерений.
Следовательно, можно считать, что функция плотности вероятности изучаемой физической величины имеет вид (см. параграф 2.3)
 .
.
Значения функции
![]() приведены в таблице приложения 1, а
график
изображен на
рисунке 3.7.1 сплошной линией. Отдельные
точки на том же рисунке соответствуют
относительной частоте выборки
приведены в таблице приложения 1, а
график
изображен на
рисунке 3.7.1 сплошной линией. Отдельные
точки на том же рисунке соответствуют
относительной частоте выборки
![]() .
Очевидно, что теоретическое распределение
вполне согласуется с результатами
выборки.
.
Очевидно, что теоретическое распределение
вполне согласуется с результатами
выборки.

Рис. 3.7.1
IV. Проверить гипотезу , выдвинутую в предыдущей задаче, с помощью критерия Колмогорова.
Проверка нулевой гипотезы по критерию Колмогорова также состоит из нескольких этапов.
Вычисляются значения эмпирической
 и теоретической
функций распределения.
и теоретической
функций распределения.
Определяется наибольшее расхождение
 между этими функциями, т.е.
между этими функциями, т.е.

Вычисляется
 .
.Задается уровень значимости .
По таблице
 приложения 5 выбирается
приложения 5 выбирается
 ,
при котором
,
при котором
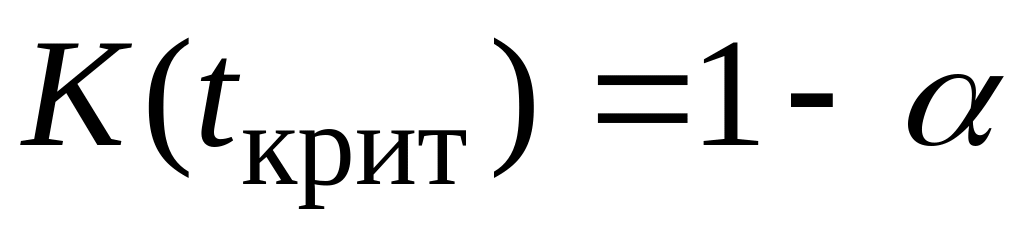 .
.Если
 ,
то гипотеза
отвергается как маловероятная.
,
то гипотеза
отвергается как маловероятная.
1) Во всех точках
![]() (см. таблицу 1.3.2) найдем разность
(см. таблицу 1.3.2) найдем разность
![]() двух функций распределения: эмпирической
двух функций распределения: эмпирической
![]() и предполагаемой теоретической
и предполагаемой теоретической
![]() при
при
![]() и
и
![]() .
Результаты вычислений представим в
виде таблицы 3.5.3.
.
Результаты вычислений представим в
виде таблицы 3.5.3.
Таблица 3.7.3
Интервал |
[3; 4] |
(4; 5] |
(5; 6] |
(6; 7] |
(7; 8] |
(8; 9] |
(9; 10] |
(10; 11] |
|
3 |
7 |
26 |
56 |
64 |
30 |
12 |
2 |
|
3 |
10 |
36 |
92 |
156 |
186 |
198 |
200 |
|
0,015 |
0,05 |
0,18 |
0,46 |
0,78 |
0,93 |
0,99 |
1 |
|
–2,46 |
–1,66 |
– 0,87 |
– 0,075 |
0,72 |
1,51 |
2,31 |
3,01 |
|
– 0,493 |
– 0,45 |
– 0,31 |
– 0,03 |
0,26 |
0,43 |
0,4896 |
0,499 |
|
0,007 |
0,05 |
0,19 |
0,47 |
0,76 |
0,93 |
0,99 |
1 |
|
0,008 |
0 |
0,01 |
0,01 |
0,02 |
0 |
0 |
0 |
Например, для
первого интервала, в котором
![]() ,
,
![]() .
.
По таблице приложения 1 вычисляем значения теоретической функции распределения в граничных точках
![]() .
.
Например, для первого интервала,
![]()
![]() .
.
Модуль разности
значений двух вычисленных функций
![]() записываем в последнюю строку таблицы.
записываем в последнюю строку таблицы.
2) Наибольшее число
последней строки расположено в пятом
столбце, поэтому принимаем
![]() .
.
3) С учетом объема
выборки
![]() находим значение, которое приняла
случайная величина Т
для данной выборки:
находим значение, которое приняла
случайная величина Т
для данной выборки:
![]() .
.
4) При уровне
значимости
значение функции распределения
Колмогорова
![]() должно равняться 0,95.
должно равняться 0,95.
5) В таблице значений
(см. приложение 5) в одиннадцатой строке
и шестом столбце расположено число
0,9505,
следовательно,
![]() .
.
6) При
![]() нет оснований отвергать гипотезу
.
нет оснований отвергать гипотезу
.
Можно считать, что функция распределения генеральной совокупности имеет вид
![]() .
.
График этой функции
изображен на рисунке 3.7.2 сплошной линией.
Отдельные точки на том же рисунке
соответствуют значениям эмпирической
функции распределения
![]() .
Очевидно, что теоретическое распределение
вполне согласуется с результатами
выборки.
.
Очевидно, что теоретическое распределение
вполне согласуется с результатами
выборки.

Рис. 3.7.2
В заключение
приведем критические значения
![]() и
и
![]() распределения Колмогорова для других
уровней значимости (
распределения Колмогорова для других
уровней значимости (![]() и
и
![]() соответственно).
соответственно).

